5.4: Derivadas de Funciones Trigonométricas

Las funciones sinx y cosx son periódicas, con periodo 2π. Has aprendido que la derivada de una función diferenciable da la pendiente de la línea tangente en un punto. Antes de continuar con esta lección, mire las curvas de función para las dos funciones, y vea si puede identificar algún punto donde sepa cuál será la derivada. Para cada función, ¿estos conjuntos de puntos se repiten a medida que x aumenta o disminuye? ¿Con qué frecuencia? ¿Se puede hacer una declaración general sobre las derivadas de las funciones trigonométricas?

---

Derivadas de Funciones Trigonométricas

Ahora queremos encontrar una expresión para la derivada de cada una de las seis funciones trigonométricas:

sin x	cos x	bronceado x
csc x	seg x	cuna x

Primero consideramos el problema de diferenciar sin x, utilizando la definición de la derivada.

\[ \displaystyle \frac{d}{dx}[sinx]=\lim_{h \to 0} \frac{sin(x+h)−sinx}{h} \nonumber\]

Desde

\[ sin(α+β)=sinαcosβ+cosαsinβ \nonumber\]

El derivado se convierte en

\[ \displaystyle \frac{d}{dx}[sinx]=\lim_{h \to 0} \frac{sinxcosh+cosxsinh−sinx}{h} \nonumber\]

\[ \displaystyle = \lim_{h \to 0} [sinx(\frac{cosh−1}{h})+cosx(\frac{sinh}{h})] \nonumber\]

\[ \displaystyle =−sinx⋅limh→0(1−coshh)+cosx⋅limh→0(sinhh) \nonumber\]

\[ =−sinx⋅(0)+cosx⋅(1) \nonumber\]

\[ =cosx \nonumber\]

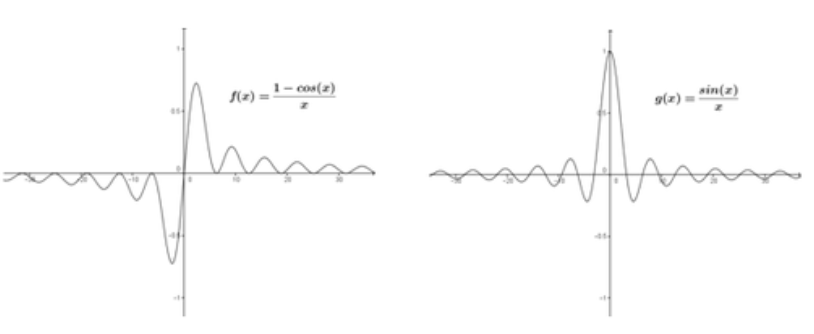
Veamos\[ \displaystyle \lim_{h\to0}\frac{1−cos(h)}{h} \nonumber\] y\[ \displaystyle \lim_{x \to 0} \frac{sin(h)}{h}\nonumber\] Si bien existen métodos analíticos que se pueden utilizar para evaluar estos dos límites, veamos los gráficos de funciones y los datos de tablas. A continuación se muestran las gráficas de las dos funciones y algunos datos de la tabla de la calculadora. La inspección de estos cerca de x=0 parece mostrar que los límites son:

\[ \displaystyle \lim_{x \to 0} \frac{cos(h)−1}{h}=0 \nonumber\]y\[ \displaystyle \lim_{h \to 0} \frac{sin(h)}{h}=1 \nonumber\]

Los resultados anteriores se pueden confirmar analíticamente.

CC BY-NC-SA

x (rad)	-0.001	-0.0001	0	0.0001	0.0001
f (x)	-0.0005	-0.00005	Error	0.00005	0.0005
g (x)	0.99999833	0.999999998	Error	0.999999998	0.99999833

Por lo tanto,

\[ \frac{d}{dx}[sinx]=cosx \nonumber\]

Se dejará como ejercicio para demostrar que\[ \frac{d}{dx}[cosx]=−sinx\]

A continuación se muestran las derivadas de las seis funciones trigonométricas.

\[ \frac{d}{dx} [sinx]= cosx \nonumber\]	\[ \frac{d}{dx} [cosx]= -sinx \nonumber\]	\[ \frac{d}{dx} [tanx]= sec^2x \nonumber\]
\[ \frac{d}{dx} [cscx]= -cscxcotx \nonumber\]	\[ \frac{d}{dx} [secx]= secxtanx \nonumber\]	\[ \frac{d}{dx} [cotx]= -csc^2x \nonumber\]

Tenga en cuenta que el argumento x para todas las funciones trigonométricas se mide en radianes.

Todas las derivadas pueden ser probadas por la definición de la derivada, pero las funciones recíprocas se pueden encontrar usando un método más simple. La prueba de\[ \frac{d}{dx}[tanx]=sec^2x \nonumber\] es la siguiente:

Desde

\[ tanx= \frac{sinx}{cosx} \nonumber\]

entonces

\[ \frac{d}{dx}[tanx]=\frac{d}{dx}[\frac{sinx}{cosx}] \nonumber\]

Usando la regla del cociente,

\[ =\frac{(cosx)(cosx)−(sinx)(−sinx)}{cos^2x} \nonumber\]

\[ =\frac{cos^2x+sin^2x}{cos^2x} \nonumber\]

\[=\frac{1}{cos2x} \nonumber\]

\[ =sec^2x\nonumber\]

---

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó si hay algún punto repetitivo para las derivadas de las funciones trigonométricas y de ser así, con qué frecuencia se repiten.

Primero, vea si puede identificar algún punto donde conozca la derivada de sinx y cosx: Cada función tiene dos lugares en el intervalo 0≤x≤2π donde la línea tangente tiene una pendiente de 0.

Para cada función, ¿estos conjuntos de puntos se repiten a medida que x aumenta o disminuye? Sí, estos 0 puntos de pendiente se repiten para cada función.

¿Con qué frecuencia? El par de 0 puntos de pendiente se repite con un periodo de 2π.

¿Se puede hacer una declaración general sobre las derivadas de las funciones trigonométricas? Debido a que los valores de la función se repiten cada período, la derivada de cada función en un punto específico también debe repetirse con el periodo 2π.

Ejemplo 2

Encuentra f′ (x) si f (x) =x ² cosx+sinx.

Usando la regla del producto y las fórmulas anteriores, obtenemos

\[ f′(x)=x^2(−sinx)+2xcosx+cosx \nonumber\]

\[ =−x^2sinx+2xcosx+cosx \nonumber\]

Ejemplo 3

Encuentra ^dy/_dx si\[ y=\frac{cosx}{1−tanx} \nonumber\] ¿Cuál es la pendiente de la línea tangente en\[x=π3?\nonumber\]

Usando la regla del cociente y las fórmulas anteriores, obtenemos

\[ \frac{dy}{dx}=\frac{(1−tanx)(−sinx)−(cosx)(−sec^2x)}{(1−tanx)^2} \nonumber\]

\[ =\frac{−sinx+tanxsinx+cosxsec^2x}{(1−tanx)^2} \nonumber\]

Para calcular la pendiente de la línea tangente, simplemente sustituimos\[ x=\frac{π}{3}\nonumber\]

\[ \frac{dy}{dx}|_{x=\frac{π}{3}}=\frac{−sin(\frac{π}{3})+tan(π3)sin(\frac{π}{3})+cos(\frac{π}{3})sec^2(\frac{π}{3})}{(1−tan(\frac{π}{3}))^2} \nonumber\]

Finalmente conseguimos que la pendiente sea aproximadamente

\[ \frac{dy}{dx}|_{x=\frac{π}{3}}=4.9 \nonumber\]

Ejemplo 4

Encuentra ^dy/_dx si\[ y=\frac{cotx}{sinx} \nonumber\]

\[ \frac{d}{dx}[\frac{cotx}{sinx}]=\frac{sinx\frac{dy}{dx}[cotx]−cotx\frac{dy}{dx}[sinx]}{sin^2x} \nonumber\]

Regla del cociente

\[ =\frac{sinx⋅[−csc^2x]−cotx⋅[cosx]}{sin^2x} \nonumber\]

Derivados trigonométricos

\[ =\frac{−sinx⋅[csc^2x+cot^2x]}{sin^2x} \nonumber\]

factor - sin x

\[ =−cscx⋅[1+cot^2x+cot^2x] \nonumber\]

simplificar y usar identidades trigonométricas

\[=−cscx⋅[1+2cot^2x] \nonumber\]

Por lo tanto,

\[ \frac{dy}{dx}=−cscx⋅[1+2cot^2x] \nonumber\]

---

Revisar

Para #1 -10, encuentra la derivada y′.

1. \[ y=xsinx+2 \nonumber\]
2. \[ y=x^2cosx−xtanx−1 \nonumber\]
3. \[ y=sin^2x \nonumber\]
4. \[ y=\frac{sinx−1}{sinx+1} \nonumber\]
5. \[ y=\frac{cosx+sinx}{cosx−sinx} \nonumber\]
6. \[ y=\frac{x^{0.5}}{tanx+2} \nonumber\]
7. \[ y=cscxsinx+x \nonumber\]
8. \[ y=\frac{secx}{cscx} \nonumber\]
9. Si y = csc x, encuentra y′ (^π/₆).
10. y=x ⁵ cos (x)?
11. ¿Cuál es la derivada de x ² csc (x)?
12. ¿Cuál es la derivada de csc (x) tan (x)?
13. Utilice la regla del cociente para verificar que la derivada de sec (x) es sec (x) tan (x).
14. ¿Cuál es la derivada de cot (^π/₂ −x)?
15. ¿Cuál es la derivada de csc ² (x) −cot ² (x)?

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.7.

---

El vocabulario

Término	Definición
derivado	La derivada de una función es la pendiente de la línea tangente a la función en un punto dado de la gráfica. Las notaciones para derivadas incluyen f′ (x), dydx, y′, dfdx y\ frac {df (x)} {dx}.

---

Recursos adicionales

PLIX: Jugar, Aprender, Interactuar, Explorar - Derivada del pecado (x)

Video: La derivada de seno y coseno

Práctica: Derivadas de funciones trigonométricas

Mundo real: visión de rayos X