8.1: Extrema Absoluta y Optimización
- Page ID
- 106031
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En este punto, se sabe analizar una función para encontrar sus mínimos y máximos utilizando la primera y segunda derivadas. Encontrar la solución a algún problema del mundo real (como en finanzas, ciencia e ingeniería) a menudo implica un proceso de encontrar el máximo o mínimo de una función dentro de una región aceptable de valores. Este tipo de problema es un problema de optimización, y la solución que es el valor máximo o mínimo de la función en la región es la solución óptima. Configurar el problema de optimización es el primer paso importante. Mira si puedes configurar (pero no resolver) este problema: ¿Qué dimensiones minimizarán la cantidad de metal requerida para construir un tanque de almacenamiento de volumen 1000 m3 que tenga la forma de un cilindro circular derecho y que tenga una parte superior que sea un hemisferio?
Optimización
En conceptos anteriores, discutimos métodos para encontrar máximos y mínimos (extremos) de funciones, y estos métodos se utilizan para resolver problemas de optimización. Supongamos que f es continuo en un intervalo cerrado [a, b]. Recordemos que podemos encontrar el mínimo y máximo absoluto de una función f que es continua en un intervalo cerrado [a, b] de la siguiente manera:
- Encontrar los valores de f para cada valor crítico en (a, b);
- Encontrar los valores de la función f en los puntos finales de [a, b];
- El máximo absoluto será el mayor valor de los números encontrados en 1 y 2; el mínimo absoluto será el número más pequeño.
Sin embargo, los problemas del mundo real a menudo imponen restricciones que deben tenerse en cuenta para encontrar la solución óptima.
Tome una empresa que fabrica llantas de bicicleta de alta calidad tanto para ciclistas recreativos como de carreras. El número de llantas que vende la compañía es función del precio cobrado y puede modelarse por la fórmula\( T(x)=−x^3+36.5x^2+50x+250 \nonumber\), donde x es el precio que se cobra por cada llanta en dólares. ¿A qué precio se vende el número máximo de llantas? ¿Cuántas llantas se venderán a ese precio máximo?
En este problema de optimización, estamos tratando de encontrar el valor máximo de T (x). T (x) es la ecuación primaria que se optimizará. Primero veamos una gráfica de la función del neumático y hagamos algunas observaciones. Establezca los rangos de ventana de visualización en su calculadora gráfica en [-10, 50] para x y [-500, 10000] para y.
La gráfica debe aparecer de la siguiente manera:
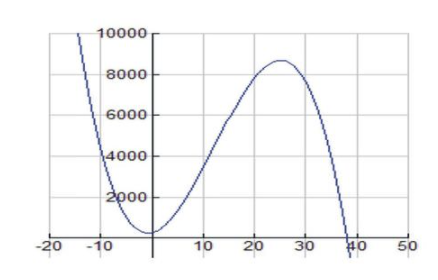
CC BY-NC-SA
Primero notamos que como se trata de una aplicación de la vida real, ambas cantidades, x y T (x), son positivas o de lo contrario el problema no tiene sentido. Estas condiciones, junto con el hecho de que el cero de T (x) se ubica en x=37.9, sugieren que el dominio real de esta función es 0<x≤37.9. Este dominio restringido, al que nos referimos como un dominio factible, ilustra una característica común de los problemas de optimización: que las condiciones de la vida real de la situación en estudio dictan los valores del dominio.
Podemos usar la gráfica de la calculadora o usar las Pruebas de Primera y Segunda Derivada para encontrar los máximos y mínimos absolutos en el intervalo cerrado [0, 37.9].
|
1 st Derivada \[ f′(x)=−3x^2+73x+50 \nonumber\] |
f′ (x) =0: a\(x=− \frac{2}{3} \nonumber\)... no en dominio; a x=25... en el dominio. |
|
2 º Derivada \[ f′′(x)=−6x+73 \nonumber\] |
f′′ (25) =23 Hay un máximo de función en x=25. |
Vemos que la función alcanza un máximo absoluto en x=25 en el punto (25, 8687.5). Entonces, cobrar un precio de 25 dólares resultará en la venta de un total de 8687 llantas.
En muchos problemas de optimización, se debe utilizar una ecuación secundaria (o más de una) para reducir el número de variables en la ecuación primaria antes de iniciar el procedimiento de optimización (uso de una calculadora gráfica; aplicación de pruebas derivadas).
Supongamos que Mary desea hacer una pluma rectangular al aire libre para su mascota chihuahua. A ella le gustaría que la pluma encierra un área en su patio trasero con uno de los lados del rectángulo hecho por el costado de la casa de María como se indica en la siguiente figura. Si tiene 90 pies de esgrima para trabajar, ¿qué dimensiones de la pluma resultarán en el área máxima?
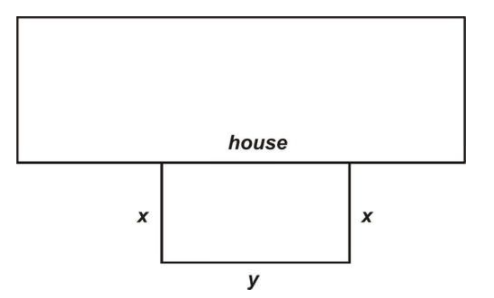
CC BY-NC-SA
Las dimensiones de la pluma son x e y en la figura. La ecuación primaria es la función que modela el área, A, de la pluma. Deseamos maximizar:
\[ A=xy \nonumber\]
La ecuación secundaria proviene de la información relativa a la esgrima con la que María tiene que trabajar. En particular,
\[ 2x+y=90 \nonumber\]
Resolviendo para y tenemos
\[ y=90−2x \nonumber\]
Ahora sustituimos en la ecuación primaria para obtener:
\( A=xy=x(90−2x) \nonumber\), o
\( A(x)=−2x^2+90x \nonumber\)
Siempre es útil ver la gráfica de la función a optimizar. Establezca los rangos de ventana de visualización en su calculadora gráfica en [-10, 100] para x y [-500, 1200] para y. La gráfica debe aparecer de la siguiente manera:
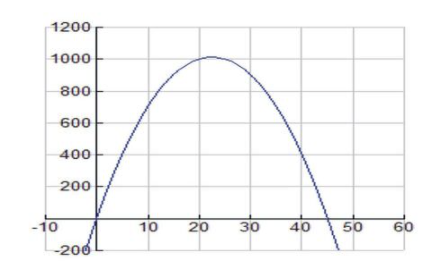
CC BY-NC-SA
El dominio factible de esta función es 0<x<45, lo que tiene sentido porque si x es de 45 pies, entonces la cifra será dos vallas de 45 pies de largo que se alejan de la casa con 0 pies para el ancho y.
Podemos encontrar la solución usando la calculadora gráfica, y/o las Pruebas de Primera y Segunda Derivada y el método para encontrar máximos y mínimos absolutos en un intervalo cerrado (en este problema, [0, 45]).
|
1 st Derivada A′ (x) =−4x+90 |
A′ (x) =0: a x=22.5... en el dominio. |
|
2 º Derivada A′′=−4 |
A′′=−4 Hay un máximo de función en x=22.5. |
Vemos que la función alcanza un máximo absoluto en x=22.5 en el punto (22.5, 1012.5).
Entonces las dimensiones de la pluma deben ser x=22.5, e y=45; con esas dimensiones, la pluma encerrará un área de 1012.5 ft2.
Problemas de optimización que involucran formas geométricas realmente ayudan a ilustrar el proceso de resolución de problemas. Aquí hay otro:
Cierta marca de limonada vende su producto en latas de aluminio de 16 onzas que contienen 473 ml (1 ml=1 cm3). Encuentra las dimensiones de la lata cilíndrica que utilizará la menor cantidad de aluminio.
Necesitamos desarrollar la fórmula para la superficie de la lata. Esta consiste en las áreas superior e inferior, cada una\( πr^2 \nonumber\), y la superficie del costado,\( 2πrh \nonumber\) (producto de la circunferencia de la parte superior y la altura de la lata). De ahí que la ecuación primaria es
\[ A=2πr^2+2πrh \nonumber\].
Observamos que nuestros dos dominios factibles requieren\(r,h>0 \nonumber\).
Para reducir el número de variables en la ecuación primaria, necesitamos una ecuación secundaria que nos dé una relación entre r y h. Observamos que el volumen para un cilindro circular viene dado por\( V=πr^2h \nonumber\), lo que proporciona una relación entre r y h. La ecuación secundaria es:
\[ h= \frac{V}{πr^2}= \frac{473}{πr^2} \nonumber\]
Sustituimos esta expresión por h en la ecuación primaria para obtener:
\( A(r)=2πr^2+2πr( \frac{473}{πr^2}) \nonumber\), o
\[ A(r)=2πr^2+\frac{946}{r} \nonumber\].
A continuación se muestra la gráfica de la función A (r):
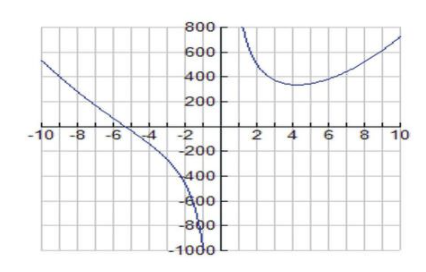
CC BY-NC-SA
El dominio factible es r>0.
| 1 st Derivada | \[ A′(r)=4πr− \frac{946}{r^2} \nonumber\] |
A′ (r) =0: a\( r= \frac{946}{4π}^{\frac{1}{3}}≈4.22 \nonumber\) cm... en el dominio. |
| 2 º Derivada | \( A′′(r)=4π+ \frac{1892}{r^3} \nonumber\) |
A′′ (r) >0 para r>0 Hay una función mínima a r≈4.22 cm. |
De ahí que tengamos una superficie mínima de 996.2 cm2 cuando r≈9.06 cm y h≈8.44 cm.
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó qué dimensiones minimizarán la cantidad de metal requerida para construir un tanque de almacenamiento de volumen 1000 m3 que tiene la forma de un cilindro circular derecho y tiene una parte superior que es un hemisferio.
El volumen del tanque consiste en el volumen de un ciclínder y el volumen de un hemisferio. El volumen se puede expresar como:\( V=πr^2h+ \frac{1}{2}( \frac{4}{3}πr^3)=1000 \nonumber\) donde r es el radio del tanque (en metros), y h es la altura del ciclínder (en metros).
Te gustaría minimizar la cantidad de metal utilizado, lo cual es lo mismo que pedir minimizar el área del tanque. Esta debería ser la declaración del problema de optimización.
El área se puede expresar como:\( A=2πrh+ \frac{1}{2}(4πr^2) \nonumber\). Debido a que hay dos variables, r y h, deberíamos hacer h a función r, es decir, h (r), usando la ecuación para V.
\ [h (r) =\ frac {1000} {πr^2} −\ frac {2} {3} r\ nonumber\)
La declaración del problema de optimización es entonces:
\( \frac{dA}{dr}=0= \frac{d}{dr}[2πrh(r)+ \frac{1}{2}(4πr^2)]=2π[h(r)+r \frac{dh}{dr}+2r] \nonumber\), o
\[ h(r)+r \frac{dh}{dr}+2r=0 \nonumber\].
El siguiente paso es resolver el problema de optimización para ver si hay una solución que tenga sentido. ¿Lo puedes hacer?
Ejemplo 2
Se construirá un contenedor de almacenamiento con una base rectangular, lados rectangulares y abierto en la parte superior. Su ancho es de 4 metros y su volumen es de 36 metros cúbicos. Si construir el contenedor cuesta $10/metros cuadrados para la base y $5 metros cuadrados para los lados, ¿cuál es el costo del contenedor menos costoso? ¿Cuáles son sus dimensiones?
Deje que las dimensiones de la papelera sean l largo, ancho w y alto h. Tenga en cuenta que w=4 metros.
La ecuación primaria es la función que modela el costo, C, del bin. Deseamos minimizar:
\[ C=10lw+5[2lh+2wh]=10[lw+lh+wh]=10[4l+lh+wh] \nonumber\]
La ecuación secundaria proviene de la información relativa al volumen del bin:
\[ V=lwh=4lh=36 \nonumber\]
Usando la ecuación secundaria en la ecuación primaria:
\[ C=10[4l+lh+wh]=10[4l+\frac{36}{4}+\frac{36}{l}]=40[l+2.25+\frac{9}{l}] \nonumber\]
Podemos encontrar la solución usando las Pruebas de Primera y Segunda Derivada y el método para encontrar máximos y mínimos absolutos en un intervalo cerrado (en este problema, [0, 45]).
|
1 st Derivada |
\[ C′(l)=40(1−\frac{9}{l^2}) \nonumber\] |
C′ (l) =0: a l=3 (en el dominio) y l=−3 (no en el dominio). |
|
2 º Derivada |
\[ C′′(l)=\frac{720}{l^3} \nonumber\] |
C′′ (3) ≈26.7. La función de costo es cóncava hacia arriba. Hay una función mínima en l=3. |
Entonces las dimensiones de la papelera son: l=3 metros, w=4 metros, y h=3 metros.
El costo para construir el bin: C (3) =$40 (3+2.25+3) =$330.
Revisar
Para #1 -4, encuentra los valores máximos absolutos y mínimos absolutos, si existen.
- \( f(x)=2x^2−6x+6 \mbox{ on } [0, 5] \nonumber\)
- \( f(x)=x^3+3x^2 \mbox{ on } [-2, 3] \nonumber\)
- \( f(x)=3x^{\frac{2}{3}}−6x+x \mbox{ on } [1, 8] \nonumber\)
- \( f(x)=x^4−x^3 \mbox{ on } [-2, 2] \nonumber\)
- Encuentra las dimensiones de un rectángulo que tenga área\( 2000 ft^2 \nonumber\) cuyo perímetro sea lo más pequeño posible.
- Encuentra dos números cuyo producto sea 50 y cuya suma sea mínima.
- John está disparando una básquetbol desde media cancha. Se encuentra aproximadamente a 45 pies desde la línea de media cancha hasta el aro. La función\( s(t)=−0.025x^2+x+15 \nonumber\) modela la altura de la básquetbol sobre el suelo s (t) en pies, cuando está a t pies del aro. ¿A cuántos metros de John llegará la pelota a su altura más alta? ¿Cuál es esa altura?
- La altura de un cohete modelo t segundos en vuelo viene dada por la fórmula\( h(t)=−13t^3+4t^2+25t+4 \nonumber\).
- ¿Cuánto tiempo tardará el cohete en alcanzar su altura máxima?
- ¿Cuál es la altura máxima a la que alcanzará el cohete?
- ¿Cuánto durará el vuelo?
- Mostrar que de todos los rectángulos de un perímetro dado, el rectángulo con mayor área es un cuadrado.
- Mostrar que de todos los rectángulos de un área dada, el rectángulo con el perímetro más pequeño es un cuadrado.
- Eduardo quiere construir una barda que proteja su jardín rectangular de jitomates de las diversas criaturas hambrientas que deambulan por el paisaje. Él compra 100 pies de barda. ¿Cuáles deberían ser las dimensiones del jardín de tomate si se quiere tener el área máxima que puede contener 100 pies de barda?
- Hans ha sido desafiado a encontrar dos números no negativos cuya suma es 36 para que el producto de los dos números sea máximo. ¿Cómo debe proceder?
- Lucía necesita encontrar dos números no negativos cuyo producto sea 25 para que se minimice la suma de uno más el cuadrado del otro, a fin de ganar membresía a un club. ¿Qué números busca?
- Esmeralda quiere encerrar un campo con una barda rectangular para evitar que sus cabras se escapen. Un lado del campo está contra un edificio, por lo que no requerirá cercado. Tiene 50 pies de material de esgrima. ¿Cuáles son las dimensiones del área máxima que puede cercar?
- ¿Qué punto de la gráfica de la función\( y=\sqrt{x} \nonumber\) está más cerca del punto (1, 0)?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.9.
vocabulario
| Término | Definición |
|---|---|
| dominio factible | El dominio factible es el subconjunto del dominio de la función primaria que se puede utilizar. Este dominio restringido está determinado por las restricciones del problema de optimización. |
| valor óptimo | Un valor o solución óptima es la mejor solución al problema de optimización. |
| optimización | Un problema de optimización es un problema de encontrar la mejor solución a un problema a partir de todas las soluciones factibles. |
| ecuación primaria | La ecuación primaria de un problema de optimización es la función o ecuación para la que se busca el valor o solución óptima. |
| ecuación secundaria | Una ecuación secundaria es una de las ecuaciones utilizadas para relacionar variables del problema y reducir el número de variables en la ecuación primaria. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Optimización: Construyendo la caja más grande
Video: Concepto y Ejemplo de Optimización
Práctica: Extrema Absoluta y Optimización
Mundo real: Mantener las luces encendidas

