1.6: La curva de posibilidades de producción

Modelos económicos

Los economistas utilizan modelos económicos para demostrar gráficamente los conceptos y teorías que desarrollan para explicar el comportamiento humano y la toma de decisiones.

Los factores de producción de una economía son escasos; no pueden producir una cantidad ilimitada de bienes y servicios. Una curva de posibilidades de producción es una representación gráfica de las combinaciones alternativas de bienes y servicios que una economía puede producir. Ilustra el modelo de posibilidades de producción. Al trazar la curva de posibilidades de producción, asumiremos que la economía sólo puede producir dos bienes y que las cantidades de factores de producción y la tecnología de que dispone la economía son fijas.

Generalizaciones Universales

• Los economistas realizan investigaciones evaluando fuentes; recopilando, analizando y sintetizando información; y comunicando conclusiones sustentadas en evidencia.
• Una curva de posibilidades de producción es una herramienta utilizada por los economistas para demostrar las compensaciones asociadas con la asignación de recursos.

Preguntas Orientadoras

1. ¿Qué se puede aprender al examinar una curva de posibilidades de producción?
2. ¿Cómo puede una curva de posibilidades de producción ayudar a los consumidores y productores a tomar mejores decisiones económicas?

Construyendo una curva de posibilidades de producción

Para construir una curva de posibilidades de producción, comenzaremos con el caso de una firma hipotética, Alpine Sports, Inc., fabricante especializado de equipos deportivos. Christie Ryder comenzó el negocio con una sola instalación de producción de esquí cerca de la estación de esquí de Killington en el centro de Vermont. Las ventas de esquís crecieron y también vio aumentar la demanda de tablas de snowboard, especialmente después de que los eventos de competencia de snowboard se incluyeron en los Juegos Olímpicos de Invierno de 2002 en Salt Lake City. Añadió una segunda planta en un pueblo cercano. La segunda planta, aunque más pequeña que la primera, fue diseñada para producir tablas de snowboard así como esquís. También modificó la primera planta para que pudiera producir tanto tablas de snowboard como esquís. Dos años después agregó una tercera planta en otro pueblo. Si bien es incluso más pequeña que la segunda planta, la tercera fue diseñada principalmente para la producción de snowboard pero también podría producir esquís.

Podemos pensar en cada una de las tres plantas de la Sra. Ryder como una economía en miniatura y analizarlas utilizando el modelo de posibilidades de producción. Suponemos que los factores de producción y tecnología disponibles para cada una de las plantas operadas por Alpine Sports no han cambiado.

Supongamos que la primera planta, Planta 1, puede producir 200 pares de esquís al mes cuando produce solo esquís. Cuando se dedica únicamente a las tablas de snowboard, produce 100 tablas de snowboard al mes. También puede producir esquís y tablas de snowboard simultáneamente.

La tabla de [Figura 1 - Una curva de posibilidades de producción] da tres combinaciones de esquís y tablas de snowboard que Plant 1 puede producir cada mes. La combinación A implica dedicar la planta completamente a la producción de esquí; la combinación C significa trasladar todos los recursos de la planta a la producción de snowboard; la combinación B implica la producción de ambos productos. Estos valores se trazan en una curva de posibilidades de producción para la Planta 1. La curva es una línea recta inclinada hacia abajo, lo que indica que existe una relación lineal negativa entre la producción de los dos bienes.

Ni los esquís ni las tablas de snowboard son una variable independiente o dependiente en el modelo de posibilidades de producción; podemos asignar uno al eje vertical o al eje horizontal. Aquí, hemos colocado el número de pares de esquís producidos por mes en el eje vertical y el número de tablas de snowboard producidas por mes en el eje horizontal.

La pendiente negativa de la curva de posibilidades de producción refleja la escasez de capital y mano de obra de la planta. Producir más tablas de snowboard requiere desplazar los recursos de la producción de esquí y, por lo tanto, producir menos esquís. Producir más esquís requiere desplazar los recursos de la producción de snowboard y, por lo tanto, producir menos tablas de snowboard.

La pendiente de la curva de posibilidades de producción de la Planta 1 mide la tasa a la que Alpine Sports debe renunciar a la producción de esquí para producir tablas de snowboard adicionales. Debido a que la curva de posibilidades de producción para la Planta 1 es lineal, podemos calcular la pendiente entre dos puntos cualesquiera de la curva y obtener el mismo resultado. Entre los puntos A y B, por ejemplo, la pendiente es igual a −2 pares de esquís/snowboard (equivale a −100 pares de esquís/50 tablas de snowboard). (A muchos estudiantes se les ayuda cuando se les dice que lean este resultado como “−2 pares de esquís por tabla de snowboard”). Obtenemos el mismo valor entre los puntos B y C, y entre los puntos A y C.

[Figura 1 - Una curva de posibilidades de producción]

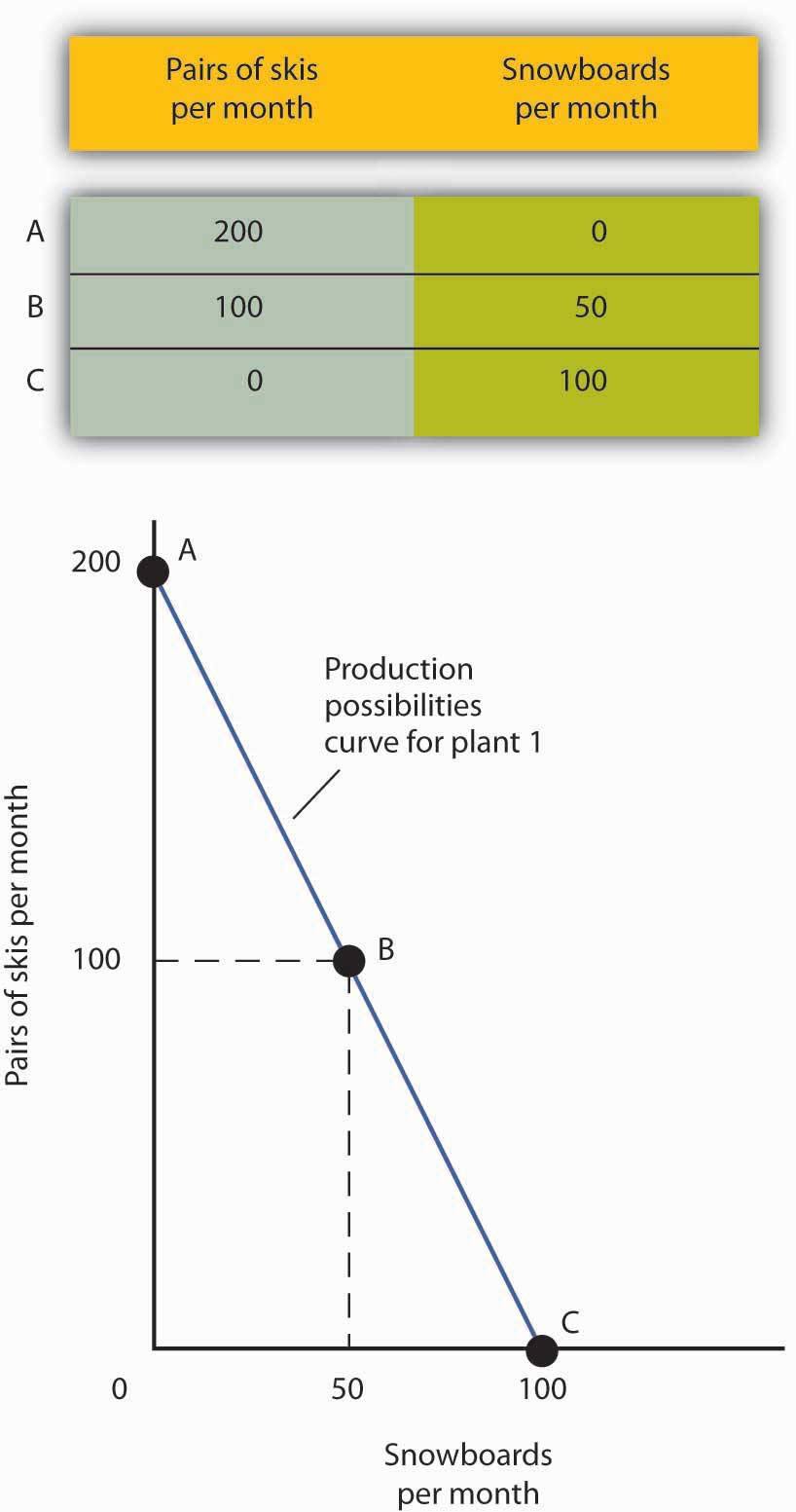
En la tabla se muestran las combinaciones de pares de esquís y tablas de snowboard que Plant 1 es capaz de producir cada mes. Estos también se ilustran con una curva de posibilidades de producción. Observe que esta curva es lineal.

Videos: Curva de posibilidades de producción y desplazamiento de la curva de posibilidades de producción

Antes de continuar con un examen más profundo de las posibilidades de producción de Alpine Sports, vea los videoclips a continuación para obtener una comprensión más clara de los conceptos básicos de la curva de posibilidades de producción:

Para ver más claramente esta relación, examine [Figura 2 - La pendiente de una curva de posibilidades de producción]. Supongamos que la Planta 1 está produciendo 100 pares de esquís y 50 tablas de snowboard al mes en el punto B. Ahora considere qué pasaría si la Sra. Ryder decidiera producir 1 snowboard más al mes. El segmento de la curva alrededor del punto B se magnifica en [Figura 2 - La pendiente de una curva de posibilidades de producción]. La pendiente entre los puntos B y B′ es de −2 pares de esquís/snowboard. Producir 1 tabla de snowboard adicional en el punto B′ requiere renunciar a 2 pares de esquís. Podemos pensar en esto como el costo de oportunidad de producir una tabla de snowboard adicional en la Planta 1. Este costo de oportunidad equivale al valor absoluto de la pendiente de la curva de posibilidades de producción.

[Figura 2 - La pendiente de una curva de posibilidades de producción]

La pendiente de la curva de posibilidades de producción lineal en [Figura 1 - Una curva de posibilidades de producción] es constante; es de −2 pares de esquís/snowboard. En la sección de la curva que se muestra aquí, la pendiente se puede calcular entre los puntos B y B′. Ampliar la producción de snowboard a 51 tablas de snowboard por mes de 50 tablas de snowboard al mes requiere una reducción en la producción de esquí a 98 pares de esquís por mes de 100 pares. La pendiente equivale a −2 pares de esquís/snowboard (es decir, debe renunciar a dos pares de esquís para liberar los recursos necesarios para producir una tabla adicional de snowboard). Para cambiar de B′ a B″, Alpine Sports debe renunciar a dos pares más de esquís por tabla de snowboard. El valor absoluto de la pendiente de una curva de posibilidades de producción mide el costo de oportunidad de una unidad adicional del bien en el eje horizontal medido en términos de la cantidad del bien en el eje vertical que debe olvidarse.

El valor absoluto de la pendiente de cualquier curva de posibilidades de producción equivale al costo de oportunidad de una unidad adicional del bien en el eje horizontal. Es la cantidad del bien en el eje vertical que se debe renunciar para liberar los recursos requeridos para producir una unidad más del bien en el eje horizontal. Haremos uso de este importante hecho a medida que continuemos nuestra investigación sobre la curva de posibilidades de producción.

[Figura 3 - Posibilidades de Producción en Tres Plantas] muestra curvas de posibilidades de producción para cada una de las tres plantas de la firma. Cada una de las plantas, si se dedicaba completamente a las tablas de snowboard, podría producir 100 tablas de snowboard. Las plantas 2 y 3, si se dedican exclusivamente a la producción de esquí, pueden producir 100 y 50 pares de esquís al mes, respectivamente. La exhibición da las pendientes de las curvas de posibilidades de producción para cada planta. El costo de oportunidad de un snowboard adicional en cada planta equivale a los valores absolutos de estas pendientes (es decir, el número de pares de esquís que se deben renunciar por tabla de snowboard).

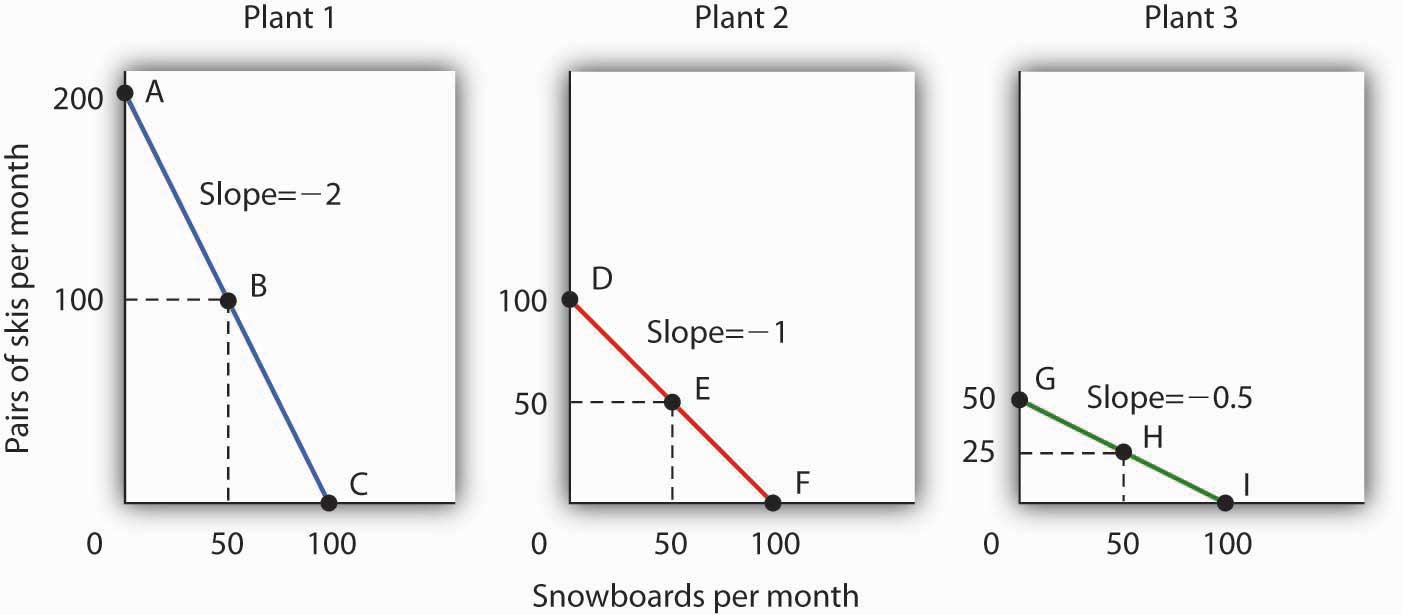[Figura 3 - Posibilidades de producción en tres plantas]

Las pendientes de las curvas de posibilidades de producción para cada planta difieren. Cuanto más pronunciada sea la curva, mayor será el costo de oportunidad de una tabla de snowboard adicional. Aquí, el costo de oportunidad es más bajo en la Planta 3 y mayor en la Planta 1.

La exhibición da las pendientes de las curvas de posibilidades de producción para cada una de las tres plantas de la firma. El costo de oportunidad de una tabla de snowboard adicional en cada planta equivale a los valores absolutos de estas pendientes. De manera más general, el valor absoluto de la pendiente de cualquier curva de posibilidades de producción en cualquier punto da el costo de oportunidad de una unidad adicional del bien en el eje horizontal, medido en términos del número de unidades del bien en el eje vertical que deben olvidarse.

Cuanto mayor sea el valor absoluto de la pendiente de la curva de posibilidades de producción, mayor será el costo de oportunidad. La planta para la que el costo de oportunidad de una tabla de snowboard adicional es la planta con la curva de posibilidades de producción más pronunciada; la planta para la que el costo de oportunidad es más bajo es la planta con la curva de posibilidades de producción más plana. La planta con el menor costo de oportunidad de producir tablas de snowboard es la Planta 3; su pendiente de −0.5 significa que la Sra. Ryder debe renunciar a medio par de esquís en esa planta para producir una tabla de snowboard adicional. En la Planta 2, debe renunciar a un par de esquís para ganar una tabla de snowboard más. Ya hemos visto que un snowboard adicional requiere renunciar a dos pares de esquís en la Planta 1.

Ventaja comparativa y curva de posibilidades de producción

Para construir una curva de posibilidades de producción combinada para las tres plantas, podemos comenzar preguntando cuántos pares de esquís Alpine Sports podrían producir si solo produjeran esquís. Para encontrar esta cantidad, sumamos los valores en las intercepciones verticales de cada una de las curvas de posibilidades de producción en [Figura 3 - Posibilidades de Producción en Tres Plantas]. Estas intercepciones nos indican el número máximo de pares de esquís que puede producir cada planta. La planta 1 puede producir 200 pares de esquís al mes, la Planta 2 puede producir 100 pares de esquís al mes y la Planta 3 puede producir 50 pares. Alpine Sports puede así producir 350 pares de esquís al mes si dedica sus recursos exclusivamente a la producción de esquí. En ese caso, no produce tablas de snowboard.

Ahora supongamos que la firma decide producir 100 tablas de snowboard. Eso requerirá desplazar una de sus plantas fuera de la producción de esquí. ¿Cuál elegirá cambiar? Lo sensato que debe hacer es elegir la planta en la que las tablas de snowboard tengan el menor costo de oportunidad —Planta 3. Tiene una ventaja no porque pueda producir más tablas de snowboard que las otras plantas (todas las plantas en este ejemplo son capaces de producir hasta 100 tablas de snowboard al mes) sino porque es la planta menos productiva para hacer esquís. Producir una tabla de snowboard en la Planta 3 requiere renunciar a solo medio par de esquís.

Los economistas dicen que una economía tiene una ventaja comparativa en la producción de un bien o servicio si el costo de oportunidad de producir ese bien o servicio es menor para esa economía que para cualquier otra. La planta 3 tiene una ventaja comparativa en la producción de snowboard debido a que es la planta para la que el costo de oportunidad de tablas de snowboard adicionales es menor. Para poner esto en términos de la curva de posibilidades de producción, la Planta 3 tiene una ventaja comparativa en la producción de snowboard (la buena en el eje horizontal) porque su curva de posibilidades de producción es la más plana de las tres curvas.

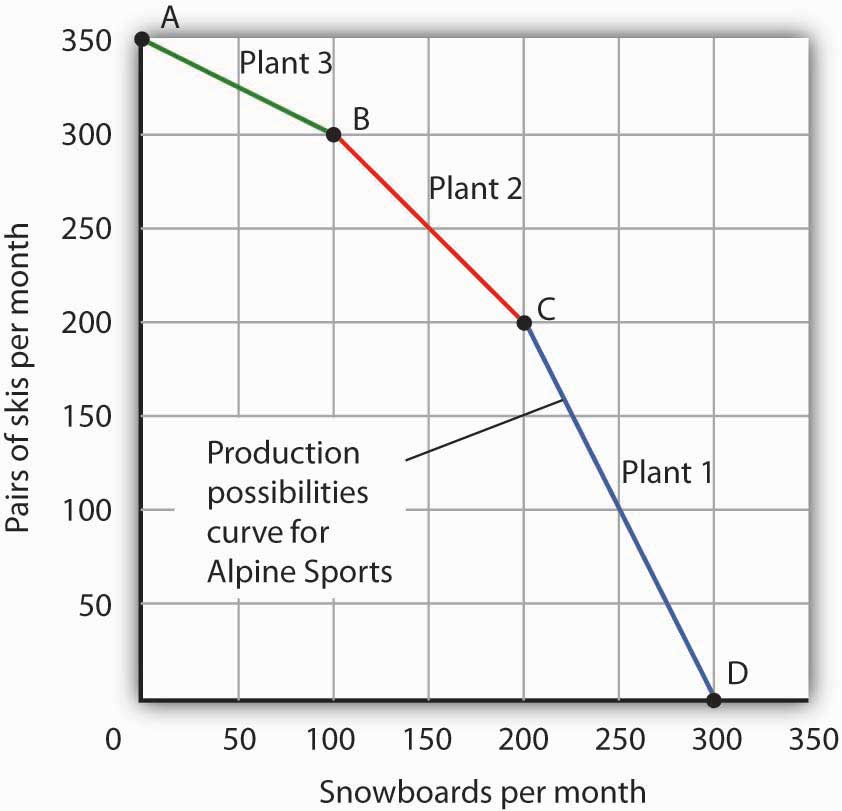[Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos]

La curva mostrada combina las curvas de posibilidades de producción para cada planta. En el punto A, Alpine Sports produce 350 pares de esquís al mes y sin tablas de snowboard. Si la firma desea incrementar la producción de snowboard, primero utilizará la Planta 3, que tiene una ventaja comparativa en tablas de snowboard.

La ventaja comparativa de la planta 3 en la producción de snowboard hace un punto crucial sobre la naturaleza de la ventaja comparativa. No tiene por qué implicar que una planta en particular sea especialmente buena en una actividad. En nuestro ejemplo, las tres plantas son igualmente buenas en la producción de snowboard. La planta 3, sin embargo, es la menos eficiente de las tres en la producción de esquí. Alpine cede así menos esquís cuando produce tablas de snowboard en la Planta 3. Por lo tanto, la ventaja comparativa puede provenir de una falta de eficiencia en la producción de un bien alternativo y no de una competencia especial en la producción del primer bien.

La curva de posibilidades de producción combinada para las tres plantas de la firma se muestra en [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos]. Comenzamos en el punto A, con las tres plantas produciendo solo esquís. La producción totaliza 350 pares de esquís por mes y cero tablas de snowboard. Si la firma produjera 100 tablas de snowboard en la Planta 3, la producción de esquí caería 50 pares al mes (recordemos que el costo de oportunidad por tabla de snowboard en la Planta 3 es de medio par de esquís). Eso llevaría la producción de esquí a 300 parejas, en el punto B. Si Alpine Sports produjera aún más tablas de snowboard en un solo mes, cambiaría la producción a la Planta 2, la instalación con el siguiente costo de oportunidad más bajo. Producir 100 tablas de snowboard en la Planta 2 dejaría a Alpine Sports produciendo 200 tablas de snowboard y 200 pares de esquís al mes, en el punto C. Si la firma cambiara por completo a la producción de snowboard, la Planta 1 sería la última en cambiar porque el costo de cada snowboard hay 2 pares de esquís. Con las tres plantas produciendo solo tablas de snowboard, la firma se encuentra en el punto D en la curva de posibilidades de producción combinada, produciendo 300 tablas de snowboard al mes y sin esquís.

Observe que esta curva de posibilidades de producción, que se compone de segmentos lineales de cada planta de ensamblaje, tiene una forma abowed-out; el valor absoluto de su pendiente aumenta a medida que Alpine Sports produce cada vez más tablas de snowboard. Esto es resultado de transferir recursos de la producción de un bien a otro según la ventaja comparativa. Examinaremos la importancia de la forma abovedada de la curva en la siguiente sección.

La Ley de Incrementar el Costo de Oportunidad

Vemos en [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos] que, comenzando en el punto A y produciendo solo esquís, los deportes alpinos experimentan costos de oportunidad cada vez más altos ya que produce más tablas de snowboard. El hecho de que el costo de oportunidad de las tablas de snowboard adicionales aumente a medida que la firma produce más de ellas es un reflejo de una importante ley económica. La ley de aumentar el costo de oportunidad sostiene que a medida que una economía se mueve a lo largo de su curva de posibilidades de producción en la dirección de producir más de un bien particular, el costo de oportunidad de unidades adicionales de ese bien aumentará.

Hemos visto la ley de aumentar el costo de oportunidad en el trabajo viajando desde el punto A hacia el punto D en la curva de posibilidades de producción en [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos]. El costo de oportunidad de cada una de las primeras 100 tablas de snowboard equivale a medio par de esquís; cada una de las siguientes 100 tablas de snowboard tiene un costo de oportunidad de 1 par de esquís, y cada una de las últimas 100 tablas de snowboard tiene un costo de oportunidad de 2 pares de esquís. La ley también se aplica ya que la firma cambia de tablas de snowboard a esquís. Supongamos que comienza en el punto D, produciendo 300 tablas de snowboard al mes y sin esquís. Puede cambiar a la producción de esquí a un costo relativamente bajo al principio. El costo de oportunidad de los primeros 200 pares de esquís es de solo 100 tablas de snowboard en la Planta 1, un movimiento del punto D al punto C, o 0.5 tablas de snowboard por par de esquís. Diríamos que la Planta 1 tiene una ventaja comparativa en la producción de esquí. Los siguientes 100 pares de esquís se producirían en la Planta 2, donde la producción de snowboard caería 100 tablas al mes. El costo de oportunidad de los esquís en la Planta 2 es de 1 snowboard por par de esquís. La planta 3 sería la última planta convertida a producción de esquí. Allí, se podrían producir 50 pares de esquís por mes a un costo de 100 tablas de snowboard, o un costo de oportunidad de 2 tablas de snowboard por par de esquís.

La curva de posibilidades de producción reducida para los deportes alpinos ilustra la ley de aumentar el costo de oportunidad. La escasez implica que una curva de posibilidades de producción es descendente; la ley de aumentar el costo de oportunidad implica que se inclinará, o cóncava, en forma.

La curva abolida de [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos] se vuelve más suave a medida que incluimos más instalaciones de producción. Supongamos que Alpine Sports se expande a 10 plantas, cada una con una curva de posibilidades de producción lineal El panel (a) de [Figura 5 - Posibilidades de producción para la economía] muestra la curva combinada para la firma expandida, construida como lo hicimos en [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos]. Esta curva de posibilidades de producción incluye 10 segmentos lineales y es casi una curva suave. A medida que incluimos cada vez más unidades de producción, la curva se volverá más suave y más suave. En una economía real, con un tremendo número de empresas y trabajadores, es fácil ver que la curva de posibilidades de producción será suave. Generalmente dibujaremos curvas de posibilidades de producción para la economía como curvas suaves y curvadas, como la del Panel (b). Esta curva de posibilidades de producción muestra una economía que produce únicamente esquís y tablas de snowboard. Observe que la curva todavía tiene una forma abowed-out; todavía tiene una pendiente negativa. Observe también que esta curva no tiene números. Los economistas suelen utilizar modelos como el modelo de posibilidades de producción con gráficas que muestran las formas generales de las curvas pero que no incluyen números específicos.

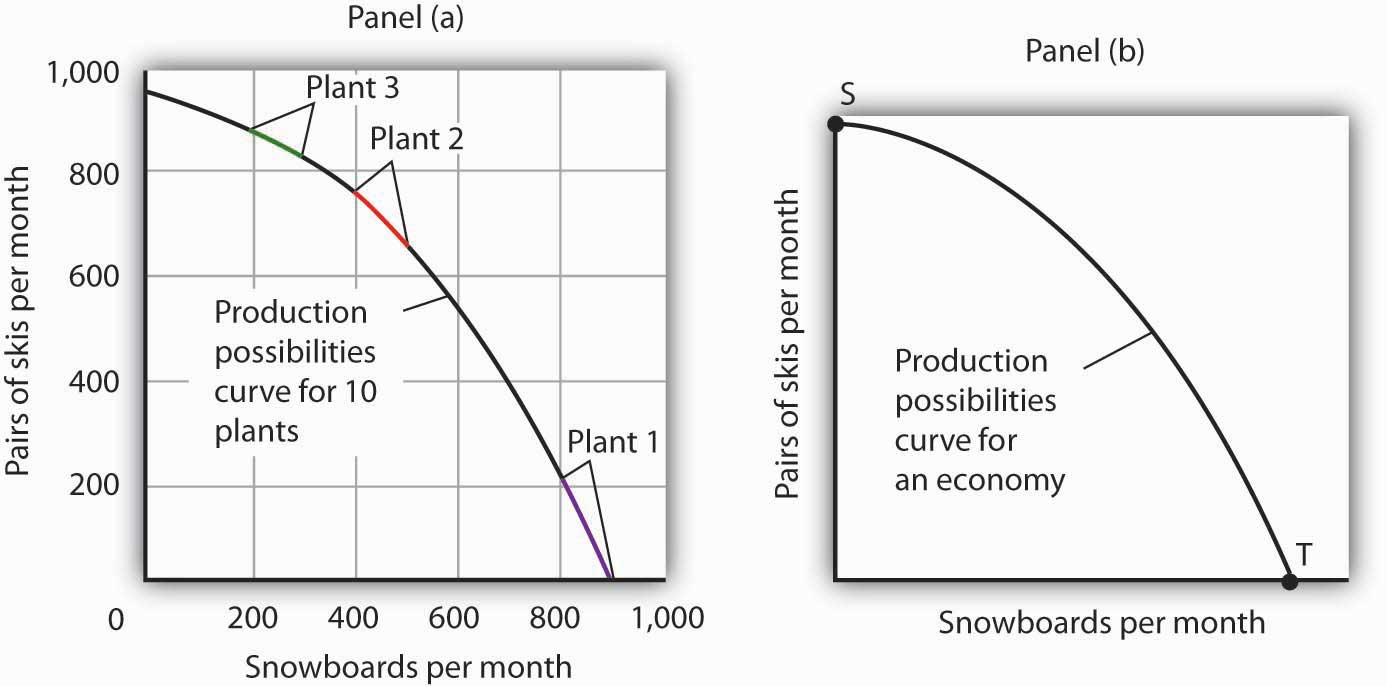
[Figura 5 - Posibilidades de producción para la economía]

A medida que combinamos las curvas de posibilidades de producción para cada vez más unidades, la curva se vuelve más suave. Conserva su pendiente negativa y su forma abochada. En el Panel (a) tenemos una curva combinada de posibilidades de producción para Alpine Sports, asumiendo que ahora cuenta con 10 plantas productoras de esquís y tablas de snowboard. A pesar de que cada una de las plantas tiene una curva lineal, combinándolas de acuerdo con la ventaja comparativa, como hicimos con 3 plantas en [Figura 4 - La curva de posibilidades de producción combinada para deportes alpinos], produce lo que parece ser una curva suave, no lineal, a pesar de que está conformada por lineal segmentos. Al trazar las curvas de posibilidades de producción para la economía, generalmente asumiremos que son suaves y “inclinadas”, como en el Panel (b). Esta curva representa toda una economía que produce solo esquís y tablas de snowboard.

Video: Posibilidades de Producción

Para otra forma de ver la curva de posibilidades de producción, vea el siguiente video del profesor de economía Jacob Clifford. Utilizó la película Monsters, Inc. para explicar la curva de posibilidades de producción de una manera más fácil de entender.

Responda las preguntas de autoverificación a continuación para monitorear su comprensión de los conceptos en esta sección.

Preguntas de Self Check

1. ¿Cómo construirías una curva de posibilidades de producción?
2. ¿Cuál es la ventaja comparativa en la economía?
3. Describir la ley del costo de oportunidad.
4. Nombra tres puntos hechos en el video por Jacob Clifford.