1.3: Definición de segmentos de línea
- Page ID
- 107641
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar la longitud Positiva entre puntos.
Medición de la distancia entre dos puntos
La distancia es la medida de longitud entre dos puntos. Medir es determinar qué tan separados están dos objetos geométricos. La forma más común de medir la distancia es con una regla. Las reglas de pulgada generalmente se dividen por segmentos de octava pulgada (o 0.125 pulgadas). Las reglas de centímetros se dividen por segmentos de décimo centímetro (o 0.1 cm). Tenga en cuenta que la distancia entre dos puntos es el valor absoluto de la diferencia entre los números mostrados en la regla. Esto implica que no es necesario comenzar a medir en “0”, siempre y cuando restes el primer número del segundo.
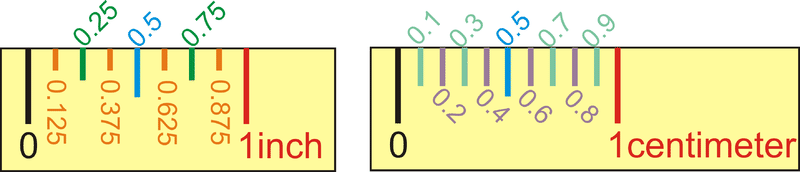Figura\(\PageIndex{1}\)El postulado de adición de segmento establece que si\(A\)\(B\),, y\(C\) son colineales y\(B\) es entre\(A\) y\(C\), entonces\(AB+BC=AC\).
Figura\(\PageIndex{2}\)Puedes encontrar las distancias entre puntos en el\(x–y\) plano si las líneas son horizontales o verticales. Si la línea es vertical, busque el cambio en las\(y\) coordenadas −. Si la línea es horizontal, busque el cambio en las\(x\) coordenadas −.
Supongamos que quieres medir tu altura, pero la cinta métrica que tienes es vieja y el extremo está roto. Si la cinta ahora comienza a los 6 cm y lee 138 cm desde el suelo hasta la parte superior de tu cabeza, ¿qué altura tienes?
Ejemplo\(\PageIndex{1}\)
¿Cuál es la distancia marcada en la regla de abajo? El gobernante está en centímetros.
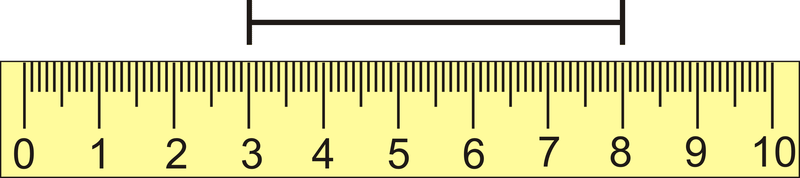Figura\(\PageIndex{3}\)Solución
Restar un punto final del otro. El segmento de línea abarca de 3 cm a 8 cm.
\(|8−3|=|5|=5\)
El segmento de línea es de 5 cm de largo. Observe que también podría haber hecho
\(|3−8|=|−5|=5\).
Ejemplo\(\PageIndex{2}\)
Hacer un boceto de\(\overline{OP}\), donde\(Q\) esta entre\(O\) y\(P\).
Solución
Dibuja\(\overline{OP}\) primero, luego coloca\(Q\) en el segmento.
Figura\(\PageIndex{4}\)Ejemplo\(\PageIndex{3}\)
¿Cuál es la distancia entre los dos puntos que se muestran a continuación?
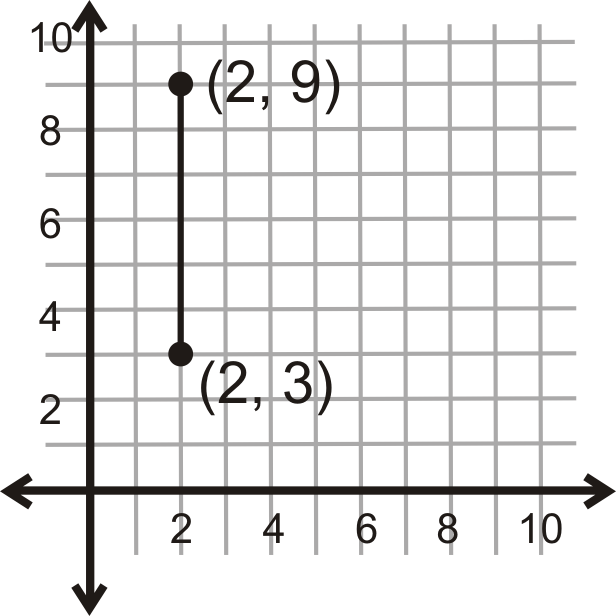Figura\(\PageIndex{5}\)Solución
Debido a que esta línea es vertical, mira el cambio en las\(y\) coordenadas.
\(|9−3|=|6|=6\)
La distancia entre los dos puntos es de 6 unidades.
Ejemplo\(\PageIndex{4}\)
En la imagen del Ejemplo 2, si\(OP=17\) y\(QP=6\), ¿qué es\(OQ\)?
Solución
\(OQ+QP=OP\)
\(OQ+6=17\)
\(OQ=17−6\)
\(OQ=11\)
Ejemplo\(\PageIndex{5}\)
¿Cuál es la distancia entre los dos puntos que se muestran a continuación?
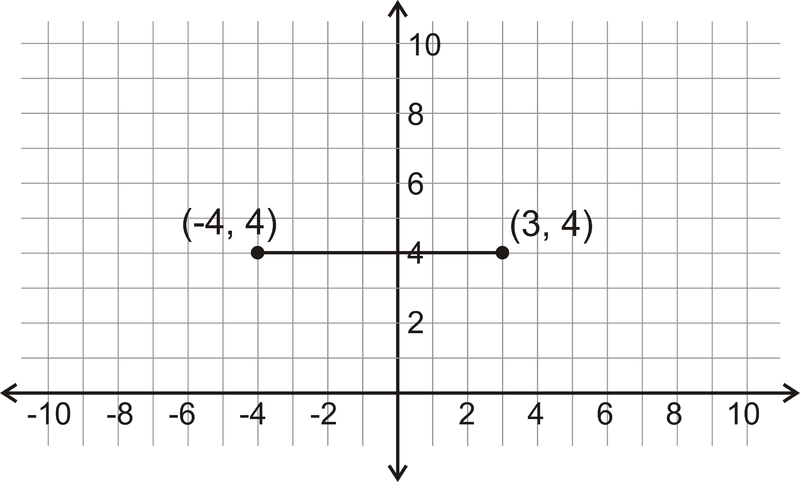Figura\(\PageIndex{6}\)Solución
Debido a que esta línea es horizontal, mire el cambio en las\(x\) coordenadas.
\(|(−4)−3|=|−7|=7\)
La distancia entre los dos puntos es de 7 unidades.
Revisar
Para 1-4, use la regla en cada imagen para determinar la longitud del segmento de línea.
-
Figura\(\PageIndex{7}\) -
Figura\(\PageIndex{8}\) -
Figura\(\PageIndex{9}\) -
Figura\(\PageIndex{10}\) - Hacer un boceto de\(\overline{BT}\), con\(A\) entre\(B\) y\(T\).
- Si O está en medio de\(\overline{LT}\), ¿dónde se encuentra exactamente? Si\(LT=16 cm\), ¿qué es\(LO\) y\(OT\)?
- Para tres puntos colineales,\(A\) entre\(T\) y\(Q\):
- Dibuja un boceto.
- Escribe el Postulado de Adición de Segmentos para tu boceto.
- Si\(AT=10\) dentro y\(AQ=5\) dentro, ¿qué es\(TQ\)?
- Para tres puntos colineales,\(M\) entre\(H\) y\(A\):
- Dibuja un boceto.
- Escribe el Postulado de Adición de Segmentos para tu boceto.
- Si\(HM=18 cm\) y\(HA=29 cm\), ¿qué es\(AM\)?
- Para tres puntos colineales, I entre M y T:
- Dibuja un boceto.
- Escribe el Postulado de Adición de Segmentos para tu boceto.
- Si\(IT=6 cm\) y\(MT=25 cm\), ¿qué es\(AM\)?
- Haz un boceto que coincida con la descripción: B está entre\(A\) y\(D\). \(C\)está entre\(B\) y\(D\). \(AB=7 cm\),\(AC=15 cm\), y\(AD=32 cm\). Encontrar\(BC\),\(BD\), y\(CD\).
- Hacer un boceto que coincida con la descripción:\(E is between \(F\) y\(G\). \(H\)está entre\(F\) y\(E\). \(FH=4 in\),\(EG=9 in\), y\(FH=HE\). Encontrar\(FE\),\(HG\), y\(FG\).
Para 12 y 13, Supongamos que\(J\) está entre\(H\) y\(K\). Utilice el Postulado de Adición de Segmentos para resolver\(x\). Después encuentra la longitud de cada segmento.
- \(HJ=4x+9\),\(JK=3x+3\),\(KH=33\)
- \(HJ=5x−3\),\(JK=8x−9\),\(KH=131\)
Para 14-17, determinar la distancia vertical u horizontal entre los dos puntos.
-
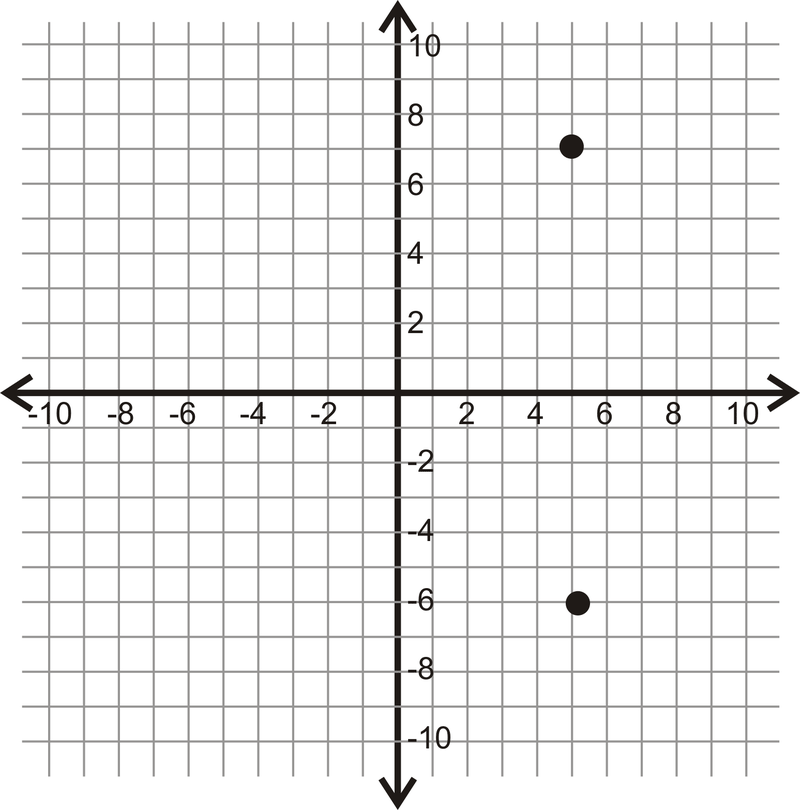Figura\(\PageIndex{11}\) -
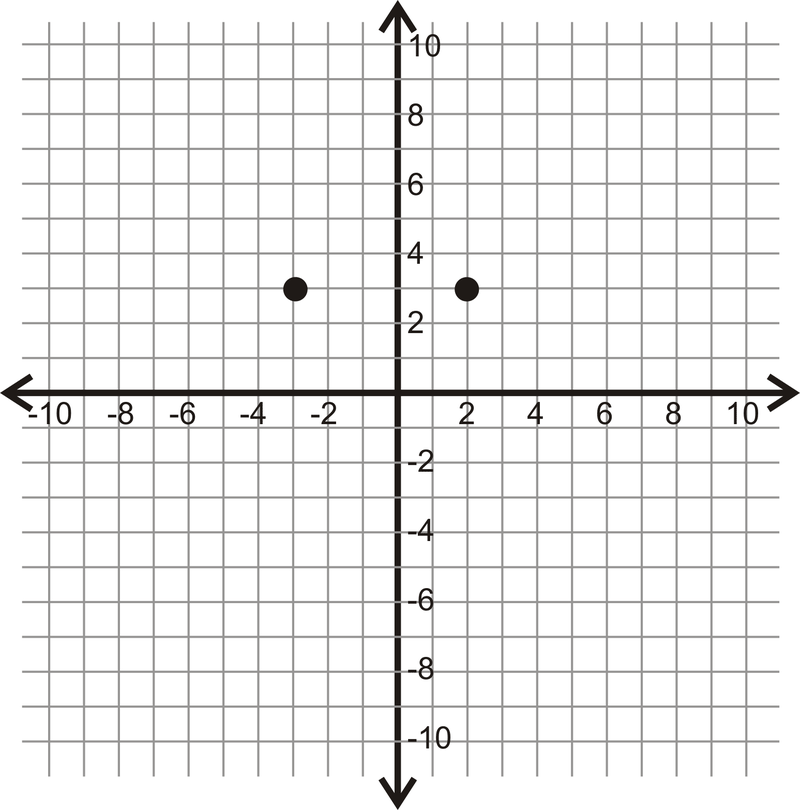Figura\(\PageIndex{12}\) -
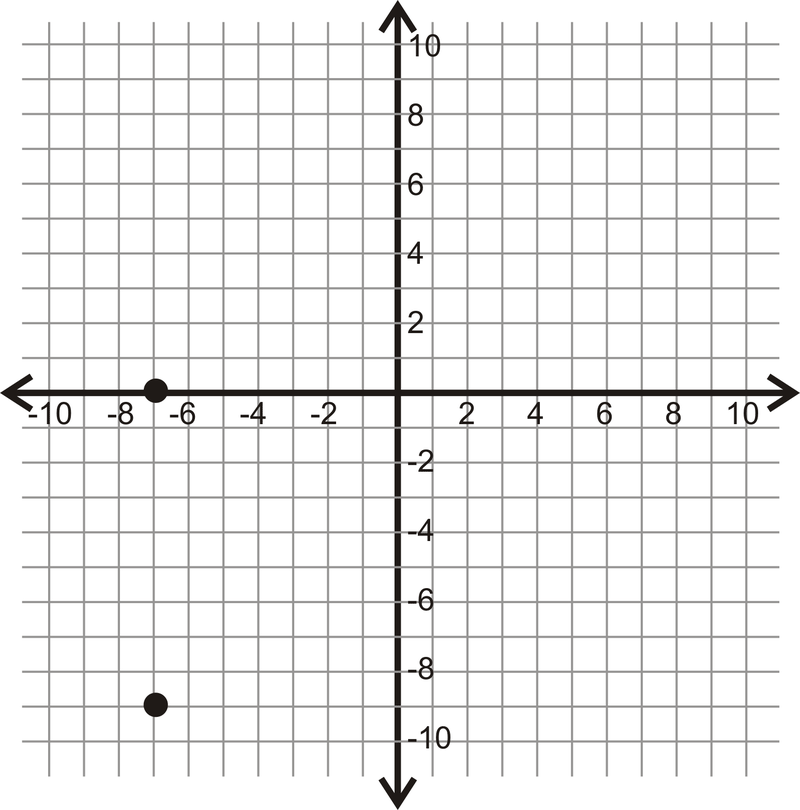Figura\(\PageIndex{13}\) -
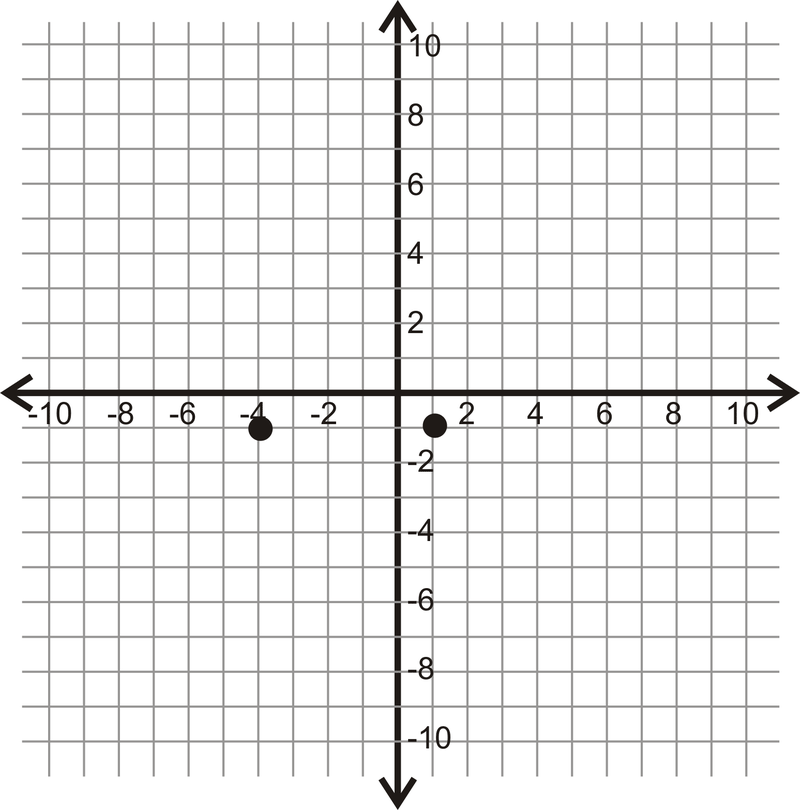Figura F\(\PageIndex{14}\) - Hacer un boceto de:\(S\) está entre\(T\) y\(V\). \(R\)está entre\(S\) y\(T\). \(TR=6\),\(RV=23\), y\(TR=SV\).
- Encuentra\(SV\),\(TS\),\(RS\) y\(TV\) de #18.
- Porque\(\overline{HK}\), supongamos que\(J\) es entre\(H\) y\(K\). Si\(HJ=2x+4\),\(JK=3x+3\), y\(KH=22\), encuentra\(x\).
El vocabulario
| Término | Definición |
|---|---|
| distancia | La distancia es la medida de longitud entre dos puntos. |
| Valor Absoluto | El valor absoluto de un número es la distancia que el número es de cero. Los valores absolutos nunca son negativos. |
| medir | Medir la distancia es determinar qué tan separados están dos objetos geométricos mediante el uso de una línea numérica o regla. |
Recursos adicionales
Elemento Interactivo
Video: Postulado de Regla y Postulado de Adición de Segmentos
Actividades: Distancia entre dos puntos Preguntas de discusión
Ayudas de estudio: Guía de estudio de segmentos
Práctica: Definición de Segmento de Línea
Mundo Real: Distancia Entre Dos Puntos