1.18: Clasificar Polígonos
- Page ID
- 107598
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Categorías de polígonos basados en el número de lados, y si son cóncavos o convexos.
Polígonos
Un polígono es cualquier figura bidimensional cerrada que está hecha completamente de segmentos de línea que se cruzan en sus puntos finales. Los polígonos pueden tener cualquier número de lados y ángulos, pero los lados nunca pueden ser curvados. Los segmentos se denominan lados de los polígonos, y los puntos donde se cruzan los segmentos se denominan vértices.
Los polígonos pueden ser convexos o cóncavos. El término cóncavo se refiere a una cueva, o el polígono es “espeleología”. Todas las estrellas son polígonos cóncavos.
Figura\(\PageIndex{1}\)Un polígono convexo no se hunde. Los polígonos convexos se ven así:
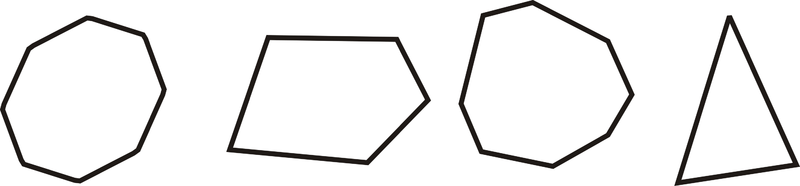Figura\(\PageIndex{2}\)Una diagonal es un segmento de línea no lateral que conecta dos vértices de un polígono convexo.
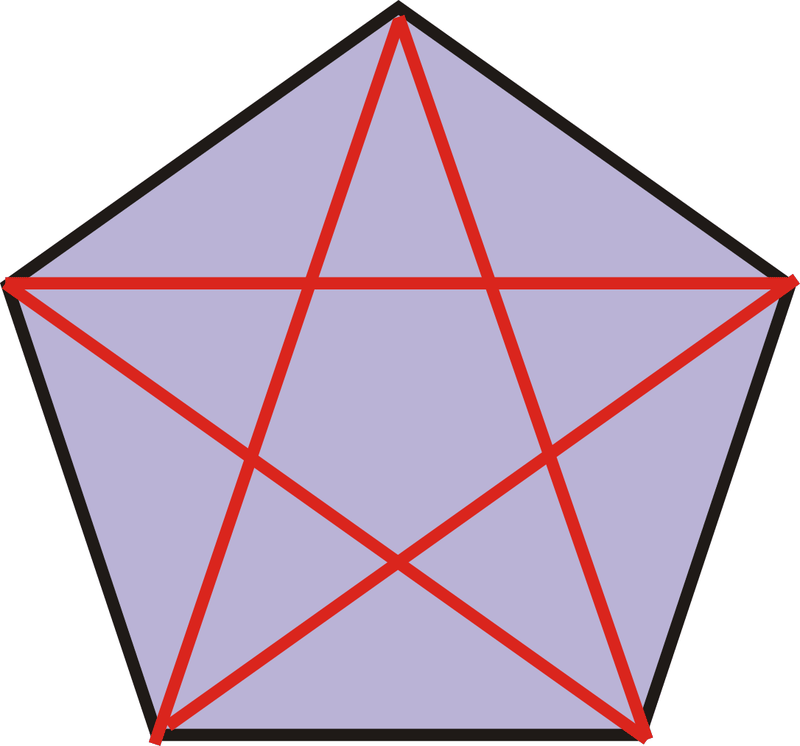Figura\(\PageIndex{3}\)Los segmentos de línea roja son todos diagonales. Este pentágono tiene 5 diagonales.
Ya sea que un polígono sea convexo o cóncavo, siempre se le nombra por el número de lados. Explora la relación entre el número de lados de un polígono convexo y sus diagonales. ¿Puedes completar la mesa?
| Nombre del polígono | Número de lados | Número de diagonales | Ejemplo convexo |
|---|---|---|---|
| Triángulo | 3 | 0 |
 Figura\(\PageIndex{4}\) |
| Cuadrilátero | 4 | 2 |
 Figura\(\PageIndex{5}\) |
| Pentágono | 5 | 5 |
 Figura\(\PageIndex{6}\) |
| Hexágono | 6 | 9 |
 Figura\(\PageIndex{7}\) |
| Heptágono | 7 | ? |
 Figura\(\PageIndex{8}\) |
| Octágono | 8 | ? |
 Figura\(\PageIndex{9}\) |
| Nonagon | 9 | ? |
 Figura\(\PageIndex{10}\) |
| Decagon | 10 | ? |
 Figura\(\PageIndex{11}\) |
| Undecagon o hendecagon | 11 | ? |
 Figura\(\PageIndex{12}\) |
| Dodecagon | 12 | ? |
 Figura\(\PageIndex{13}\) |
| n-gon | n (donde n>12) | ? |
 Figura\(\PageIndex{14}\) |
¿Y si te dijeran cuántos lados tiene un polígono? ¿Cómo describirías el polígono a partir de esa información?
Ejemplo\(\PageIndex{1}\)
¿Cuál de las siguientes figuras es un polígono?
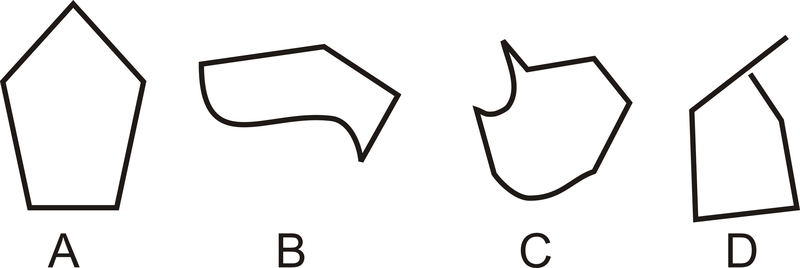Figura\(\PageIndex{15}\)Solución
La forma más fácil de identificar el polígono es identificar qué formas no son polígonos. B y C tienen cada uno al menos un lado curvo, por lo que no son polígonos. D tiene todos los lados rectos, pero uno de los vértices no está en el punto final, por lo que no es un polígono. A es el único polígono.
Ejemplo\(\PageIndex{2}\)
Determina si las siguientes formas son convexas o cóncavas.
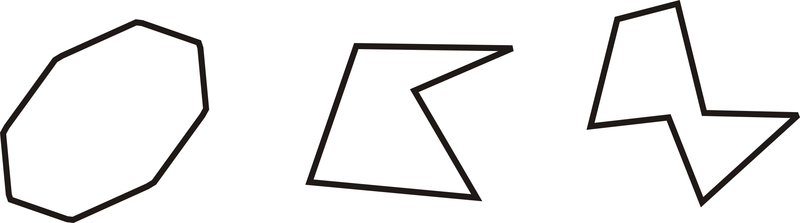Figura\(\PageIndex{16}\)Solución
Para ver si un polígono es cóncavo, mire los polígonos y vea si algún ángulo “se hunde” al interior del polígono. El primer polígono no hace esto, por lo que es convexo. Los otros dos lo hacen, por lo que son cóncavos.
Ejemplo\(\PageIndex{3}\)
Nombra los tres polígonos de abajo por su número de lados y si es convexo o cóncavo.
Figura\(\PageIndex{17}\)Solución
El polígono rosa es un hexágono cóncavo (6 lados).
El polígono verde pentágono convexo (5 lados).
El polígono amarillo es un decágono convexo (10 lados).
Ejemplo\(\PageIndex{4}\)
Dibuja un polígono de 7 lados, también llamado heptágono. ¿Cuántas diagonales tiene un heptágono?
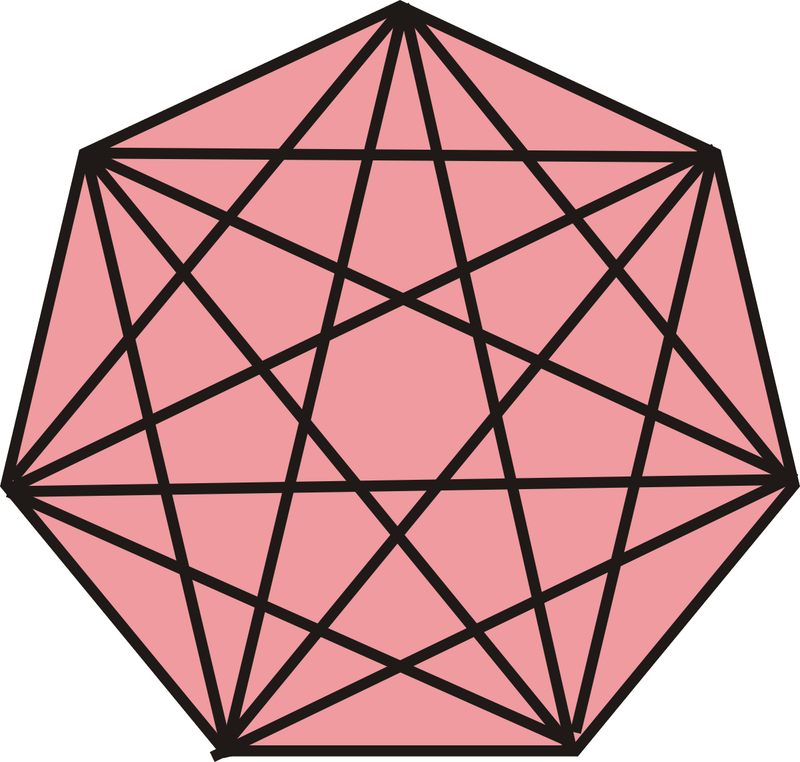Figura\(\PageIndex{18}\)Solución
Primero, dibuja el heptágono. Dibujando en todas las diagonales y contándolas, vemos que hay 14.
Ejemplo\(\PageIndex{5}\)
Verdadero o falso: Un cuadrilátero es siempre un cuadrado.
Solución
Falso. Sólo los cuadriláteros con cuatro lados congruentes y cuatro ángulos rectos serán cuadrados. Hay muchos cuadriláteros (como rectángulos, cometas, paralelogramos, trapezoides, etc.) que no son necesariamente cuadrados.
Revisar
En los problemas 1-6, nombra cada polígono con el mayor detalle posible.
-
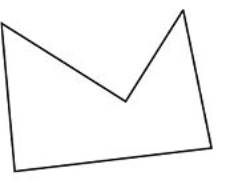Figura\(\PageIndex{19}\) -
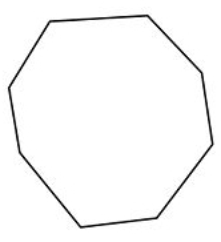Figura\(\PageIndex{20}\) -
Figura\(\PageIndex{21}\) -
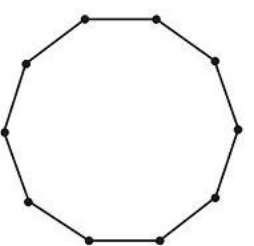Figura\(\PageIndex{22}\) -
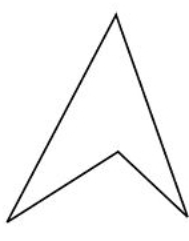Figura\(\PageIndex{23}\) -
Figura\(\PageIndex{24}\) - Explique por qué las siguientes figuras NO son polígonos:
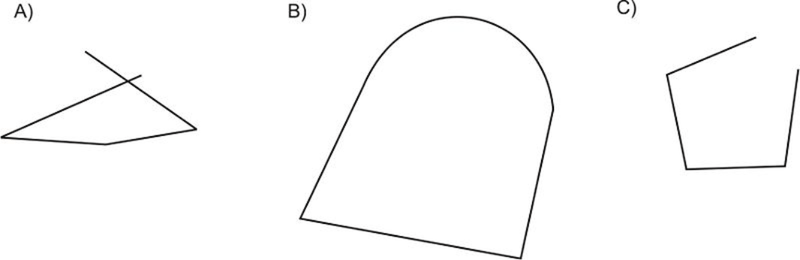Figura\(\PageIndex{25}\) - ¿Cuántas diagonales puedes dibujar de un vértice de un pentágono? Dibuja un boceto de tu respuesta.
- ¿Cuántas diagonales puedes dibujar de un vértice de un octágono? Dibuja un boceto de tu respuesta.
- ¿Cuántas diagonales puedes dibujar de un vértice de un dodecágono?
- Determinar el número de diagonales totales para un octágono, nonagon, decágono, undecagon y dodecagon.
Para 12-14, determinar si la declaración es verdadera o falsa.
- Un polígono debe estar encerrado.
- Una estrella es un polígono convexo.
- Una estrella de 5 puntos es un decagón.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.12.
Recurso
El vocabulario
| Término | Definición |
|---|---|
| diagonal (de un polígono) | Un segmento de línea no lateral que conecta dos vértices de un polígono convexo. |
| Polígono | Un polígono es una simple figura cerrada con al menos tres lados rectos. |
| Cóncava | Un polígono cóncavo tiene al menos un ángulo interior mayor a 180 grados. Una forma común de identificar un polígono cóncavo es buscar un lado “hundido” del polígono. |
| Convexo | Un polígono convexo no contiene ángulos interiores mayores de 180 grados. |
| Diagonal | Una diagonal es un segmento de línea en un polígono que conecta vértices no consecutivos |
| Ángulos exteriores | Un ángulo exterior es el ángulo formado por un lado de un polígono y la extensión del lado adyacente. |
| Ángulos interiores | Los ángulos interiores son los ángulos dentro de una figura. |
| Polígono Regular | Un polígono regular es un polígono con todos los lados de la misma longitud y todos los ángulos la misma medida. |
| Vértices | Los vértices son puntos donde los segmentos de línea se cruzan. |
| Equilátero | Un polígono es equilátero si todos sus lados tienen la misma longitud. |
Recurso Adicional
Elemento interactivo
Video: Suma de ángulos interiores de un polígono
Actividades: Clasificación de polígonos Preguntas de discusión
Ayudas de estudio: Guía de estudio de polígonos
Práctica: Clasificar polígonos
Mundo real: Polígonos de la naturaleza