1.17: Ángulos Verticales
- Page ID
- 107640
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Entender que los ángulos verticales son opuestos entre sí y tienen la misma medida.
Los ángulos verticales son dos ángulos no adyacentes formados por líneas que se cruzan. \(\angle 1\)y\(\angle 3\) son ángulos verticales y\(\angle 2\) y\(\angle 4\) son ángulos verticales.
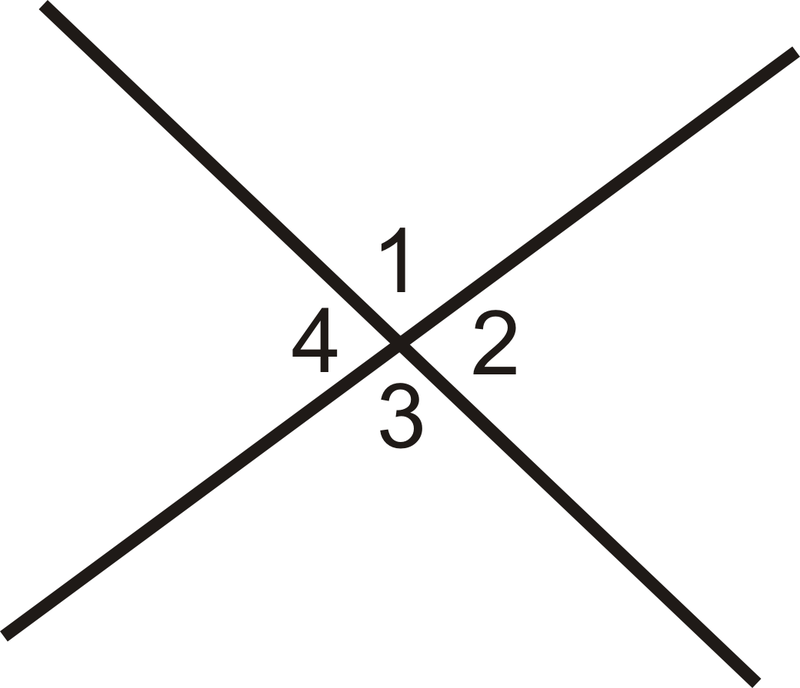Figura\(\PageIndex{1}\)El Teorema de Ángulos Verticales establece que si dos ángulos son ángulos verticales, entonces son congruentes.
¿Y si te dieran dos ángulos de tamaño desconocido y te dijeran que son ángulos verticales? ¿Cómo determinarías sus medidas de ángulo?
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de\(x\).
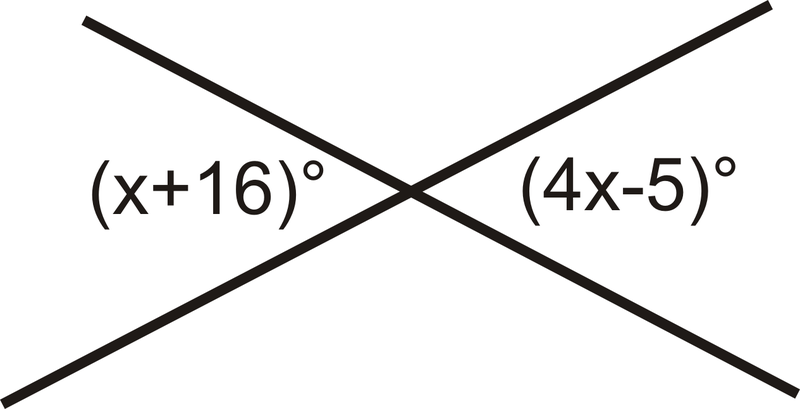Figura\(\PageIndex{2}\)Solución
Los ángulos verticales son congruentes, así que establece los ángulos iguales entre sí y resuelve para\(x\).
\(x+16=4x−5\)
\(3x=21\)
\(x=7^{\circ}\)
Ejemplo\(\PageIndex{2}\)
Encuentra el valor de\(y\).
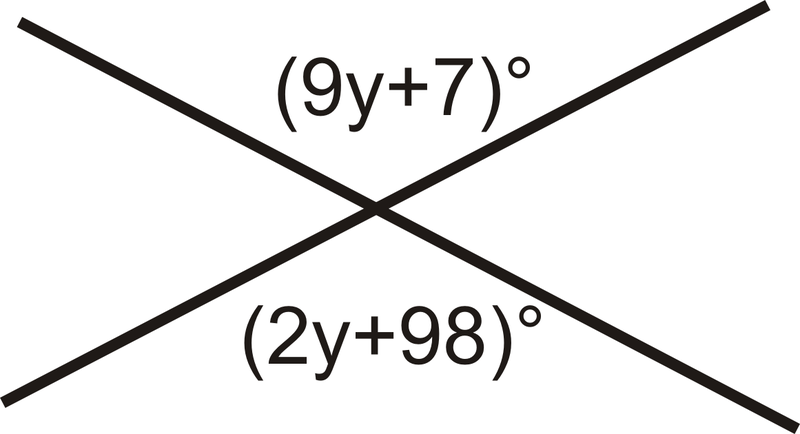Figura\(\PageIndex{3}\)Solución
Los ángulos verticales son congruentes, así que establece los ángulos iguales entre sí y resuelve para\(y\).
\(9y+7=2y+98\)
\(7y=91\)
\(y=13^{\circ}\)
Ejemplo\(\PageIndex{3}\)
Encuentra\(m\angle 1\).
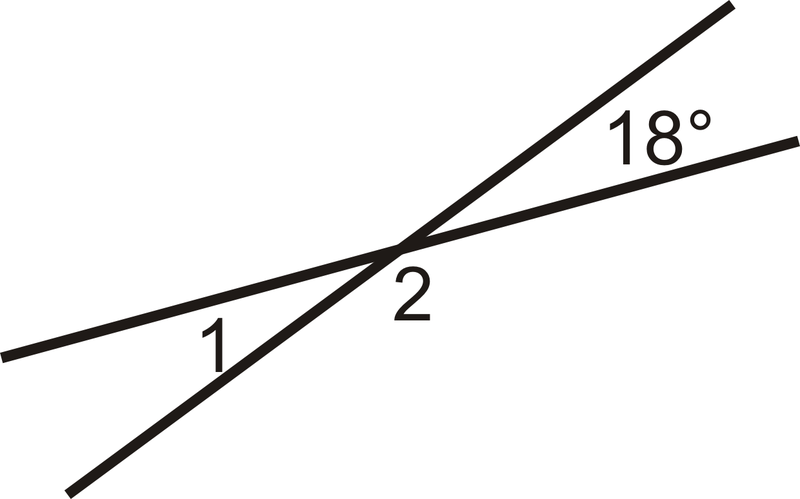Figura\(\PageIndex{4}\)Solución
\(\angle 1\)es ángulos verticales con\(18^{\circ}\), entonces\ (m\ ángulo 1=18^ {\ circ}.
Ejemplo\(\PageIndex{4}\)
Si\ ángulo ABC y\ ángulo DEF son ángulos verticales y\ (m\ ángulo ABC= (4x+10) ^ {\ circ} y\ (m\ ángulo DEF= (5x+2) ^ {\ circ}, ¿cuál es la medida de cada ángulo?
Solución
Los ángulos verticales son congruentes, así que establece los ángulos iguales entre sí y resuelve para x Luego regresa para encontrar la medida de cada ángulo.
\(4x+10=5x+2\)
\(x=8\)
Entonces,\(m\angle ABC=m\angle DEF=(4(8)+10)^{\circ}=42^{\circ}\)
Ejemplo\(\PageIndex{5}\)
Verdadero o falso: los ángulos verticales son siempre menores de 90^ {\ circ}.
Solución
Esto es falso, puedes tener ángulos verticales que son más de 90^ {\ circ}. Los ángulos verticales son menores de 180^ {\ circ}.
Revisar
Usa el diagrama a continuación para los ejercicios 1-2. Tenga en cuenta que\(\overline{NK} \perp \overleftrightarrow{IL}\).
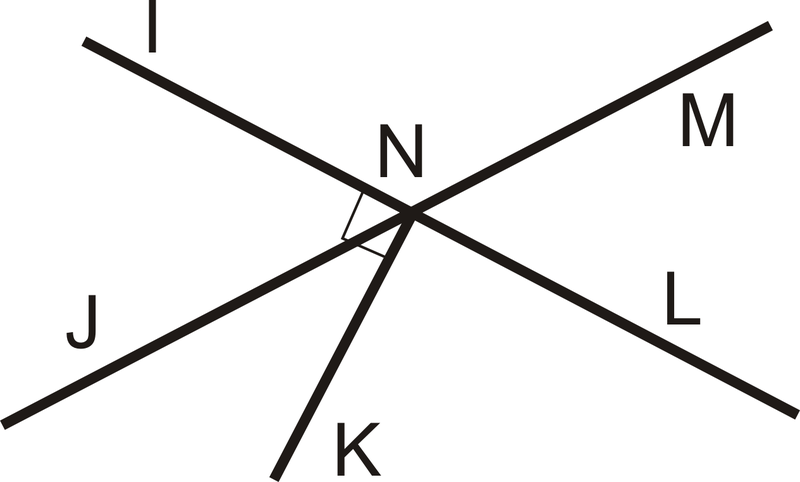Figura\(\PageIndex{5}\)- Nombra un par de ángulos verticales.
- Si\(m\angle INJ=63^{\circ}\), encuentra\(m\angle MNL\).
Para el ejercicio 3, determinar si la declaración es verdadera o falsa.
- Los ángulos verticales tienen el mismo vértice.
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(9x+1)^{\circ}\) y\(m\angle DEF=(5x+29)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(8x+2)^{\circ}\) y\(m\angle DEF=(2x+32)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(x+22)^{\circ}\) y\(m\angle DEF=(5x+2)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(3x+12)^{\circ}\) y\(m\angle DEF=(7x)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(5x+2)^{\circ}\) y\(m\angle DEF=(x+26)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(3x+1)^{\circ}\) y\(m\angle DEF=(2x+2)^{\circ}\), ¿cuál es la medida de cada ángulo?
- Si\(\angle ABC\) y\(\angle DEF\) son ángulos verticales y\(m\angle ABC=(6x−3)^{\circ}\) y\(m\angle DEF=(5x+1)^{\circ}\), ¿cuál es la medida de cada ángulo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.10.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulos Verticales | Los ángulos verticales son un par de ángulos opuestos creados por líneas que se cruzan. |
| Teorema de ángulos verticales | El Teorema de Ángulos Verticales establece que si dos ángulos son verticales, entonces son congruentes. |
Recursos adicionales
Elemento Interactivo
Video: Ángulos complementarios, suplementarios y verticales
Actividades: Preguntas de discusión sobre ángulos verticales
Ayudas de estudio: Guía de estudio de ángulos
Práctica: Ángulos verticales
Mundo Real: Ángulos Verticales