2.10: Declaraciones negativas
- Page ID
- 107351
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Valores de verdad para la negación de declaraciones condicionales, conjunciones y disyunciones.
En el discurso cotidiano, las declaraciones negativas suelen ser ambiguas o poco claras. Matemáticamente, se necesita una manera precisa de negar declaraciones para que pueda determinar con precisión si las declaraciones son verdaderas o falsas. ¿Cuándo es cierta la negación de la siguiente frase?
Si no tengo frío entonces no está nevando.
Negaciones
Mientras que en el lenguaje cotidiano lo contrario de “perro” podría ser “gato”, en matemáticas lo contrario de “perro” es “no un perro”. Usar la palabra “no” es la forma básica de negar una oración atómica. Una oración atómica es una declaración lógica sin conectivos lógicos que tiene un valor de verdad.
- Sentencia original\((D)\): Esa cosa es un perro.
- Negación de frase\((\sim D)\): Esa cosa no es un perro.
El cuadro de abajo representa el universo de todas las cosas. Este universo se puede separar en cosas que son perros y cosas que no son perros.
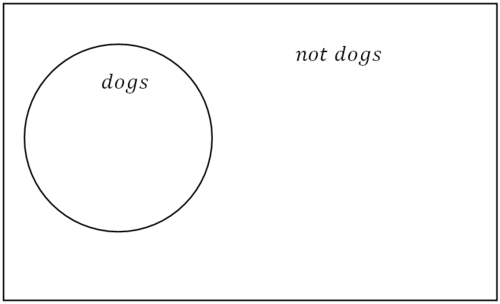Figura\(\PageIndex{1}\)Para negar declaraciones complejas que involucren conectivos lógicos como o, y, o sif-entonces, debe comenzar construyendo una tabla de verdad y señalando que la negación cambia completamente el valor de la verdad.
La negación de una declaración condicional sólo es verdadera cuando la declaración original if-then es falsa.
| \(P\) | \(Q\) | \(P \rightarrow Q\) | \(\sim (P \rightarrow Q)\) |
| T | T | T | F |
| T | F | F | T |
| F | T | T | F |
| F | F | T | F |
La negación de una conjunción sólo es falsa cuando las dos declaraciones originales son ambas verdaderas. Una conjunción son dos declaraciones a las que se unen un “y”.
| \(P\) | \(Q\) | \(P \wedge Q\) | \(\sim (P \wedge Q)\) |
| T | T | T | F |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
La negación de una disyunción sólo es cierta cuando ambas declaraciones originales son falsas. Una disyunción son dos declaraciones a las que se unen una “o”.
| \(P\) | \(Q\) | \(P \lor Q\) | \(\sim (P \lor Q)\) |
| T | T | T | F |
| T | F | T | F |
| F | T | T | F |
| F | F | F | T |
Los círculos de teoría de conjuntos también se pueden usar para interpretar la negación de una disyunción o una conjunción.
La porción sombreada en la caja representa el área que está dentro\(P\) o dentro\(Q\). Recordemos que en la lógica matemática, esto se escribe como\(P \lor Q\). En la teoría de conjuntos esta área se representa de manera similar a\(P \cup Q\) donde el símbolo\(\cup\) significa unión. Si bien la notación es ligeramente diferente, el razonamiento sobre las relaciones e implicaciones es idéntico.
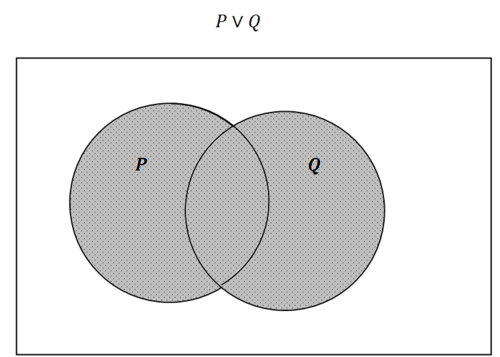Figura\(\PageIndex{2}\)Cuando niegas la declaración, cambias completamente lo que está sombreado.
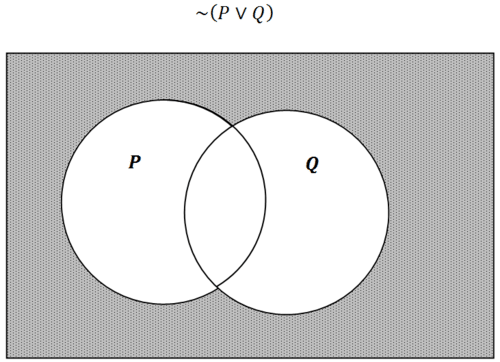Figura\(\PageIndex{3}\)Una manera diferente de pensar sobre esta región sombreada es que es la región que no está en P y tampoco en Q. Esto significa que\(\sim (P \lor Q)\) es equivalente a\(\sim P \wedge \sim Q\).
\(\sim (P \lor Q)\Leftrightarrow \sim P \wedge \sim Q\)
El símbolo “\(\Leftrightarrow\)” funciona en lógica matemática y teoría de conjuntos de la misma manera “\(=\)” funciona en aritmética y álgebra. En este caso, el negativo parece distribuirse a lo largo de la declaración o al negar cada declaración individualmente y cambia la declaración o a una declaración y. A esto se le llama Ley De Morgan.
La negación de una conjunción da un resultado similar.
La porción sombreada en la caja representa el área que está dentro de P y dentro\(Q\). En la lógica matemática esto se escribe como\(P \wedge Q\). En la teoría de conjuntos, esta área se representa de manera similar a\(P \cap Q\) donde el símbolo\(\cap\) representa intersección. Como antes, la notación entre la lógica matemática y la teoría de conjuntos es ligeramente diferente. Sin embargo, el razonamiento sobre las relaciones y las implicaciones lógicas son idénticos.
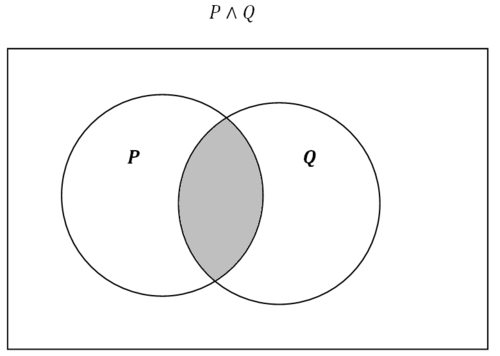Figura\(\PageIndex{4}\)Cuando niegas la declaración, cambias completamente lo que está sombreado.
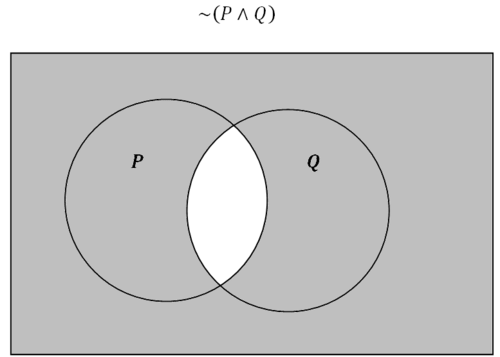Figura\(\PageIndex{5}\)Una manera diferente de pensar sobre esta región sombreada es considerar que representa todo lo que no está\(P\) o no está en\(Q\).
\(\sim (P \wedge Q) \Leftrightarrow \sim P \lor \sim Q\)
Esta es una segunda representación de la Ley de De Morgan.
A medida que las oraciones matemáticas se vuelven más complejas con conectivos adicionales, las tablas de verdad y los círculos de teoría de conjuntos son buenas formas de interpretar cuando las afirmaciones son verdaderas y cuando las afirmaciones son falsas.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó cuándo es cierta la negación de la siguiente afirmación.
Si no tengo frío, entonces no está nevando.
El enunciado ya tiene varias partes negativas, por lo que es incorrecto simplemente cambiar una o ambas de las negaciones.
- \(P=I\: am\: cold.\)
- \(Q=It\: is\: snowing.\)
Solución
| \(P\) | \(Q\) | \(\sim P\) | \(\sim Q\) | \(\sim P \rightarrow \sim Q\) | \(\sim ( \sim P \rightarrow \sim Q)\) |
| T | T | F | F | T | F |
| T | F | F | T | T | F |
| F | T | T | F | F | T |
| F | F | T | T | T | F |
Comience por construir hasta el estado de cuenta original. Después, agrega una columna que niega por completo la declaración original. Observe que sólo hay una fila donde la declaración negada final es verdadera. Ahí es cuando\(P\) es falso y\(Q\) es cierto. Por lo tanto, la negación de la frase original es cierta cuando “no tengo frío” y “está nevando”.
Ejemplo\(\PageIndex{2}\)
Use círculos de teoría de conjuntos para interpretar la negación de una declaración condicional y explicar cómo la negación de un condicional puede escribirse de una manera diferente.
Solución
La porción sombreada en el cuadro representa el área que hace verdadera la siguiente declaración.
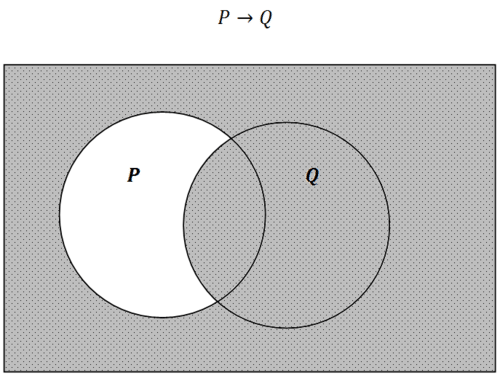Figura\(\PageIndex{6}\)Observe que hay cuatro regiones diferentes en el Diagrama de Venn que corresponden a las cuatro filas diferentes de la tabla de verdad condicional. El único espacio que no hace que la afirmación sea verdadera es cuando\(P\) es verdadera (círculo interior\(P\)) y\(Q\) es falso (círculo exterior\(Q\)).
| \(P\) | \(Q\) | \(P \rightarrow Q\) |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Para negar esta afirmación, cambia los valores en la tabla de verdad y cambia la región sombreada en el Diagrama de Venn.
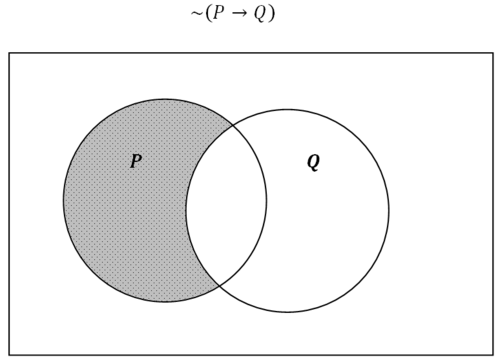Figura\(\PageIndex{7}\)Una manera diferente de pensar sobre esta región sombreada es verla como el espacio en el que se encuentra\(P\) pero no en\(Q\).
\(\sim (P \rightarrow Q) \Leftrightarrow P \wedge \sim Q\)
Ejemplo\(\PageIndex{3}\)
Demostrar que las siguientes afirmaciones son equivalentes en una tabla de verdad. El símbolo\(\equiv\) significa equivalente. Ser equivalente en este caso significa ser verdadero al mismo tiempo y falso al mismo tiempo.
\(P \wedge Q \equiv \sim ( \sim P \lor \sim Q)\)
Solución
Si bien una tabla de verdad no es una prueba, puede ayudarte a reconocer cuando dos afirmaciones tienen los mismos valores de verdad.
| \(P\) | \(Q\) | \(\sim P\) | \(\sim Q\) | \(\sim P \lor \sim Q\) | \(\sim ( \sim P \lor \sim Q)\) | \(P \wedge Q\) |
| T | T | F | F | F | T | T |
| T | F | F | T | T | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | T | F | F |
Observe que las dos columnas finales son idénticas.
Ejemplo\(\PageIndex{4}\)
Escribir una oración de dos maneras diferentes que ilustren la declaración matemática en el Ejemplo 3
Solución
\(P \wedge Q\): Me gustan las películas y me gusta la televisión. \(\sim ( \sim P \lor \sim Q)\): No es el caso que o no me gustan las películas o no me gusta la televisión.
Ejemplo\(\PageIndex{5}\)
Una tautología es una afirmación lógica que siempre es cierta. Demostrar la siguiente tautología en una tabla de verdad.
\(B \rightarrow (A \lor \sim A)\)
Solución
| \(A\) | \(\sim A\) | \(B\) | \(A \lor \sim A\) | \(B \rightarrow (A \lor \sim A)\) |
| T | F | F | T | T |
| T | F | T | T | T |
| F | T | T | T | T |
| F | T | F | T | T |
Observe que la última columna es toda T's. Esto quiere decir que esta afirmación es siempre cierta y por lo tanto es una tautología.
Revisar
O voy a esquiar o hacer snowboard el próximo fin de semana.
1. Identificar las declaraciones atómicas en la oración anterior y usar conectivos lógicos para reescribir la oración con símbolos.
2. Escribe la negación de la oración con símbolos y escribe la negación de la oración en palabras de manera natural.
Mike y John almorzaron conmigo.
3. Identificar las declaraciones atómicas en la oración anterior y usar conectivos lógicos para reescribir la oración con símbolos.
4. Escribe la negación de la oración con símbolos y escribe la negación de la oración en palabras de manera natural.
Ni mi hermano ni mi hermana quieren jugar conmigo.
5. Identificar las declaraciones atómicas en la oración anterior y usar conectivos lógicos para reescribir la oración con símbolos.
6. Escribe la negación de la oración con símbolos y escribe la negación de la oración en palabras de manera natural.
Escribir negaciones para las siguientes declaraciones.
7. Todos los perros van al cielo.
8. Mi maestro rara vez se equivoca.
9. A todos les gusta la pizza.
Hacer tablas de verdad para cada una de las siguientes.
10. \((P \wedge Q) \lor \sim Q\)
11. \(P \wedge (Q \lor \sim Q)\)
12. \((P \lor Q) \lor \sim R\)
13. \(( \sim P \wedge \sim Q) \lor \sim R\)
14. ¿Cuál es la afirmación más simple que equivale a #11:\(P \wedge (Q \lor \sim Q)\)?
15. Use la Ley de De Morgan para encontrar una declaración equivalente a la siguiente declaración:\(\sim (Q \lor \sim Q)\)
16. Use la Ley de De Morgan para encontrar una declaración equivalente a la siguiente declaración:\(\sim (P \lor Q) \lor \sim R\)
El vocabulario
| Término | Definición |
|---|---|
| declaración atómica | Una declaración atómica es una declaración declarativa sin conectivos lógicos que tiene un valor de verdad. |
| conjunción | Una conjunción es una declaración “y”, que es una declaración que combina dos declaraciones lógicas y sólo es verdadera cuando ambas declaraciones son verdaderas. El símbolo para “y” es “\(\wedge\)”. |
| Ley de Morgan | La ley de De Morgan transforma una conjunción en una disyunción mediante la negación. |
| disyunción | Una disyunción es una declaración “o” que combina dos declaraciones lógicas, y solo es falsa cuando ambas declaraciones son falsas. El símbolo para “o” es “\(\lor\)”. |
| negación | La negación de una declaración es lo contrario de la declaración. Si la declaración original es\(D\), entonces la negación de la declaración está representada por\(\sim D\). Una declaración y su negación siempre tendrán valores de verdad opuestos. |
| tautología | Una tautología es una afirmación lógica que siempre es cierta. Una tautología es un tipo de teorema básico. |
Recurso Adicional
Práctica: Declaraciones negativas