1.4: Aplicaciones Usando el Teorema de Pitágoras

Última actualización
Guardar como PDF

Page ID: 107680

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Problemas de palabras usando el Teorema de Pitágoras

El Teorema de Pitágoras y su contrario tienen muchas aplicaciones para encontrar longitudes y distancias.

Aplicación en el mundo real: longitud diagonal

María tiene una hoja rectangular para galletas que mide 10 pulgadas×14 pulgadas. Encuentra la longitud de la diagonal de la hoja para galletas.

Dibuja un boceto:

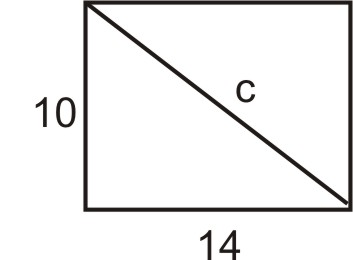
f-d_a5132a90081d190373037b8a932893346d82a897cb53a469e88bf7c6+image_tiny+image_tiny.png — Figura\(\PageIndex{1}\)

Definir variables: Let\(c= \text{ length of the diagonal}\).

Escribe una fórmula: Usa el Teorema de Pitágoras:\(a^2+b^2=c^2\)

Resuelve la ecuación:

\(\begin{aligned} 10^2+14^2&=c^2 \\ 100+196&=c^2 \\ c^2&=296 \Rightarrow c=\sqrt{296} \Rightarrow c=2 \sqrt{74} \text{ or } c=17.2 \text{ inches } \end{aligned}\)

Cheque:\(10^2+14^2=100+196=296\) y\(c^2=17.2^2=296\). La solución comprueba.

Aplicación en el mundo real: Área de regiones sombreadas

Encuentra el área de la región sombreada en el siguiente diagrama:

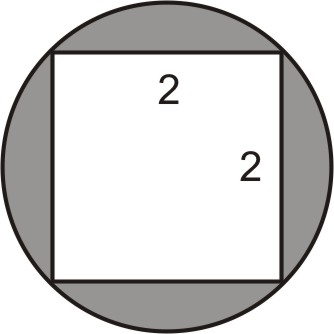
f-d_de048c8f31ef804baf146f1f84d7204fa82dc4ef6b3434ee29310df7+image_tiny+image_tiny.png — Figura\(\PageIndex{2}\)

Dibuja la diagonal del cuadrado en la figura:

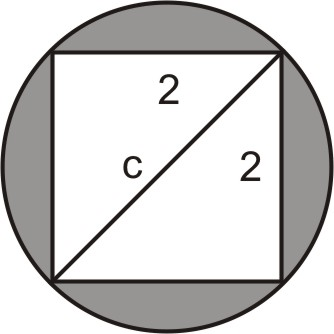
f-d_e1250690c3e1e1eb0db4ad990c5a283d95c50402eee1fd6bf1e539e2+image_tiny+imagen_tiny.png — Figura\(\PageIndex{3}\)

Observe que la diagonal del cuadrado es también el diámetro del círculo.

Definir variables: Let\(c= \text{ diameter of the circle}\).

Escribe la fórmula: Usa el Teorema de Pitágoras:\(a^2+b^2=c^2\).

Resuelve la ecuación:

\(\begin{aligned} 2^2+2^2&=c^2 \\ 4+4&=c^2 \\ c^2&=8 \Rightarrow c=\sqrt{8} \Rightarrow c=2\sqrt{2}\end{aligned}\)

El diámetro del círculo es\(2\sqrt{2}\), por lo tanto, el radio\(R=\sqrt{2}\).

Área de un círculo fórmula:\(A= \pi \cdot R^2=\pi (\sqrt{2})^2=2\pi\).

Por lo tanto, el área de la región sombreada es\(2\pi−4=2.28\).

Aplicación en el mundo real: Medición de los lados de un triángulo

En un triángulo rectángulo, una pata es el doble de larga que la otra y el perímetro es 28. ¿Cuáles son las medidas de los lados del triángulo?

Hacer un boceto y definir variables:

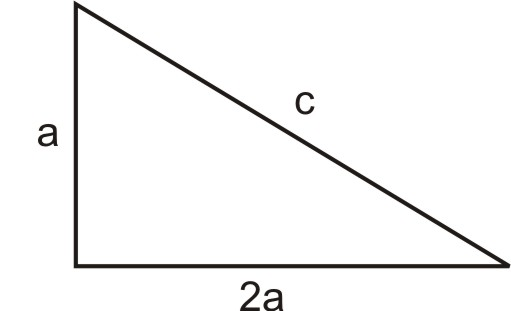
f-d_c87244233d16961ad4cea96db8615893ee8c67dcb5e0a33314a85f4f+image_tiny+image_tiny.png — Figura\(\PageIndex{4}\)

Dejar:\(a= \text{ length of the short leg}\)

\(2a= \text{ length of the long leg }\)

\(c= \text{ length of the hypotenuse}\)

Escribir fórmulas:

Los lados del triángulo están relacionados de dos maneras diferentes.

El perímetro es 28, entonces\(a+2a+c=28 \Rightarrow 3a+c=28\)

El triángulo es un triángulo rectángulo, por lo que las medidas de los lados deben satisfacer el Teorema de Pitágoras:

\(\begin{aligned} a^2+(2a)^2&=c^2 \Rightarrow a^2+4a^2=c^2 \Rightarrow 5a^2=c^2 \\ \text{ or } \qquad c&=a\sqrt{5}=2.236a\end{aligned}\)

Resuelve la ecuación:

Enchufe el valor de c que acabamos de obtener en la ecuación perimetral:\(3a+c=28\)

\(3a+2.236a=28 \Rightarrow 5.236a=28 \Rightarrow a=5.35\)

La pierna corta es:\(a=5.35\)

La pierna larga es:\(2a=10.70\)

La hipotenusa es:\(c=11.95\)

Comprobar: Las patas del triángulo deben satisfacer el Teorema de Pitágoras:

\(a^2+b^2=5.35^2+10.70^2=143.1\),\(c^2=11.95^2=142.80\). Los resultados son aproximadamente los mismos.

El perímetro del triángulo debe ser 28:

\(a+b+c=5.35+10.70+11.95=28\). La respuesta se comprueba.

Ejemplo\(\PageIndex{1}\)

Mike está cargando una camioneta en movimiento caminando por una rampa. La rampa mide 10 pies de largo y la cama de la camioneta está a 2.5 pies sobre el suelo. ¿Hasta dónde se extiende la rampa más allá de la parte trasera de la camioneta?

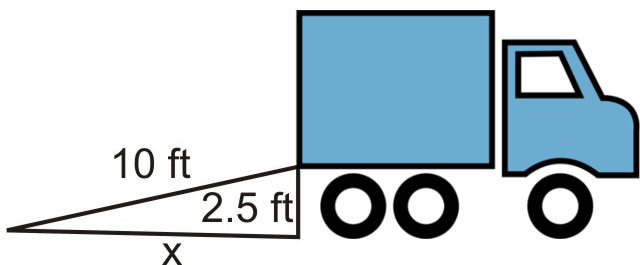
f-d_bf179c871b4b693fadc2e68bcff45f60559d6680af4312277a98624e+image_tiny+image_tiny.png — Figura\(\PageIndex{5}\)

Solución

Definir variables: Let\(x= \text{ how far the ramp extends past the back of the van }\).

Escribe una fórmula: Usa el Teorema de Pitágoras:\(x^2+2.5^2=10^2\)

Resuelve la ecuación:

\(\begin{aligned}x^2+6.25&=100 \\ x^2&=93.5 \\ x&=\sqrt{93.5}=9.7\text{ ft }\end{aligned}\)

Verifique tapando el resultado en el Teorema de Pitágoras:

\(9.7^2+2.5^2=94.09+6.25=100.34 \approx 100\). Entonces la rampa mide 10 pies de largo. La respuesta se comprueba.

Revisar

Para hacer una rampa que sea\(3 \text{ ft}\) alta y cubiertas\(4 \text{ ft}\) de suelo, ¿cuánto tiempo debe durar la rampa?
Un diamante de béisbol de regulación es un cuadrado con 90 pies entre bases. ¿A qué distancia está la segunda base del plato casero?
Emanuel tiene una caja de cartón que mide\(20 \text{ cm long } \times 10 \text{ cm wide }\times 8 \text{ cm deep }\).
1. ¿Cuál es la longitud de la diagonal en la parte inferior de la caja?
2. ¿Cuál es la longitud de la diagonal desde una esquina inferior hasta la esquina superior opuesta?
Samuel coloca una escalera contra su casa. La base de la escalera está a 6 pies de la casa y la escalera mide 10 pies de largo.
1. ¿Qué tan alto sobre el suelo toca la escalera la pared de la casa?
2. Si el borde del techo está a 10 pies del suelo y se destaca 1.5 pies más allá de la pared, ¿qué tan lejos está desde el borde del techo hasta la parte superior de la escalera?
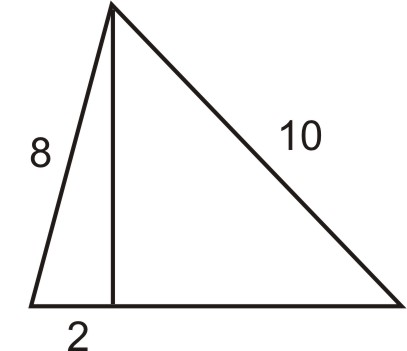
Encuentre el área del triángulo debajo si el área de un triángulo se define como\(A=\dfrac{1}{2} \text{ base } \times \text{ height}\):

Figura\(\PageIndex{6}\)
En lugar de caminar por los dos lados de un campo rectangular, Mario decidió cortar a través de la diagonal. Se ahorra así una distancia que es la mitad del lado largo del campo.
1. Encuentra la longitud del lado largo del campo dado que el lado corto es de 123 pies.
2. Encuentra la longitud de la diagonal.
Marcus navega hacia el norte y Sandra navega hacia el este desde el mismo punto de partida. En dos horas el barco de Marcus está a 35 millas del punto de partida y el barco de Sandra está a 28 millas del punto de partida.
1. ¿A qué distancia están los barcos el uno del otro?
2. Sandra luego navega 21 millas con rumbo al norte mientras Marcus se queda quieto. ¿A qué distancia está Sandra del punto de partida original?
3. ¿A cuánta distancia está Sandra de Marcus ahora?
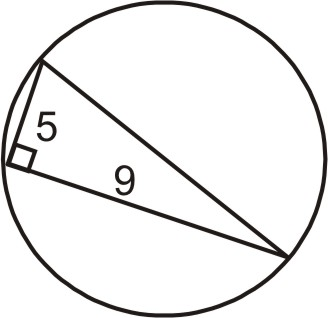
Determine el área del círculo a continuación. (Pista: la hipotenusa del triángulo es el diámetro del círculo.)

Figura\(\PageIndex{7}\)
La longitud de un rectángulo es\(1 \text{ in}\) más larga que su anchura y la diagonal tiene una longitud de\(29 \text{ in}\). ¿Cuáles son las longitudes de los lados del rectángulo?
Para un triángulo isósceles con lados de la longitud dada, encuentra la longitud de cada hipotenusa:
1. 1
2. 2
3. 3
4. \(n\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.10.

El vocabulario

Término	Definición
converse	Si una declaración condicional es\(p\rightarrow q\) (si\(p\), entonces\(q\)), entonces lo contrario es\(q \rightarrow p\) (si\(q\), entonces\(p\)). Tenga en cuenta que lo contrario de una declaración no es cierto solo porque la declaración original es verdadera.

Recursos adicionales

Video: Resolviendo problemas de palabras que involucran raíces cuadradas - Descripción general

Práctica: Aplicaciones usando el teorema de Pitágoras