2.3.4: Ángulos coterminales

Última actualización
Guardar como PDF

Page ID: 107669

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Conjunto de ángulos con el mismo terminal o lado final.

Mientras juegas un juego con amigos, usas un spinner que se ve así:

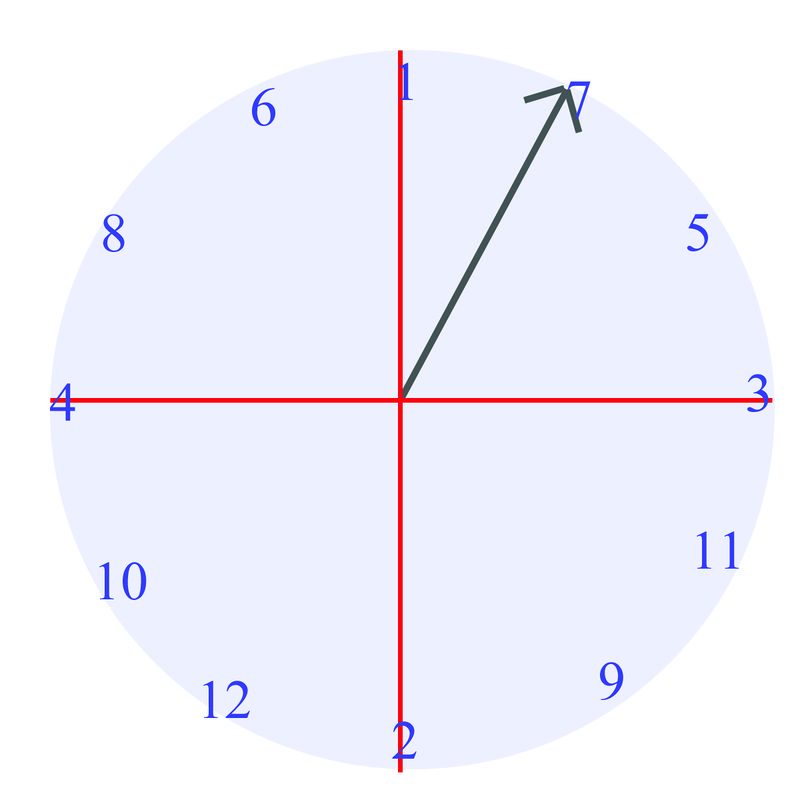
F-d_f7240c6d67dc4c11a91ef52a9bd37ee4fffeff6e8b3f1b75cad23ab6+image_tiny+image_tiny.jpg — Figura\(\PageIndex{1}\)

Como puedes ver, el ángulo que hace el spinner con la horizontal es\(60^{\circ}\). ¿Es posible representar el ángulo de otra manera?

Ángulos coterminales

Considera el ángulo\(30^{\circ}\), en posición estándar.

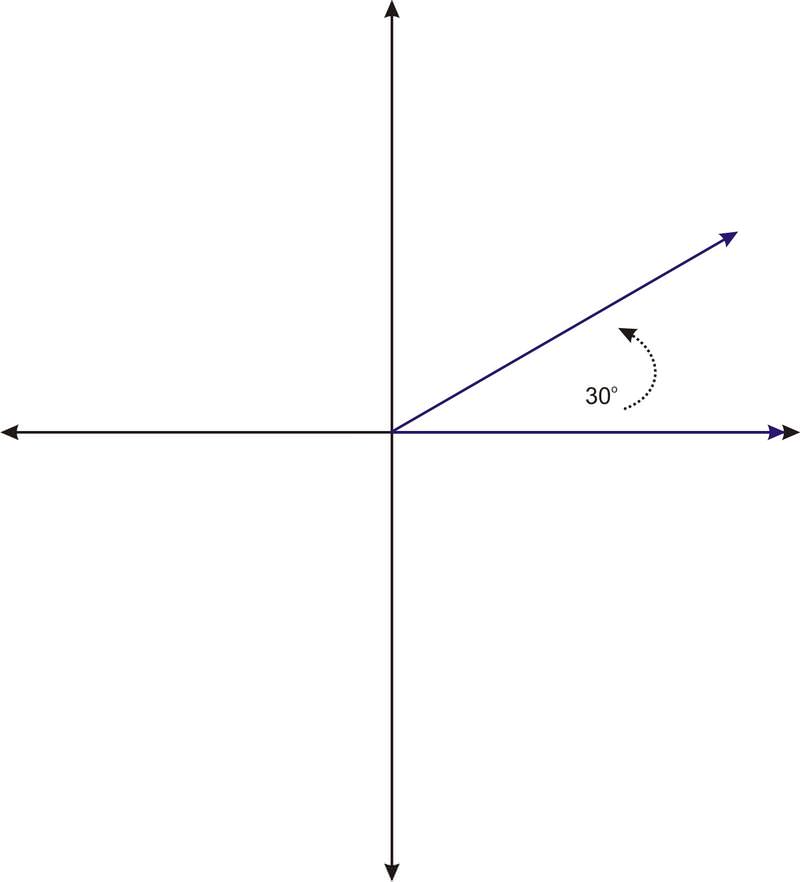
f-d_bf84fee1daaa9b351764625d762ccde992c539f0991bc0c27057a764+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

Ahora considera el ángulo\(390^{\circ}\). Podemos pensar en este ángulo como una rotación completa (\(360^{\circ}\)), más 30 grados adicionales.

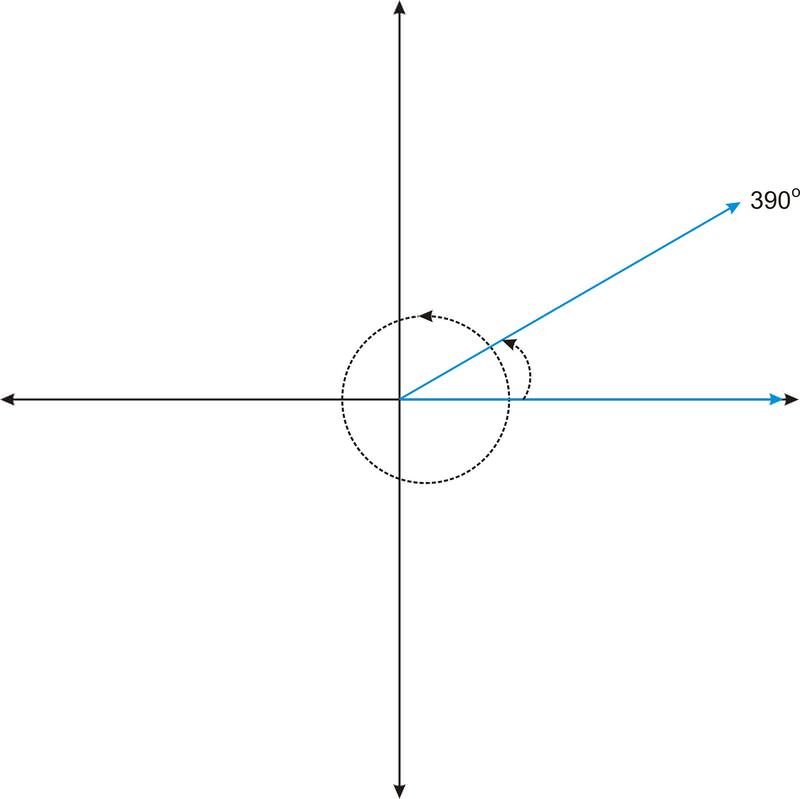
f-d_1d389b6f5ea40c5442bde599b63f42ab1653590f787828e2395c5057+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

Observe que\(390^{\circ}\) se ve igual que\(30^{\circ}\). Formalmente, decimos que los ángulos comparten el mismo lado terminal. Por lo tanto llamamos a los ángulos coterminales. No sólo estos dos ángulos son co-terminales, sino que hay infinitamente muchos ángulos que son co-terminales con estos dos ángulos. Por ejemplo, si giramos otro\(360^{\circ}\), obtenemos el ángulo\(750^{\circ}\). O bien, si creamos el ángulo en la dirección negativa (en sentido horario), obtenemos el ángulo\(−330^{\circ}\). Debido a que podemos rotar en cualquier dirección, y podemos rotar tantas veces como queramos, podemos generar continuamente ángulos que son co-terminales con\(30^{\circ}\).

Identificación de ángulos coterminales

Para las siguientes preguntas, determine si el ángulo es co-terminal con\(45^{\circ}\).

1. \(−45^{\circ}\)

No, no es co-terminal con\(45^{\circ}\)

2. \(405^{\circ}\)

Sí,\(405^{\circ}\) es co-terminal con\(45^{\circ}\).

3. \(−315^{\circ}\)

Sí,\(−315^{\circ}\) es co-terminal con\(45^{\circ}\).

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le preguntó si es posible representar el ángulo de otra manera.

Solución

Puedes pensar en\(60^{\circ}\) como\(420^{\circ}\) si gieras todo el círculo una vez y continúas la rotación hasta donde se ha detenido el spinner, o como\(−300^{\circ}\) si giraras en el sentido de las agujas del reloj alrededor del círculo en lugar de en sentido antihorario hasta donde se ha detenido el spinner.

Ejemplo\(\PageIndex{2}\)

Encuentra un ángulo coterminal para\(23^{\circ}\)

Solución

Un ángulo coterminal sería un ángulo que se encuentra en el mismo lugar terminal que\(23^{\circ}\) pero que tiene un valor diferente. En este caso,\(−337^{\circ}\) es un ángulo coterminal.

Ejemplo\(\PageIndex{3}\)

Encuentra un ángulo coterminal para\(−90^{\circ}\)

Solución

Un ángulo coterminal sería un ángulo que está en el mismo lugar terminal que −90^ {\ circ}\) pero tiene un valor diferente. En este caso,\(270^{\circ}\) es un ángulo coterminal.

Ejemplo\(\PageIndex{4}\)

Encuentra dos ángulos coterminales a\(70^{\circ}\) girando en la dirección positiva alrededor del círculo.

Solución

Girar una vez alrededor del círculo da un ángulo coterminal de\(430^{\circ}\). Girar de nuevo alrededor del círculo da un ángulo coterminal de\(790^{\circ}\).

Revisar

¿Es\(315^{\circ}\) co-terminal con\(−45^{\circ}\)?
¿Es\(90^{\circ}\) co-terminal con\(−90^{\circ}\)?
¿Es\(350^{\circ}\) co-terminal con\(−370^{\circ}\)?
¿Es\(15^{\circ}\) co-terminal con\(1095^{\circ}\)?
¿Es\(85^{\circ}\) co-terminal con\(1880^{\circ}\)?

Para cada diagrama, nombra el ángulo de 3 maneras. Al menos una forma debe usar grados negativos.

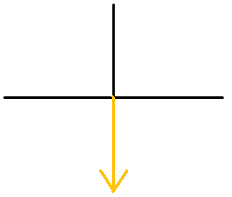
Figura\(\PageIndex{4}\)
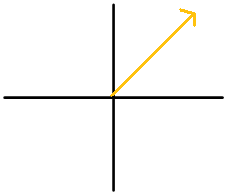
Figura\(\PageIndex{5}\)
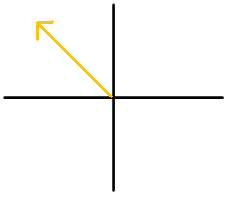
Figura\(\PageIndex{6}\)
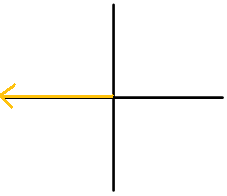
Figura\(\PageIndex{7}\)
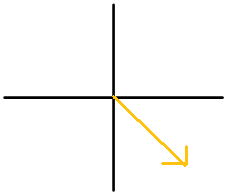
Figura\(\PageIndex{8}\)
Nombra el ángulo del 8 en un reloj estándar de dos maneras diferentes.
Nombra el ángulo del 11 en un reloj estándar de dos maneras diferentes.
Nombra el ángulo del 4 en un reloj estándar de dos maneras diferentes.
Explicar cómo determinar si dos ángulos son o no co-terminales.
¿Cuántas rotaciones hay\(4680^{\circ}\)?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.16.

vocabulario

Término	Definición
Ángulos coterminales	Un conjunto de ángulos coterminales son ángulos con el mismo lado terminal pero expresados de manera diferente, como un número diferente de rotaciones completas alrededor del círculo unitario o ángulos que se expresan como mediciones de ángulo positivo versus negativo.

Recursos adicionales

Elemento Interactivo

Video: Ejemplo: Determine si dos ángulos son coterminales

Práctica: Ángulos coterminales