4.2.5: Soluciones Generales de Triángulos
- Page ID
- 107606
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aplicación del teorema de pitágoras, funciones trigonométricas y leyes de los senos/cosenos.
Mientras platicas un día con tu hermanita, la conversación se convierte en formas. Tu hermana sólo está en la secundaria, así que si bien sabe algunas cosas sobre los triángulos rectos, como el Teorema de Pitágoras, no sabe nada de otro tipo de triángulos. Le muestras un ejemplo de triángulo oblicuo dibujando esto en una hoja de papel:
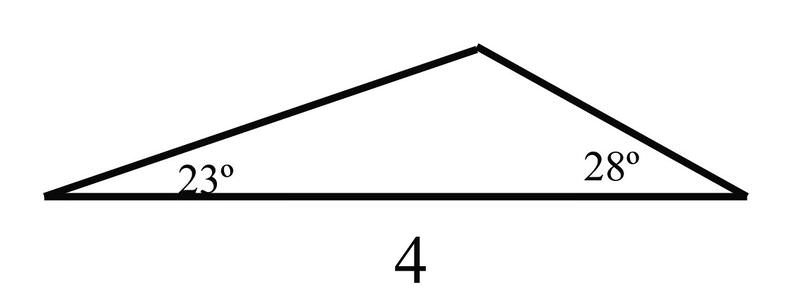
Fascinada, te dice que sabe calcular el área de un triángulo usando la fórmula familiar\(\dfrac{1}{2} bh\) y las longitudes de los lados si el triángulo es un triángulo rectángulo, pero que no puede usar las fórmulas en el triángulo que acabas de dibujar.
“¿Sabes cómo encontrar las longitudes de los lados del triángulo y el área?” ella pregunta.
Encontrar soluciones para triángulos
Encontrar los lados, ángulos y área para triángulos rectos a menudo se aprende en Álgebra y/o Geometría. Sin embargo, es común aprender a determinar esta información en triángulos no rectos en Trigonometría.
A continuación se muestra una tabla que resume
común
técnicas triangulares. Esta tabla describe el tipo de triángulo (ya sea derecho u oblicuo), la información dada, la técnica apropiada a utilizar y lo que podemos encontrar usando cada técnica.
| Tipo de Triángulo: | Información dada: | Técnica: | Lo que podemos encontrar: |
|---|---|---|---|
| Derecha | Dos lados | Teorema de Pitágoras | Tercer lado |
| Derecha | Un ángulo y un lado | Relaciones trigonométricas | Cualquiera de los otros dos lados |
| Derecha | Dos lados | Relaciones trigonométricas | Cualquiera de los otros dos ángulos |
| Oblicua | 2 ángulos y un lado no incluido (AAS) | Ley de los Sines | El otro lado no incluido |
| Oblicua | 2 ángulos y el lado incluido (ASA) | Ley de los Sines | Cualquiera de los lados no incluidos |
| Oblicua | 2 lados y el ángulo opuesto a uno de esos lados (SSA) — Caso ambiguo | Ley de los Sines | El ángulo opuesto al otro lado (no puede producir ninguna, una o dos soluciones) |
| Oblicua | 2 lados y el ángulo incluido (SAS) | Ley de Cosinos | El tercer lado |
| Oblicua | 3 lados | Ley de Cosinos | Cualquiera de los tres |
| ángulos |
Resolviendo triángulos
1. En\(\Delta ABC\),\(a=12\),\(b=13\),\(c=8\). Resuelve el triángulo.
Ya que nos dan los tres lados en el triángulo, podemos usar la Ley de Cosinos. Antes de que podamos resolver el triángulo, es importante saber qué información nos falta. En este caso, no conocemos ninguno de los ángulos, así que estamos resolviendo para\(\angle A\),\(\angle B\), y\(\angle C\). Comenzaremos por encontrar\(\angle A\):
\(\begin{aligned} 12^2 &=8^2+13^2−2(8)(13)\cos A\\ 144 &=233−208\cos A\\ −89 &=−208\cos A\\ 0.4278846154&=\cos A\\ 64.7&\approx \angle A \end{aligned}\)
Ahora, encontraremos\ ángulo B usando la Ley de Cosinos. Ten en cuenta que ahora también puedes usar la Ley de los Sinos para encontrar\(\angle B\). Usa cualquier método con el que te sientas más cómodo.
\(\begin{aligned} 13^2 &=8^2+12^2−2(8)(12) \cos B\\ 169 &=208−192\cos B\\ −39 &=−192\cos B\\ 0.2031 &=\cos B\\ 78.3^{\circ} & \approx \angle B \end{aligned}\)
Ahora podemos encontrar rápidamente\(\angle C\) usando el Teorema de la Suma del Triángulo,
\(180^{\circ} −64.7^{\circ} −78.3^{\circ} =37^{\circ}\)
2. En triángulo\(DEF\),\(d=43\),\(e=37\), y\(\angle F=124^{\circ} \). Resuelve el triángulo.
En este triángulo, tenemos el caso SAS porque conocemos dos lados y el ángulo incluido. Esto significa que podemos usar la Ley de Cosinos para resolver el triángulo. Para resolver este triángulo, necesitamos encontrar lado\(f\),\(\angle D\), y\(\angle E\). Primero, necesitaremos encontrar lado\(f\) usando la Ley de Cosinos.
\ (\ begin {alineado}
f^ {2} &=43^ {2} +37^ {2} -2 (43) (37)\ cos 124\\
f^ {2} &=4997.351819\\
f &\ aproximadamente 70.7
\ end {alineado}\)
Ahora que sabemos\(f\), conocemos los tres lados del triángulo. Esto significa que podemos usar la Ley de Cosinos para encontrar cualquiera\(\angle D\) o\(\angle E\). Lo encontraremos\(\angle D\) primero.
\ (\ begin {alineado}
43^ {2} &=70.7^ {2} +37^ {2} -2 (70.7) (37)\ cos D\\
1849 &=6367.49-5231.8\ cos D\\
-4518.49 &=-5231.8\ cos D\\
0.863658779 &=\ cos D\\
30.3^ {\ circ} &\ approx\ ángulo D
\ final {alineado}\)
Para encontrar\(\angle E\), sólo necesitamos usar el Teorema de la Suma del Triángulo,\(\angle E=180−(124+30.3)=25.7^{\circ} \).
3. En triángulo\(ABC\),\(A=43^{\circ} \),\(B=82^{\circ} \), y\(c=10.3\). Resuelve el triángulo.
Este es un ejemplo del caso ASA, lo que significa que podemos usar la Ley de Sines para resolver el triángulo. Para poder utilizar la Ley de Sines, primero debemos saber\(\angle C\), que podemos encontrar usando el Teorema de la Suma del Triángulo,\(\angle C=180^{\circ} −(43^{\circ} +82^{\circ} )=55^{\circ} \).
Ahora que sabemos\(\angle C\), podemos usar la Ley de los Sinos para encontrar cualquiera de los lados a o lados\(b\).
\ (\ comenzar {alineado}
\ frac {\ sin 55} {10.3} & =\ frac {\ sin 43} {a} &\ frac {\ sin 55} {10.3} & =\ frac {\ sin 82} {b}\\
a & =\ frac {10.3\ sin 43} {\ sin 55} & b & =\ frac {10.3\ sin 82} {sin 55}\\
a & =8.6 & b & =12.5
\ end {alineado}\)
Anteriormente, te preguntaron cómo podrías ayudar a tu hermana a encontrar las longitudes de los lados y el área de un triángulo no rectángulo.
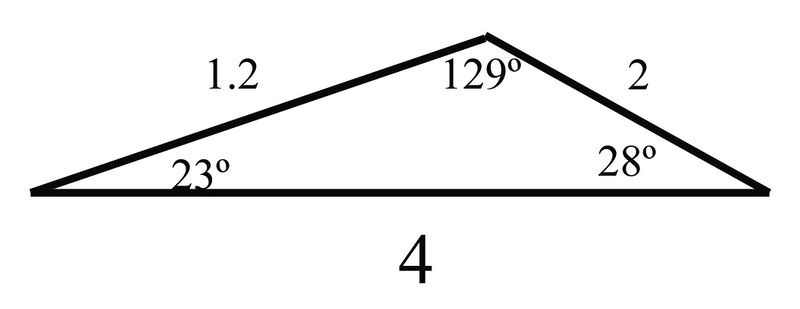
Solución
Ya que sabes que dos de los ángulos son\(23^{\circ} \) y\(28^{\circ} \), el tercer ángulo en el triángulo debe ser\(180^{\circ} −23^{\circ} −28^{\circ} =129^{\circ} \). Usando estos ángulos y el conocimiento de que uno de los lados tiene una longitud de 4, puedes resolver para las longitudes de los otros dos lados usando la Ley de Sines:
\(\begin{aligned} \dfrac{\sin A}{a}&=\dfrac{\sin B}{b} \\ \dfrac{\sin 23^{\circ} }{a}&=\dfrac{\sin 129^{\circ} }{4} \\ a&=\dfrac{4 \sin 23^{\circ} }{\sin 129^{\circ} }=\dfrac{1.56}{.777} \\ a&\approx 2 \end{aligned}\)
Y repitiendo el proceso para la tercera cara:
\(\begin{aligned} \dfrac{\sin A}{a}&=\dfrac{\sin C}{c} \\ \dfrac{\sin 23^{\circ} }{2}&= \dfrac{\sin 28^{\circ} }{c} \\ c&=\dfrac{2\sin 28^{\circ} }{\sin 23^{\circ} }=\dfrac{.939}{.781} \\ c&\approx 1.2 \end{aligned}\)
Ahora ya conoces los tres ángulos y los tres lados. Puedes usar la fórmula de Heron o la fórmula alternativa para el área de un triángulo para encontrar el área:
\(\begin{aligned} K&=\dfrac{1}{2} bc\sin A \\ K&=\dfrac{1}{2} (4)(1.2)\sin 23^{\circ} \\K&=\dfrac{1}{2}(4)(1.2)(.391) \\ K&\approx .9384 \end{aligned}\)
Utilizando la información proporcionada, decide en qué caso te dan (SSS, SAS, AAS, ASA o SSA), y si utilizarías la Ley de Sines o la Ley de Cosinos para encontrar el lado o ángulo solicitado. Hacer un dibujo aproximado del triángulo y etiquetar la información dada. También, indique cuántas soluciones (si las hubiera) tendría el triángulo. Si un triángulo no tiene solución o dos soluciones, explique por qué.
Solución
\(A=69^{\circ} \),\(B=12^{\circ} \),\(a=22.3\), encontrar\(b\)
AAS, Ley de Senos, una solución
Utilizando la información proporcionada, decide en qué caso te dan (SSS, SAS, AAS, ASA o SSA), y si utilizarías la Ley de Sines o la Ley de Cosinos para encontrar el lado o ángulo solicitado. Hacer un dibujo aproximado del triángulo y etiquetar la información dada. También, indique cuántas soluciones (si las hubiera) tendría el triángulo. Si un triángulo no tiene solución o dos soluciones, explique por qué.
Solución
\(a=1.4\),\(b=2.3\),\(C=58^{\circ} \), encontrar\(c\).
SAS, Ley de Cosinos, una solución
Utilizando la información proporcionada, decide en qué caso te dan (SSS, SAS, AAS, ASA o SSA), y si utilizarías la Ley de Sines o la Ley de Cosinos para encontrar el lado o ángulo solicitado. Hacer un dibujo aproximado del triángulo y etiquetar la información dada. También, indique cuántas soluciones (si las hubiera) tendría el triángulo. Si un triángulo no tiene solución o dos soluciones, explique por qué.
Solución
\(a=3.3\),\(b=6.1\),\(c=4.8\), encontrar\(A\).
SSS, Ley de Cosinos, una solución
Revisar
Utilizando la información proporcionada, decide en qué caso te dan (SSS, SAS, AAS, ASA o SSA), y si utilizarías la Ley de Sines o la Ley de Cosinos para encontrar el lado o ángulo solicitado. Hacer un dibujo aproximado del triángulo y etiquetar la información dada. También, indique cuántas soluciones (si las hubiera) tendría el triángulo.
- \(a=3\),\(b=4\),\(C=71^{\circ} \), encontrar\(c\).
- \(a=8\),\(b=7\),\(c=9\), encontrar\(A\).
- \(A=135^{\circ}\),\(B=12^{\circ} \),\(c=100\), encontrar\(a\).
- \(a=12\),\(b=10\),\(A=80^{\circ} \), encontrar\(c\).
- \(A=50^{\circ} \),\(B=87^{\circ}\),\(a=13\), encontrar\(b\).
- En\(\Delta ABC\),\(a=15\),\(b=19\),\(c=20\). Resuelve el triángulo.
- En\(\Delta DEF\),\(d=12\),\(E=39^{\circ}\),\(f=17\). Resuelve el triángulo.
- En\(\Delta PQR\),\(P=115^{\circ} \),\(Q=30^{\circ} \),\(q=10\). Resuelve el triángulo.
- En\(\Delta MNL\),\(m=5\),\(n=9\),\(L=20^{\circ} \). Resuelve el triángulo.
- En\(\Delta SEV\),\(S=50^{\circ} \),\(E=44^{\circ} \),\(s=12\). Resuelve el triángulo.
- En\(\Delta KTS\),\(k=6\),\(t=15\),\(S=68^{\circ} \). Resuelve el triángulo.
- En\(\Delta WRS\),\(w=3\),\(r=5\),\(s=6\). Resuelve el triángulo.
- En\(\Delta DLP\),\(D=52^{\circ}\),\(L=110^{\circ} \),\(p=8\). Resuelve el triángulo.
- En\(\Delta XYZ\),\(x=10\),\(y=12\),\(z=9\). Resuelve el triángulo.
- En\(\Delta AMF\),\(A=99^{\circ}\),\(m=1\),\(f=16\). Resuelve el triángulo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.12.
El vocabulario
| Término | Definición |
|---|---|
| ley de cosenos | La ley de los cosenos es una norma que relaciona los lados de un triángulo con el coseno de uno de sus ángulos. La ley de los cosenos establece que\(c^2=a^2+b^2−2ab\cos C\), dónde\(C\) está el ángulo a través de lado\(c\). |
| ley de los senos | La ley de los senos es una regla aplicada a los triángulos que establece que la relación del seno de un ángulo al lado opuesto a ese ángulo es igual a la relación del seno de otro ángulo en el triángulo al lado opuesto a ese ángulo. |
Recursos adicionales
Video: La ley de los senos: Lo básico
Práctica: Soluciones generales de triángulos

