4.2.4: Fórmula de Heron
- Page ID
- 107618
Fórmula de área basada en longitudes de lados de un triángulo y la mitad de su perímetro.
Sarine dibuja un triángulo y mide sus lados como 2 pulgadas, 5 pulgadas y 6 pulgadas. ¿Cuál es el área de su triángulo?
Fórmula de Heron
La Fórmula de Garza, que lleva el nombre de Héroe de Alejandría hace 2000 años, se puede utilizar para encontrar el área de un triángulo dadas las tres longitudes laterales. La fórmula requiere el semiperímetro,\(s\), o\(\dfrac{1}{2}(a+b+c)\), donde\(a\),\(b\) y\(c\) son las longitudes de los lados del triángulo.
Fórmula de Heron:
\(\text{Area}=\sqrt{s(s−a)(s−b)(s−c)}\)
Usemos la fórmula de Heron para encontrar el área de un triángulo con longitudes laterales de 13 cm, 16 cm y 23 cm.
Primero, encuentra el semiperímetro o\(s\):\(s=\dfrac{1}{2}(13+16+23)=26\). A continuación, sustituya nuestros valores en la fórmula como se muestra y evalúe:
\(A=\sqrt{26(26−13)(26−16)(26−23)}=\sqrt{26(13)(10)(3)}=\sqrt{10140}\approx 101 \text{ cm}^2\)
Ahora, respondamos a las siguientes preguntas.
- Alena está planeando un jardín en su patio. Ella está usando tres piezas de madera como borde. Si las piezas de madera tienen longitudes de 4 pies, 6 pies y 3 pies, ¿cuál es el área de su jardín?
El jardín será triangular con longitudes laterales de 4 pies, 6 pies y 3 pies. Encuentra el semiperímetro y luego usa la fórmula de Heron para encontrar el área.
\(\begin{aligned} s&=\dfrac{1}{2}(4+6+3)=\dfrac{13}{2} \\ A&=\sqrt{\dfrac{13}{2}\left(\dfrac{13}{2}−4\right)\left(\dfrac{13}{2}−6\right)\left(\dfrac{13}{2}−3\right)}=\sqrt{\dfrac{13}{2} \left(\dfrac{5}{2}\right) \left(\dfrac{1}{2}\right)\left(\dfrac{7}{2}\right)}=\sqrt{\dfrac{455}{16}} \approx 28 \text{ ft}^2 \end{aligned}\)
- Caroline quiere medir la altura de una torre de radio. Desde cierta distancia de la torre, el ángulo de elevación desde su punto hasta la cima de la torre es\(65^{\circ} \). Caroline camina 100 m más lejos de la torre y mide el ángulo de elevación hasta la cima de la torre a ser\(48^{\circ} \). ¿Qué tan alta es la torre?
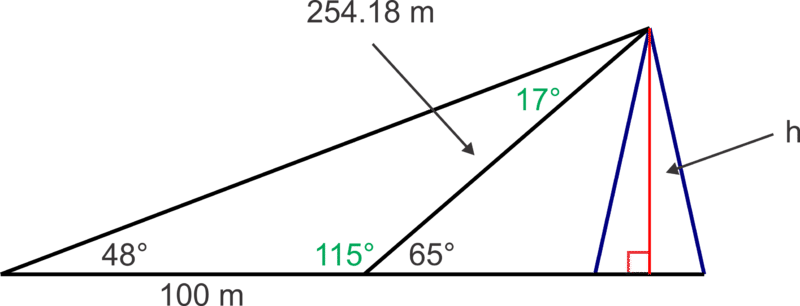
Primero, haz un diagrama para ilustrar la situación.
Podemos usar propiedades de ángulo (par lineal y suma de triángulos) para encontrar los ángulos mostrados en verde en el diagrama.
\(180^{\circ} −65^{\circ} =115^{\circ} \)y\(180^{\circ} −48^{\circ} −115^{\circ} =17^{\circ}\)
A continuación, podemos usar la Ley de Sinos en el triángulo obtuso para encontrar la hipotenusa en el triángulo rectángulo:
\(\begin{aligned} \dfrac{\sin 17^{\circ} }{100} =\dfrac{\sin 48^{\circ} }{x} \\ x=\dfrac{100 \sin 48^{\circ}}{ \sin 17^{\circ} } \approx 254.18 \end{aligned}\)
Finalmente podemos usar la relación sinusoidal en el triángulo rectángulo para encontrar la altura de la torre:
\(\sin 65^{\circ} =\dfrac{h}{254.18}\),\(h=254.18\sin 65^{\circ} \approx 230.37 \text{ m}\)
Anteriormente, se le pidió que encontrara el área del triángulo con lados de longitud 2 pulgadas, 5 pulgadas y 6 pulgadas.
Solución
Primero, encuentra el semiperímetro o s:\(s=\dfrac{1}{2}(2+5+6)=6.5\). A continuación, sustituya nuestros valores por la fórmula de Heron y evalúe:
\(A=\sqrt{6.5(6.5−2)(6.5−5)(6.5−6)}=\sqrt{6.5(4.5)(1.5)(0.5)}=\sqrt{21.94} \approx 4.7 \text{ in.}^2\)
Utilice la regla o fórmula más adecuada (Ley de los senos, Ley de cosenos, fórmula de área con seno o fórmula de Garza) para responder a las siguientes preguntas.
Encuentra el área de un triángulo con longitudes laterales de 50 m, 45 m y 25 m.
Solución
Fórmula de Heron:
\(s=\dfrac{1}{2} (50+45+25)=60\),\(A=\sqrt{60(60−50)(60−45)(60−25)} \approx 561 \text{ m}^2\).
Matthew planea fertilizar su pasto. Cada bolsa de fertilizante afirma cubrir 500 pies cuadrados de pasto. Su propiedad de tierra es aproximadamente en forma de triángulo. Mide dos lados de su patio para ser 75 pies y 100 pies y el ángulo entre ellos es\(72^{\circ} \). ¿Cuántas bolsas de fertilizante debe comprar?
Solución
Fórmula de área con seno:\(\dfrac{1}{2} (75)(100)\sin 72^{\circ} \approx 3566 \text{ ft }^2\), Número de bolsas\(\dfrac{3566}{500} \approx 7.132\approx 8 \text{ bags}\). Redondeamos porque 7 bolsas no es suficiente.
Un par de lados adyacentes en un paralelogramo son 3 pulgadas y 7 pulgadas y el ángulo entre ellos es\(62^{\circ} \), encontrar la longitud de las diagonales.
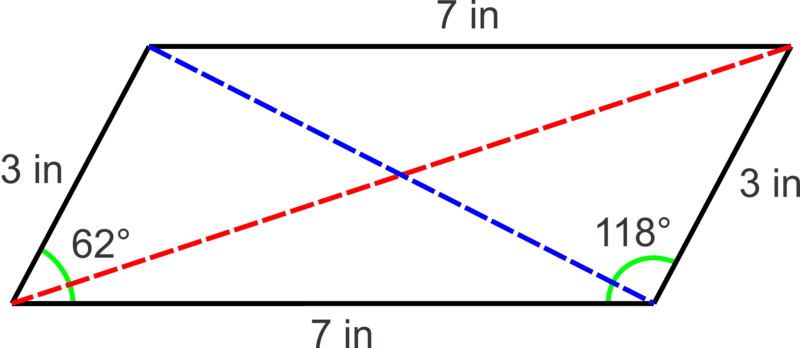
Solución
Ley de Cosinos para encontrar la diagonal azul:
\(\begin{aligned} c^2&=3^2+7^2−2(3)(7)\cos 62^{\circ} \\ c&=\sqrt{38.28}\approx 6.19 \end{aligned}\)
Entonces, 6.19 en
Para encontrar la diagonal verde podemos utilizar la Ley de Cosinos con el ángulo adyacente\(180^{\circ} −62^{\circ} −118^{\circ} \):
\(\begin{aligned} c^2 &=7^2+3^2−2(7)(3)\cos 118^{\circ} \\ c&=\sqrt{77.72} \approx 8.82 \end{aligned}\)
Entonces, 8.82 en
Revisar
Utilice la Ley de los Sinos, la Ley del Coseno, el área de triángulo con seno o la Fórmula de Garza para resolver los problemas de aplicación del mundo real.
- Dos observadores, Rachel y Luis, están parados en la orilla, a 0.5 millas de distancia. Cada uno mide el ángulo entre la costa y un velero en el agua al mismo tiempo. Si el ángulo de Rachel es\(63^{\circ} \) y el ángulo de Luis es\(56^{\circ} \), encuentra la distancia entre Luis y el velero a la centésima de milla más cercana.
- Dos peatones caminan desde extremos opuestos de una cuadra de la ciudad hasta un punto del otro lado de la calle. El ángulo formado por sus caminos es\(125^{\circ} \). Un peatón camina 300 pies y el otro camina 320 pies. ¿Cuánto dura la cuadra de la ciudad al pie más cercano?
- Dos lados y el ángulo incluido de un paralelogramo tienen medidas 3.2 cm, 4.8 cm y\(54.3^{\circ} \) respectivamente. Encuentra las longitudes de las diagonales al décimo de centímetro más cercano.
- Un puente está soportado por tirantes triangulares. Si los lados de cada corsé tienen longitudes de 63 pies, 46 pies y 40 pies, encuentre la medida del ángulo más grande al grado más cercano.
- Encuentra el área triangular, al metro cuadrado más cercano, encerrada por tres piezas de cercado de 123 m, 150 m y 155 m de largo.
- Encuentra el área, a la pulgada cuadrada más cercana, de un paralelogramo con lados de longitud 12 en y 15 pulgadas y ángulo incluido de\(78^{\circ} \).
- Una persona en el punto\(A\) mira hacia el este y ve un OVNI con un ángulo de elevación de\(40^{\circ} \). Al mismo tiempo, otra persona, 1 mi al oeste de A mira hacia el este y mira el mismo OVNI con un ángulo de elevación de\(25^{\circ} \). Encuentra la distancia entre A y el OVNI. ¿Qué tan lejos está el OVNI sobre el suelo? Dar respuestas a la centésima de milla más cercana.
- Encuentra el área de un patio triangular, al metro cuadrado más cercano, con lados de longitud 10 m, 15 m y 16 m.
- Un patio está delimitado en dos lados con cercas de longitud 80 pies y 60 pies. Si estas vallas se encuentran en\(75^{\circ} \) ángulo, ¿cuántos pies de esgrima se requieren para encerrar completamente una región triangular?
- Cuando un niño se para en la orilla de un río y mira a la otra orilla, el ángulo de depresión es\(12^{\circ} \). Si sube a la cima de un árbol de 10 pies y mira a otra orilla, el ángulo de depresión es\(15^{\circ} \). ¿Cuál es la distancia desde la primera posición del niño hasta la otra orilla del río? ¿Qué tan ancho es el río? Da tus respuestas al pie más cercano.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 13.17.

