5.1.4: Transformaciones de Gráficas Polares

Última actualización
Guardar como PDF

Page ID: 107773

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Alteración de la gráfica basada en constantes cambiantes y/o función de una ecuación polar.

Mientras juegas un día con tu calculadora, creas una trama polar que se ve así.

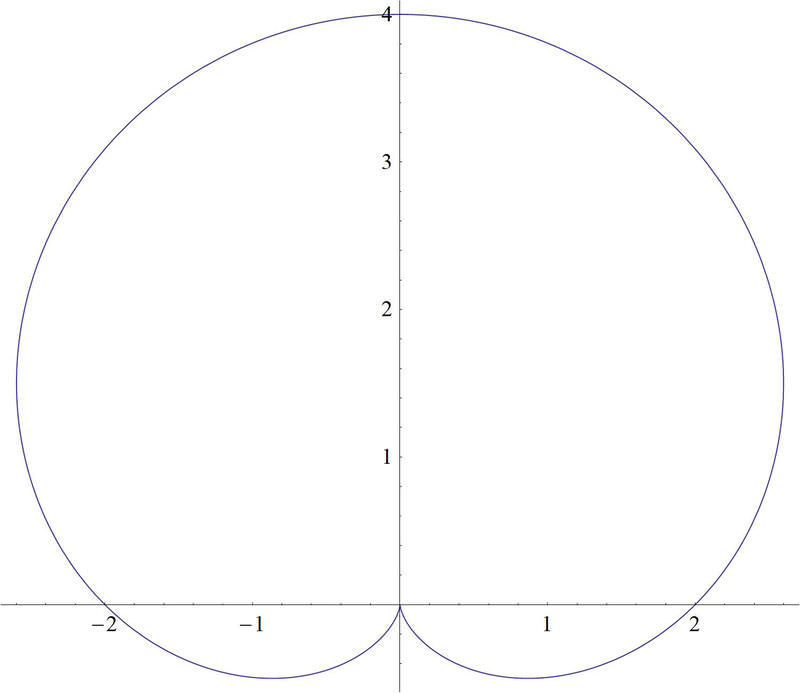
F-d_dc4a5ceb394e733eca36f53c8b49bd89e2975c43cead21a054a301ec+image_tiny+image_tiny.jpg — Figura\(\PageIndex{1}\)

Tu profesor te dice que esta es una trama polar con una ecuación\(2+2\sin \theta \). Tú decides que te gustaría rotar la gráfica, para que en realidad esté de su lado, así

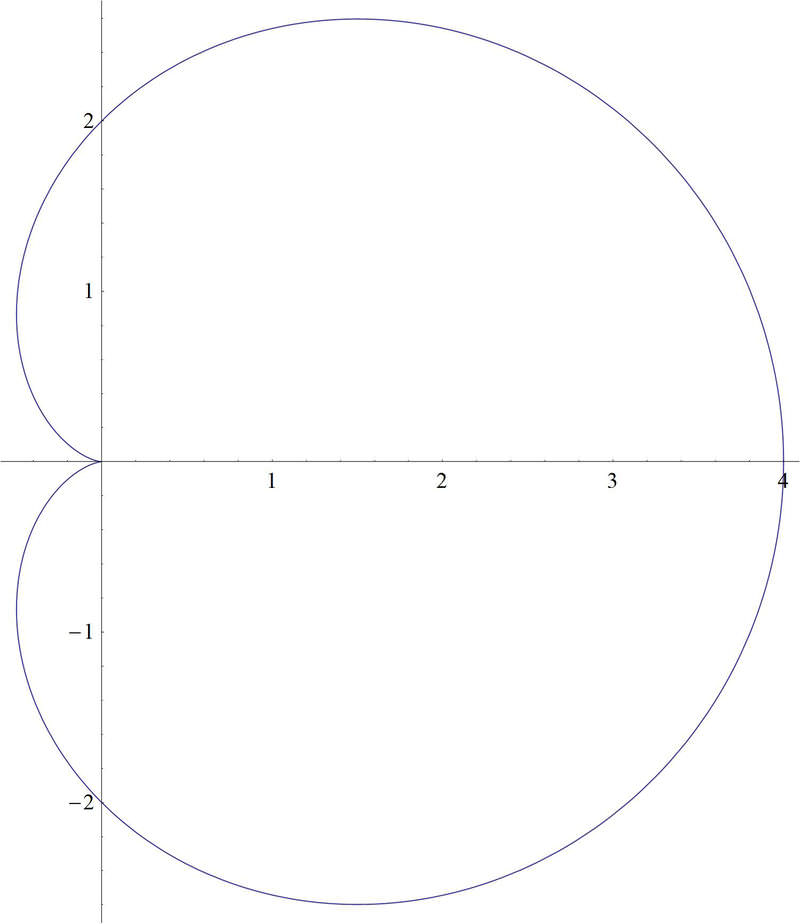
f-d_c8120d9a0f90140222548453602e718349ff037c4dfdcf36990744d2+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

Transformación de gráficos polares

Al igual que en la gráfica en una cuadrícula rectangular, también puedes graficar ecuaciones polares en una cuadrícula polar.

Estas ecuaciones pueden ser simples o complejas. Para comenzar, debes probar algo sencillo como\(r=k\) o\(\theta =k\) donde\(k\) es una constante. La solución para\(r=1.5\) es simplemente todos los pares ordenados tal que\(r=1.5\) y\(\theta \) es cualquier número real. Lo mismo es cierto para la solución de\(\theta =30^{\circ} \). Los pares ordenados serán cualquier número real para\(r\) e\(\theta \) igualarán\(30^{\circ} \). Aquí están las gráficas para cada una de estas ecuaciones polares.

Gráfica de ecuaciones

1. En un plano polar, grafica la ecuación\(r=1.5\)

La solución es todos los pares ordenados de\((r,\theta )\) tal que siempre\(r\) es 1.5. Esto quiere decir que no importa lo que\(\theta \) sea, por lo que la gráfica es un círculo con radio 1.5 y centrado en el origen.

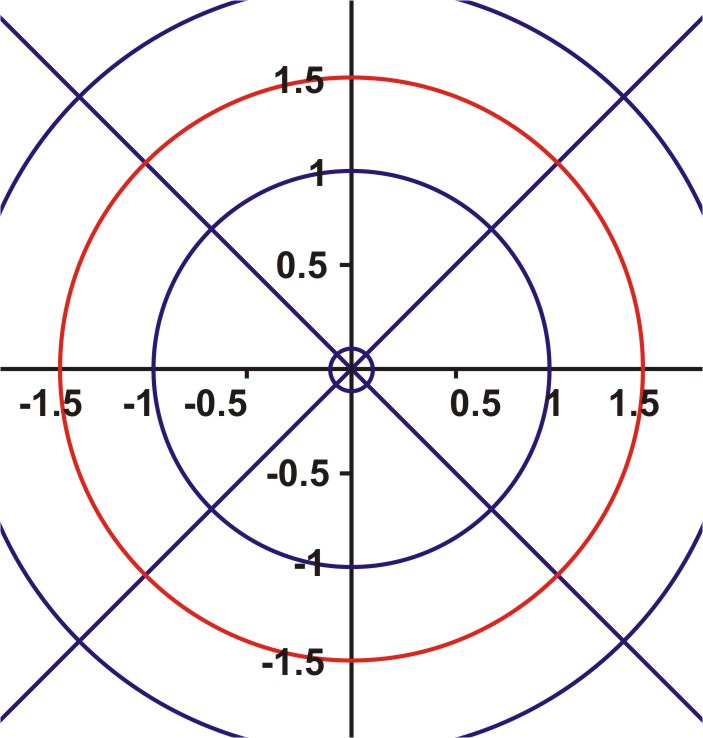
f-d_1fdb2aa94fbffc4a50606772b5a48f4539385c208edcd99f5dbace50+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

2. En un plano polar, grafica la ecuación\(\theta =30^{\circ}\)

Para este problema, el\(r\) valor, o radio, es arbitrario. \(\theta \)debe ser igual\(30^{\circ} \), por lo que el resultado es una línea recta, con un ángulo de elevación de\(30^{\circ} \).

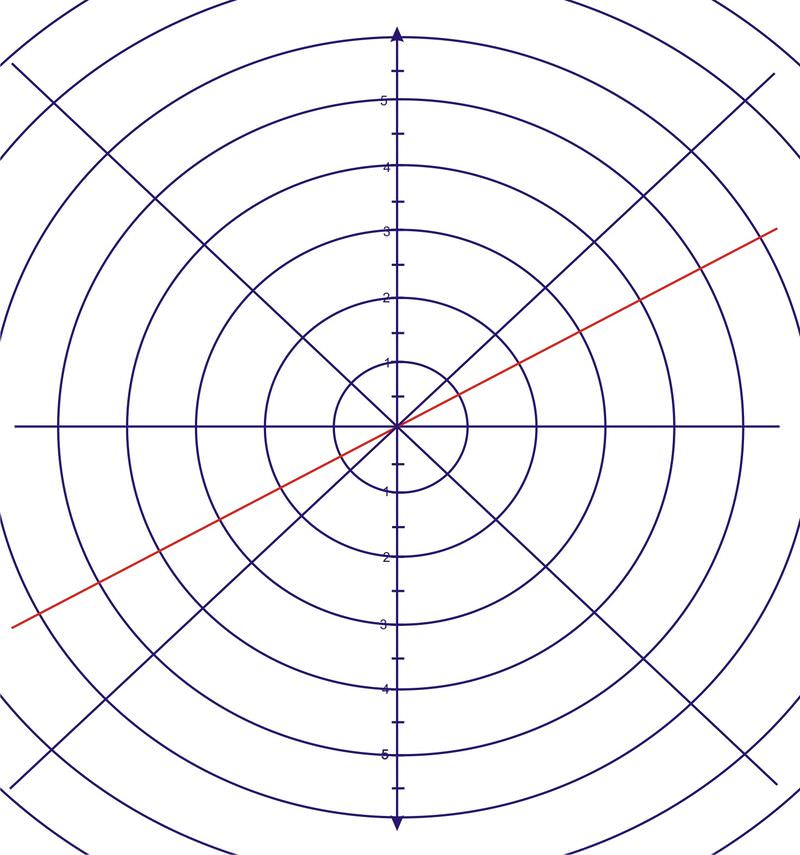
F-d_1a4440a88a74461bcdf347835c7bcf4f3403f808f6a47cfda15cd302+image_tiny+image_tiny.jpg — Figura\(\PageIndex{4}\)

Para comenzar a graficar ecuaciones polares más complicadas, haremos una tabla de valores para\(y=\sin \theta \) o en este caso\(r=\sin \theta \). Una vez completada la tabla, la gráfica se dibujará en un plano polar utilizando las coordenadas\((r,\theta )\).

3. Grafica las siguientes ecuaciones polares en la misma cuadrícula polar y compara las gráficas.

\ (\ begin {array} {ll}
r=5+5\ sin\ theta & r=5-5\ sin\ theta\\
r=5 (1+\ sin\ theta) & r=5 (1-\ sin\ theta)
\ end {array}\)

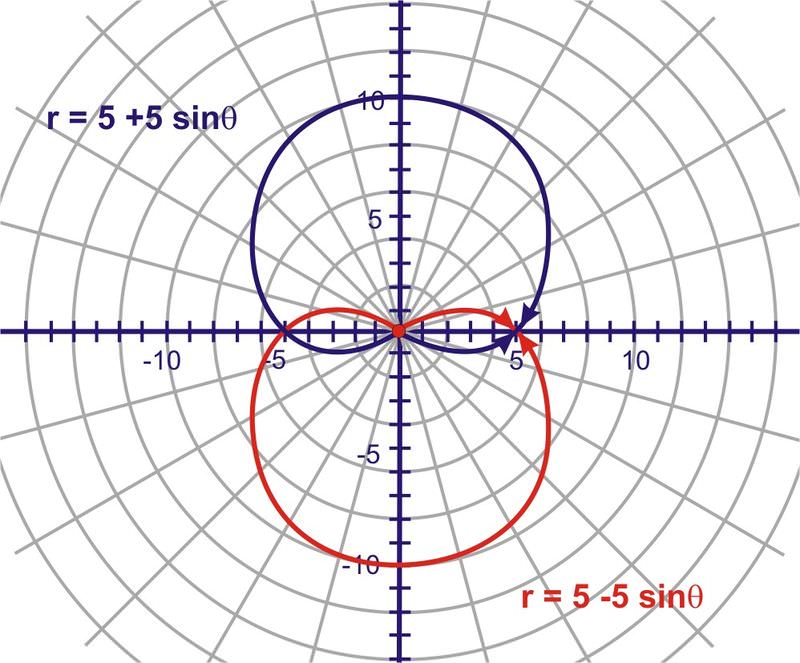
f-d_737a51753aa0b750823f853b0f3f33f416f1aa3c29bcfcecc97661db+image_tiny+image_tiny.jpg — Figura\(\PageIndex{5}\)

El cardioide es simétrico alrededor del\(y\) eje positivo y el punto de indentación está en el polo. El resultado de cambiar + a - es una reflexión en el\(x\) eje −. El cardioide es simétrico alrededor del\(y\) eje negativo y el punto de indentación está en el polo.

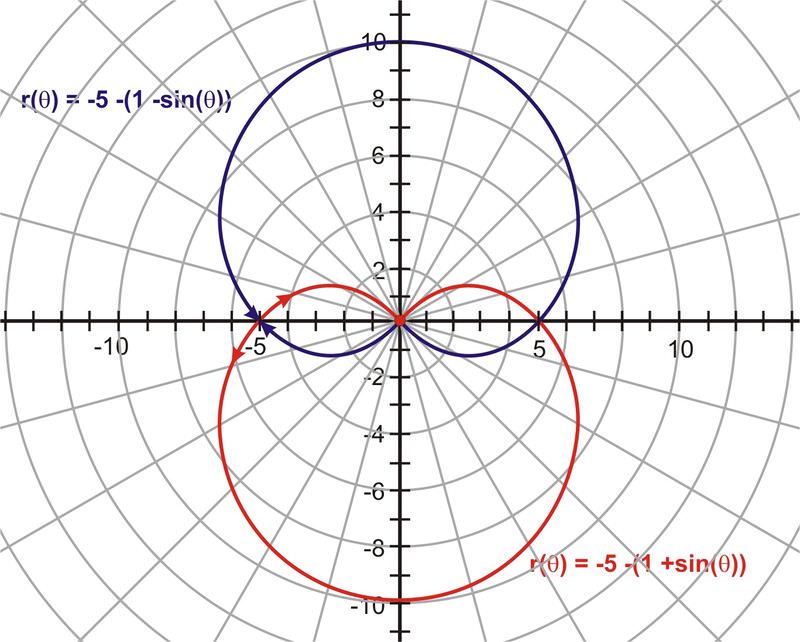
F-d_f40a844e9d6c2160eb580185d3575c9132ef7d856f3954eed4e31cb5+image_tiny+image_tiny.jpg

Cambiar el valor de “\(a\)′′ a un negativo no cambió la gráfica del cardioide.

También es posible crear una curva sinusoidal llamada limaçon. Tiene\(r=a\pm b\sin \theta \) o\(r=a\pm b\cos \theta \) como su ecuación polar. No todos los limaçons tienen el bucle interno como parte de la forma. Algunos pueden curvarse a un punto, tener una sangría simple (conocida como hoyuelo) o curvarse hacia afuera. La forma del limaçon depende de la relación de ab donde a es una constante y b es el coeficiente de la función trigonométrica.

Como hemos visto con los cardioides, es posible crear transformaciones de gráficas de limaçons cambiando valores de constantes en la ecuación de la forma.

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió que graficara una ecuación polar.

Solución

Como has visto en esta sección, las transformaciones a la gráfica de un cardioide se pueden lograr de 2 maneras diferentes. En este caso, se desea rotar la gráfica para que esté alrededor del eje "\(x\)" en lugar del eje\(y\) "”. Para lograr esto, cambia la función de una función sinusoidal a una función coseno:

\(r=2+2\cos \theta\)

Ejemplo\(\PageIndex{2}\)

Grafica la curva\(r=−3−3\cos \theta\)

Solución

\(r=−3−3\cos \theta \).

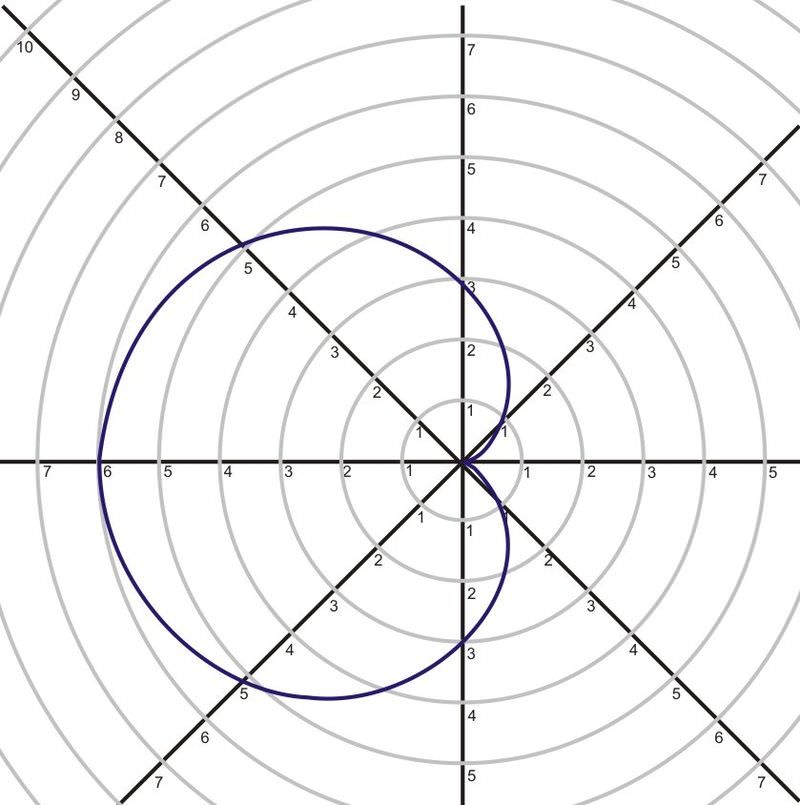
f-d_449a39fc4a1472dd86cbcfa66eec146a0d050fc5f5713ef813d4d672+image_tiny+image_tiny.jpg — Figura\(\PageIndex{7}\)

Ejemplo\(\PageIndex{3}\)

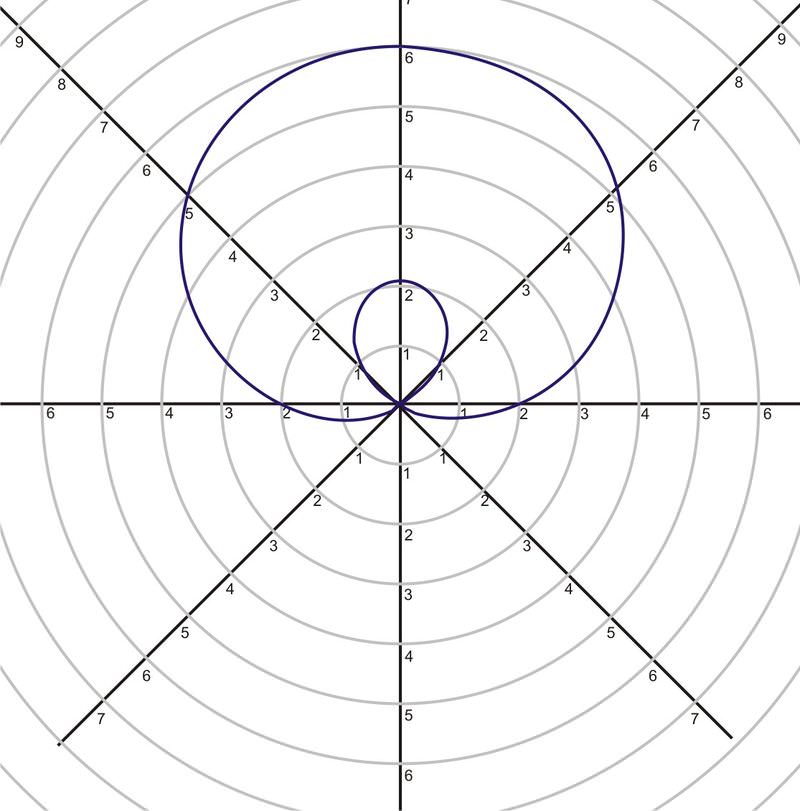
Grafica la curva\(r=2+4\sin \theta\)

Solución

\(r=2+4\sin \theta\)

f-d_dab84ad5cd19681fb98b869e979ffed660d7d1df732da6414301dc3b+image_tiny+image_tiny.jpg — Figura\(\PageIndex{8}\)

Ejemplo\(\PageIndex{4}\)

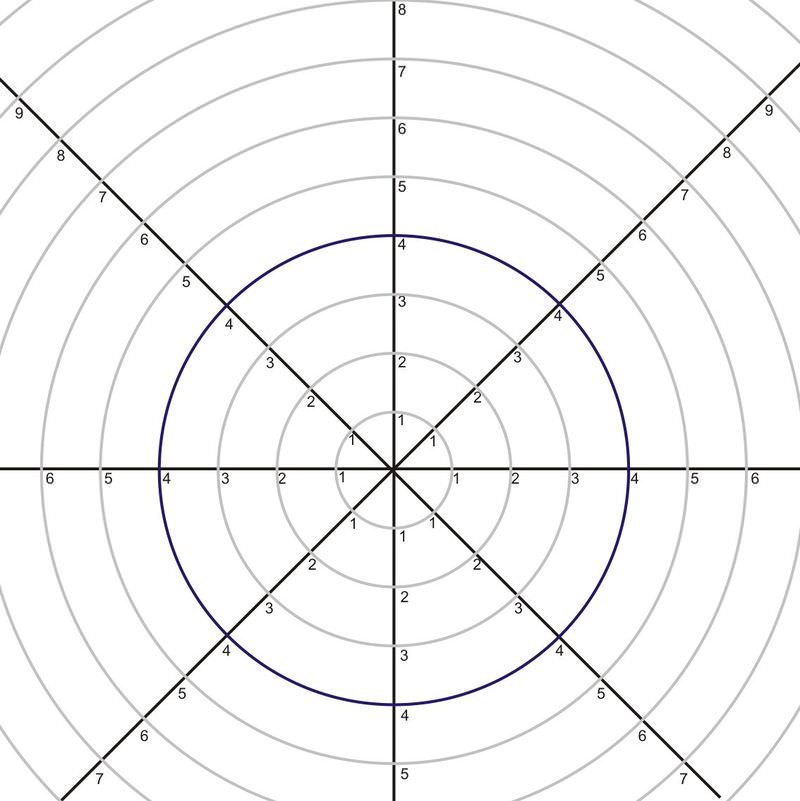
Grafica la curva\(r=4\).

Solución

\(r=4\)

F-d_fd8e15f13df94803ba3215418f99c9fa62bf29428cba0849ed6cac34+image_tiny+image_tiny.jpg — Figura\(\PageIndex{9}\)

Revisar

Grafica cada ecuación.

\(r=4\)
\(\theta =60^{\circ}\)
\(r=2\)
\(\theta =110^{\circ}\)

Grafica cada función usando tu calculadora y bosquejo en tu papel.

\(r=3+3\sin (\theta )\)
\(r=2+4\sin (\theta )\)
\(r=1−5\sin (\theta )\)
\(r=2−2\sin (\theta )\)
\(r=3+6\sin (\theta )\)
\(r=−3+6\sin (\theta )\)
Analizar las conexiones entre las ecuaciones y sus gráficas anteriores. Hacer una hipótesis sobre cómo graficar\(r=a+b\sin (\theta )\) valores positivos o negativos de\(a\) y\(b\) dónde\(b\geq a\).

Grafica cada función usando tu calculadora y bosquejo en tu papel.

\(r=3+3\cos (\theta )\)
\(r=2+4\cos (\theta )\)
\(r=1−5\cos (\theta )\)
\(r=2−2\cos (\theta )\)
\(r=3+6\cos (\theta )\)
\(r=−3+6\cos (\theta )\)
Analizar las conexiones entre las ecuaciones y sus gráficas anteriores. Hacer una hipótesis sobre cómo graficar\(r=a+b\cos (\theta )\) valores positivos o negativos de\(a\) y\(b\) dónde\(b\geq a\).