5.3.9: Forma polar de un número complejo
- Page ID
- 107752
Conversión de\(a + bi\) a\((a, b)\),\((r, theta)\), y\(r\; cis \;theta\).
Los números complejos se pueden graficar en un gráfico polar al igual que los números reales. Descubrirás durante esta lección que en realidad hay algunas formas diferentes de hacerlo.
Se ha aprendido que las gráficas rectangulares se pueden poner en forma polar, y que los puntos en coordenadas rectangulares se pueden trazar en el sistema de coordenadas polares. En esta sección aprenderás a hacer el mismo proceso con números complejos.
Hay tres formas comunes de números complejos que verás al graficar:
- En la forma estándar de:\(z = a + bi\), un número complejo z se puede graficar usando coordenadas rectangulares\((a, b)\). 'a' representa la coordenada x, mientras que 'b' representa la coordenada\(y \) -.
- La forma polar:\((r,\theta )\) que exploramos en una lección anterior, también se puede utilizar para graficar un número complejo. Recuerda que puedes usar x e y para convertir entre formas rectangulares y polares con:\(r=\sqrt{x^2+y^2}\) y\(\tan \theta_{ref}=\left| \dfrac{y}{x} \right|\). Desafortunadamente, hay un problema con el uso de una conversión de forma rectangular a forma polar como:
\(a+bi\rightarrow (r,\theta )\)
o
\(−1−i\sqrt{3}\rightarrow \left(2,\dfrac{4\pi }{3}\right)\)
El problema es que hemos perdido el\(i\). Entonces, para “hacer un seguimiento” de la parte imaginaria, podemos usar otra forma.
- La tercera forma es la forma trigonométrica. A menudo se abrevia como\(r\; cis \;\theta \), abreviatura de:\(z = r(\cos \theta + i\sin \theta )\), y se utilizará con bastante frecuencia a medida que avance. Esta forma proviene de las sustituciones:\(x = r \cos \theta \) y\(y = r \sin \theta \).
usando este hecho, y valores de muestra de 2\(\dfrac{\pi }{3}\) para\(r\) y para\(\theta \), podemos escribir
\(z=−1−i\sqrt{3}=2 \cos \dfrac{4 \pi }{3}+2 i \sin \dfrac{4 \pi }{3}\)
Por último, factorizando el 2, obtenemos:\(z=2 \left(\cos \dfrac{4 \pi }{3}+i \sin \dfrac{4 \pi }{3}\right)\)
Resumen de Formularios
El número complejo:\(z=−1−\sqrt{3}i\), el punto rectangular\((−1,−\sqrt{3})\), el punto polar:\(\left(2,\dfrac{4 \pi }{3}\right)\), y\(2\left(\cos \dfrac{4 \pi }{3}+i \sin \dfrac{4 \pi }{3}\right)\) o\(2 \; cis \; \left(\dfrac{4 \pi }{3}\right)\) todos representan el mismo número.
Pasos para la conversión
Para convertir de forma polar a rectangular, la distancia que el punto (2, 2) está desde el origen se puede encontrar por
\(d=\sqrt{x^2+y^2} \text{ or } \sqrt{2^2+2^2} \qquad d=\sqrt{8} \text{ or } 2\sqrt{2}\)
El ángulo de referencia (es decir, el ángulo correspondiente en el primer cuadrante) que el segmento de línea entre el punto y el origen se puede encontrar por
\(\tan \theta_{ref}=\left| \dfrac{y}{x} \right|\)
para\(z = 2 + 2i\),
\(\begin{aligned} \tan \theta_{ref}=22 \\ \tan \theta_{ref}=1\end{aligned}\)
Dado que este punto está en el primer cuadrante (tanto la coordenada x como y son positivas) el ángulo debe ser\(45^{\circ}\) o\(\dfrac{\pi }{4}\) radianes.
También es posible que cuando\(\tan \theta = 1\) el ángulo pueda estar en el tercer cuadrante o 5\ pi 4 radianes. Pero este ángulo no va a satisfacer las condiciones del problema, ya que un ángulo de tercer cuadrante debe tener tanto x como y como negativos.
Nota: Al usar\(\tan \theta =\dfrac{y}{x}\), primero debe considerar, el cociente\(\left|yx \right|\) y encontrar el primer ángulo de cuadrante que satisfaga esta condición. Este ángulo se llamará el ángulo de referencia, denotado\(\theta_{ref}\). Encuentra el ángulo real analizando a qué cuadrante se le deben dar los signos x e y al ángulo.
El número complejo\(2 + 2i\) o (2, 2) en forma rectangular tiene coordenadas polares\(\left(2\sqrt{2}, \dfrac{\pi }{4}\right)\)
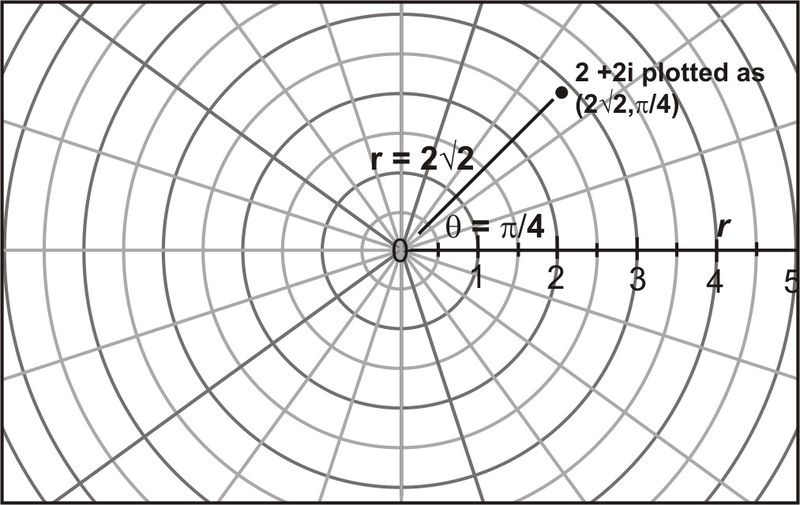
Gráfica en forma polar:\(z=−1−i\sqrt{3}\).
Solución
Así es como se ve en el sistema de coordenadas rectangulares:
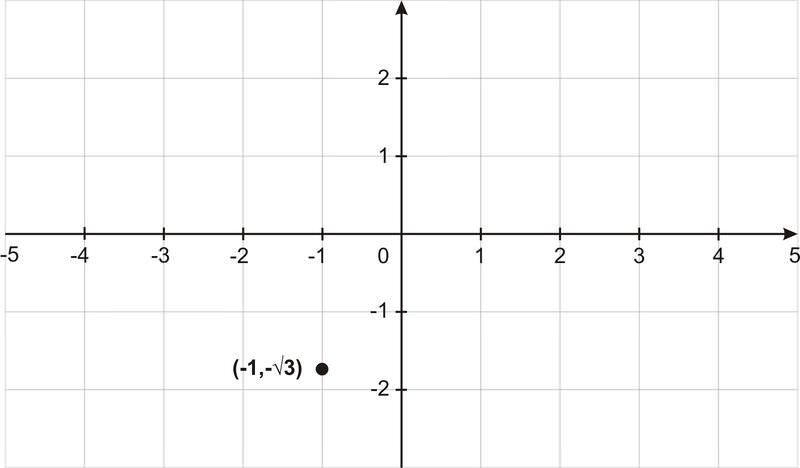
En forma polar, encontramos\(r\) con
\(\begin{aligned} r&=\sqrt{a^2+b^2}\\ &=\sqrt{(−1)^2+(−\sqrt{3})^2}\\ &=\sqrt{1+3}\\\ &=\sqrt{4} \\ &=2 \end{aligned} \)
y para encontrar\(\theta \),
\(\begin{aligned} \tan \theta_{ref}&=\left|\dfrac{−\sqrt{3}}{−1}\right| \\ \tan \theta_{ref}&=\sqrt{3} \\ \theta_{ref}&=tan−1 \sqrt{3}\\ \theta_{ref}&=\dfrac{\pi }{3} \end{aligned}\)
Dado que este ángulo se encuentra en el cuadrante 4º,\(\theta =\dfrac{4 \pi }{3}\).
Encuentra las coordenadas polares que representan el número complejo\(z=3−3\sqrt{3}i\).
Solución
\(a = 3\)y\(b = −3\sqrt{3}\): las coordenadas rectangulares del punto son\((3,−3\sqrt{3})\).
Ahora, dibuja un triángulo rectángulo en forma estándar. Encuentra la distancia que el punto está desde el origen y el ángulo que el segmento de línea que representa esta distancia hace con el eje +x:
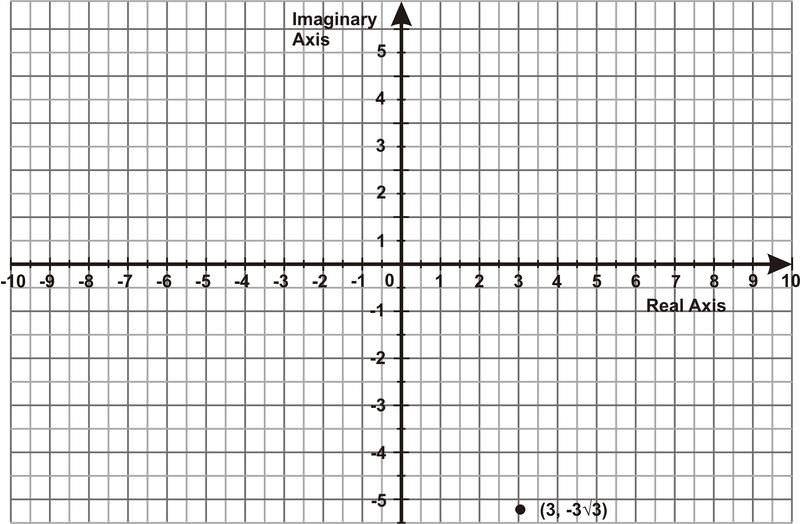
Sabemos\(a = 3\),\(b=−3\sqrt{3}\)
\(\begin{aligned} r&=\sqrt{3^2+(−3\sqrt{3})^2}\\ &=\sqrt{9+27}\\&=\sqrt{36} \\ &=6 \end{aligned}\)
Y para el ángulo,
\(\begin{aligned} \tan \theta_{ref}&=\left|\dfrac{(−3\sqrt{3})}{3}\right| \\ \tan \theta_{ref}&=\sqrt{3} \\ \theta_{ref}&=\dfrac{\pi }{3}\end{aligned}\)
Pero, ya que es un ángulo de 4º cuadrante
\(\theta =\dfrac{5 \pi }{3}\)
El punto rectangular\((3,−3\sqrt{3}i)\) es equivalente al punto polar\(\left(6,5\dfrac{\pi }{3}\right)\).
En\(r\; cis \;\theta\) forma,\((3,−3\sqrt{3}i)\) es\(6\left(\cos \dfrac{5 \pi }{3}+i \sin \dfrac{5 \pi }{3}\right)\).
Convierta los siguientes números complejos en forma polar, use una calculadora gráfica equivalente a TI-84:
- \(\sqrt{3}−i\)
- \(9\sqrt{3}+9i\)
Solución
En el TI-84: vaya a [ANGLE] (o [2nd] función) [APPS]. Desplázate hacia abajo hasta 5 o “R-Pr (“y presiona [Enter]. A continuación, ingresa las coordenadas rectangulares y cierra el paréntesis. Presiona [Enter], aparece el valor “r”. Desplázate hacia abajo hasta 6R-P\ theta y el ángulo polar aparece en forma de radianes decimales.
Nota: También bajo el menú [ÁNGULO], los comandos 7 y 8 permiten la transformación de forma polar a forma rectangular.
Trazar el número complejo\(z=12+9i\).
Solución
- ¿Qué se necesita para trazar este punto en el plano polar?
Primero, necesitaremos saber\(r\) y\(\theta \).
- ¿Cómo podría determinarse el valor r?
El valor r es la hipotenusa de un triángulo con otros dos lados,\(A=12\) y\(B=9\). Se puede determinar con el teorema de Pitágoras:\(A^2+B^2=C^2\).
- ¿Cuál es el\(r\) para este punto?
El\(r\) valor para este punto es\(\sqrt{144+81}\rightarrow \sqrt{225}=15\).
- ¿Cómo\(\theta\) se podría determinar?
\ theta se puede calcular usando cualquiera\(\sin \theta =\dfrac{9}{15}\) o\(\cos \theta =\dfrac{12}{15}\).
- ¿Qué es\(\theta \) para este punto?
Para este punto,\(\sin \theta =\dfrac{3}{5}\rightarrow 37^{\circ}\) o\(\cos \theta =45\rightarrow 37^{\circ}\).
- ¿Cómo\(z=12+9i\) se vería en el plano polar?
\(z=12+9i\)se parece a la imagen de abajo cuando se traza en un plano polar.
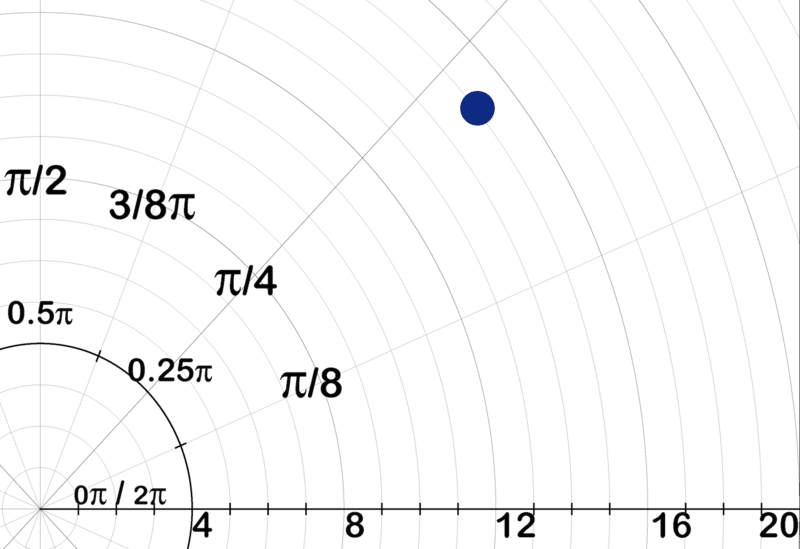
¿En qué cuadrante\(z=−3+2i\) ocurre cuando se grafica?
Solución
El punto\(z=−3+2i\) ocurre 3 unidades a la izquierda y 2 unidades hacia arriba, colocándolo en el Cuadrante II.
¿Cuáles son las coordenadas\(z = -3 + 2i\) en forma polar y trigonométrica?
Solución
Para identificar las coordenadas de\(z=−3+2i\) en forma polar y trigonométrica:
\(\begin{aligned} r&=\sqrt{(−3^2)+(2^2)}\rightarrow \sqrt{13} && \text{First find } r \\ \sin \theta &=2\sqrt{13} \rightarrow 33.7^{\circ} && \text{Second, find }\theta \\ &\therefore [\sqrt{13} ,33.7^{\circ}] && \text{are the coordinates in polar form.} \\ &\therefore r\; cis \;\sqrt{13} \left(\dfrac{\pi}{5}\right) && \text{are the coordinates in } r\; cis \; \text{ form} \end{aligned}\)
¿Cuáles serían las coordenadas polares del punto graficado a continuación?

Solución
Las coordenadas rectangulares son,\((4.5, 3i)\) por lo tanto, el número complejo sería\(z=4.5+3i\)
\(r=5.4\)usando el Teorema de Pitágoras como en Q #3
\(\theta =33.75^{\circ}\)usando\(\sin =\dfrac{\text{opp}}{\text{hyp}}\) como en Q #3
\(\therefore [5.4,33.65^{\circ}]\)es el punto en forma polar\(\therefore r\; cis \;5.4\left(\dfrac{\pi}{5}\right)\) son las coordenadas en\(r\; cis \;\) forma
Revisar
Trazar cada número complejo en el plano complejo. Encuentra su forma polar, [r,\ theta] y dar el argumento\ theta en grados.
- a)\(1+i\) b)\(i\) c)\((1+i)i\)
- a)\(−2\) b)\(3i\) c)\((−2)(3i)\)
- a)\(1+i\) b)\(1−i\) c)\((1+i)(1−i)\)
- a)\(1+i\sqrt{3}\) b)\(\sqrt{3}−i c)(1+i\sqrt{3})(\sqrt{3}−i)\)
- Cuáles son las coordenadas rectangulares para el punto que se grafica a continuación.
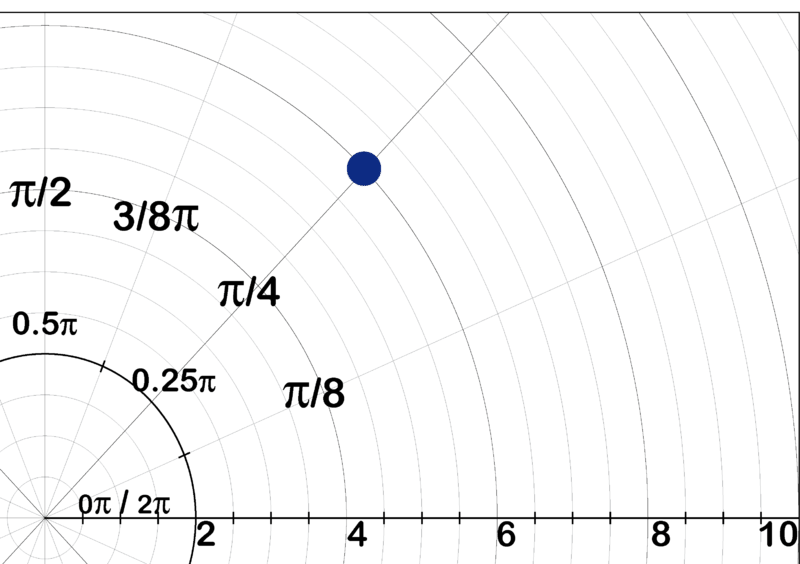
Calcule y convierta a\(r\; cis \;\) forma.
- \(\dfrac{−2−2i}{1−i}\)
- \(1+i^6\)
- \(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i^{10}\)
Cambiar a forma polar.
- \(−3−2i\)
- \(2\sqrt{3}−2i\)
Cambiar a forma rectangular.
- \(15(\cos 120^{\circ}+i\sin 120^{\circ})\)
- \(12\left(\cos \dfrac{\pi }{3}+i\sin \dfrac{\pi }{3}\right)\)
- Para el número complejo en forma estándar\(x+iy\) encontrar: a) Forma polar b) Forma trigonométrica (Pista: Recordemos eso\(x=r\cos \theta \) y\(y=r\sin \theta \))
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.8.
El vocabulario
| Término | Definición |
|---|---|
| \(r\; cis \;\theta\) | \(r\; cis \;\theta \)es la taquigrafía de la expresión\(r\cos \theta +ri\sin \theta \). |
| número complejo | Un número complejo es la suma de un número real y un número imaginario, escritos en la forma a+bi. |
| sistema de coordenadas polares | El sistema de coordenadas polares es un sistema de coordenadas especial en el que la ubicación de cada punto está determinada por su distancia desde el polo y su ángulo con respecto al eje polar. |
| forma polar | La forma polar de un punto o una curva se da en términos de r y\(\theta \) y se grafica en el plano polar. |
| cuadrante | Un cuadrante es un cuarto del plano de coordenadas. Los cuatro cuadrantes se numeran usando los números romanos I, II, III y IV, comenzando en la parte superior derecha y aumentando en sentido antihorario. |
| Ángulo de referencia | Un ángulo de referencia es el ángulo formado entre el lado terminal del ángulo y el más cercano del eje x positivo o negativo. |
| forma trigonométrica | Escribir un número complejo en forma trigonométrica significa escribirlo en el formulario\(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \)es la taquigrafía de esta expresión. |
| forma polar trigonométrica | Escribir un número complejo en forma trigonométrica significa escribirlo en el formulario\(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \)es la taquigrafía de esta expresión. |
Recursos adicionales
Práctica: Forma polar de un número complejo

