5.7: Correlaciones

Hasta este punto nos hemos centrado enteramente en cómo construir estadísticas descriptivas para una sola variable. Lo que no hemos hecho es hablar de cómo describir las relaciones entre variables en los datos. Para ello, queremos hablar mayormente de la correlación entre variables. Pero primero, necesitamos algunos datos.

datos

Después de pasar tanto tiempo mirando los datos de AFL, me estoy empezando a aburrir con los deportes. En cambio, volvamos a un tema cercano al corazón de cada padre: dormir. El siguiente conjunto de datos es ficticio, pero basado en eventos reales. Supongamos que tengo curiosidad por saber cuánto afectan los hábitos de sueño de mi hijo pequeño a mi estado de ánimo. Digamos que puedo calificar mi malhumorado con mucha precisión, en una escala de 0 (para nada gruñón) a 100 (gruñón como un anciano muy, muy gruñón). Y, supongamos también que llevo bastante tiempo midiendo mi malhumordad, mis patrones de sueño y los patrones de sueño de mi hijo. Digamos, por 100 días. Y, siendo un nerd, he guardado los datos como un archivo llamado Parenthood.rdata. Si cargamos los datos...

load( "./data/parenthood.Rdata" )
who(TRUE)

##    -- Name --     -- Class --   -- Size --
##    parenthood     data.frame    100 x 4   
##     $dan.sleep    numeric       100       
##     $baby.sleep   numeric       100       
##     $dan.grump    numeric       100       
##     $day          integer       100

... vemos que el archivo contiene un solo marco de datos llamado parentthood, que contiene cuatro variables dan.sleep, baby.sleep, dan.grump y day. Si echamos un vistazo a los datos usando head () los datos, esto es lo que obtenemos:

head(parenthood,10) 

##    dan.sleep baby.sleep dan.grump day
## 1       7.59      10.18        56   1
## 2       7.91      11.66        60   2
## 3       5.14       7.92        82   3
## 4       7.71       9.61        55   4
## 5       6.68       9.75        67   5
## 6       5.99       5.04        72   6
## 7       8.19      10.45        53   7
## 8       7.19       8.27        60   8
## 9       7.40       6.06        60   9
## 10      6.58       7.09        71  10

A continuación, calcularé algunas estadísticas descriptivas básicas:

describe( parenthood )

##            vars   n  mean    sd median trimmed   mad   min    max range
## dan.sleep     1 100  6.97  1.02   7.03    7.00  1.09  4.84   9.00  4.16
## baby.sleep    2 100  8.05  2.07   7.95    8.05  2.33  3.25  12.07  8.82
## dan.grump     3 100 63.71 10.05  62.00   63.16  9.64 41.00  91.00 50.00
## day           4 100 50.50 29.01  50.50   50.50 37.06  1.00 100.00 99.00
##             skew kurtosis   se
## dan.sleep  -0.29    -0.72 0.10
## baby.sleep -0.02    -0.69 0.21
## dan.grump   0.43    -0.16 1.00
## day         0.00    -1.24 2.90

Finalmente, para dar una representación gráfica de cómo se ve cada una de las tres variables interesantes, la Figura 5.6 traza histogramas.

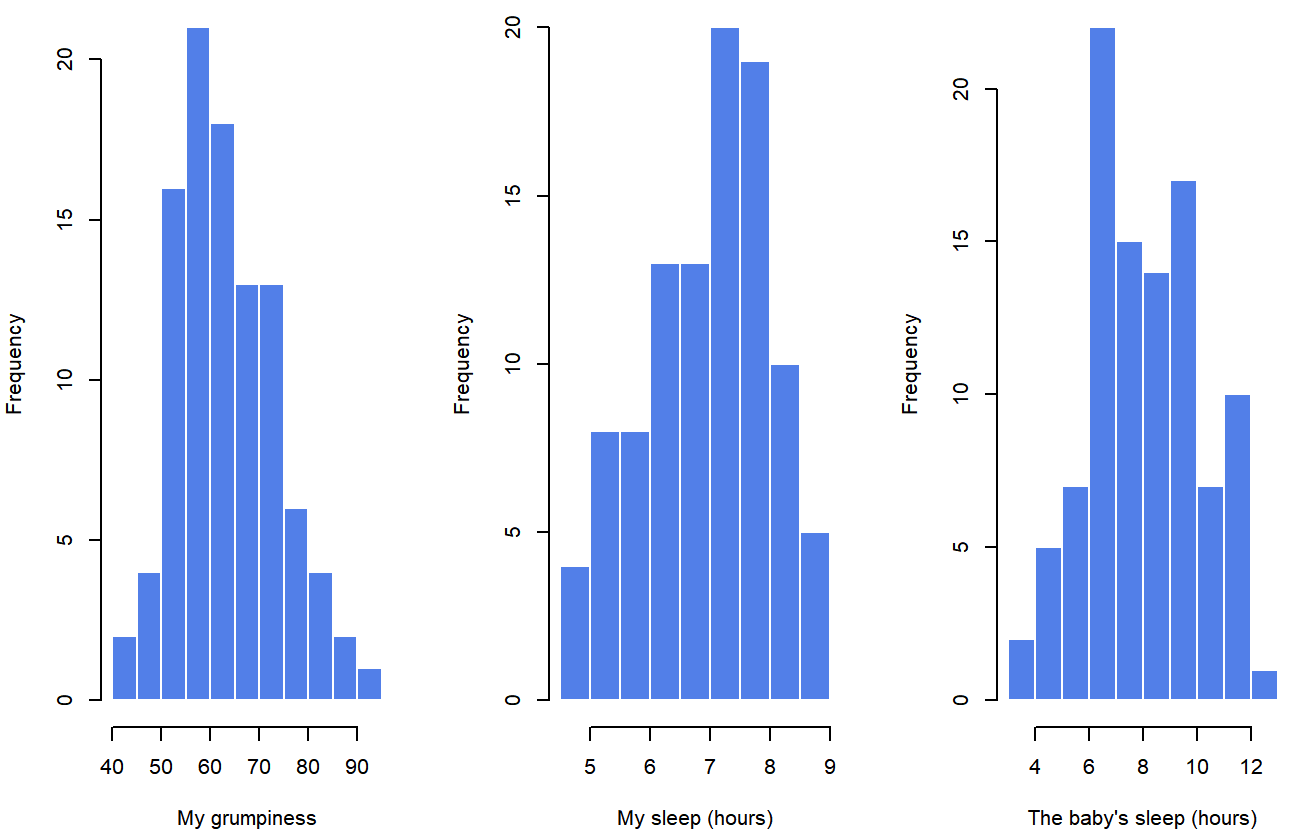
Figura 5.6: Histogramas para las tres variables interesantes en el conjunto de datos de paternidad

Una cosa a tener en cuenta: el hecho de que R pueda calcular docenas de estadísticas diferentes no significa que debas reportarlas todas. Si estuviera redactando esto para un reporte, probablemente escogería esas estadísticas que son de mayor interés para mí (y para mis lectores), y luego las pondría en una mesa bonita y sencilla como la de Table?? . ⁷⁹ Observe que cuando lo puse en una mesa, le di a todo nombres “legibles por humanos”. Esto siempre es una buena práctica. Observe también que no voy a dormir lo suficiente. Esto no es una buena práctica, pero otros padres me dicen que es una práctica estándar.

Cuadro 5.2: Estadística descriptiva de los datos de paternidad.

variable	min	max	media	mediana	std. dev	IQR
La maldad de Dan	41	91	63.71	62	10.05	14
Las horas de Dan durmieron	4.84	9	6.97	7.03	1.02	1.45
Las horas del hijo de Dan durmieron	3.25	12.07	8.05	7.95	2.07	3.21

fuerza y dirección de una relación

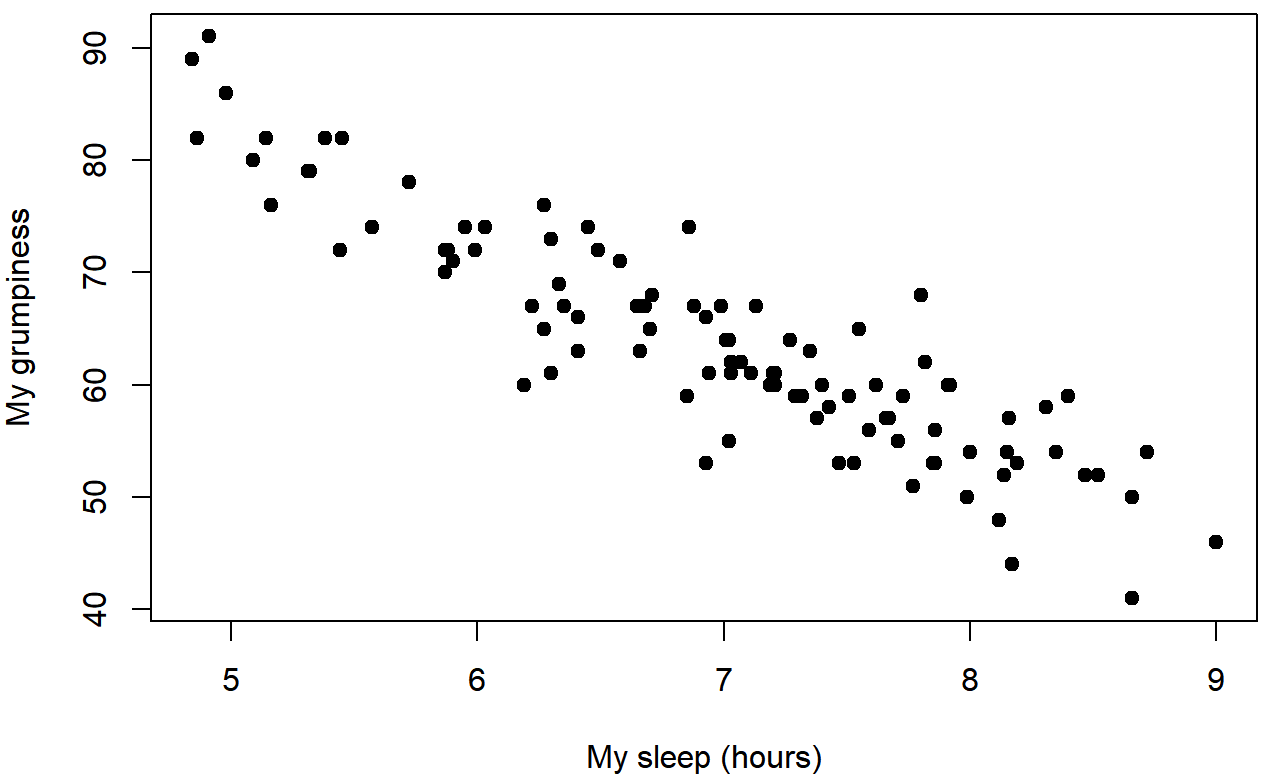
Figura 5.7: Gráfica de dispersión que muestra la relación entre dan.sleep y dan.grump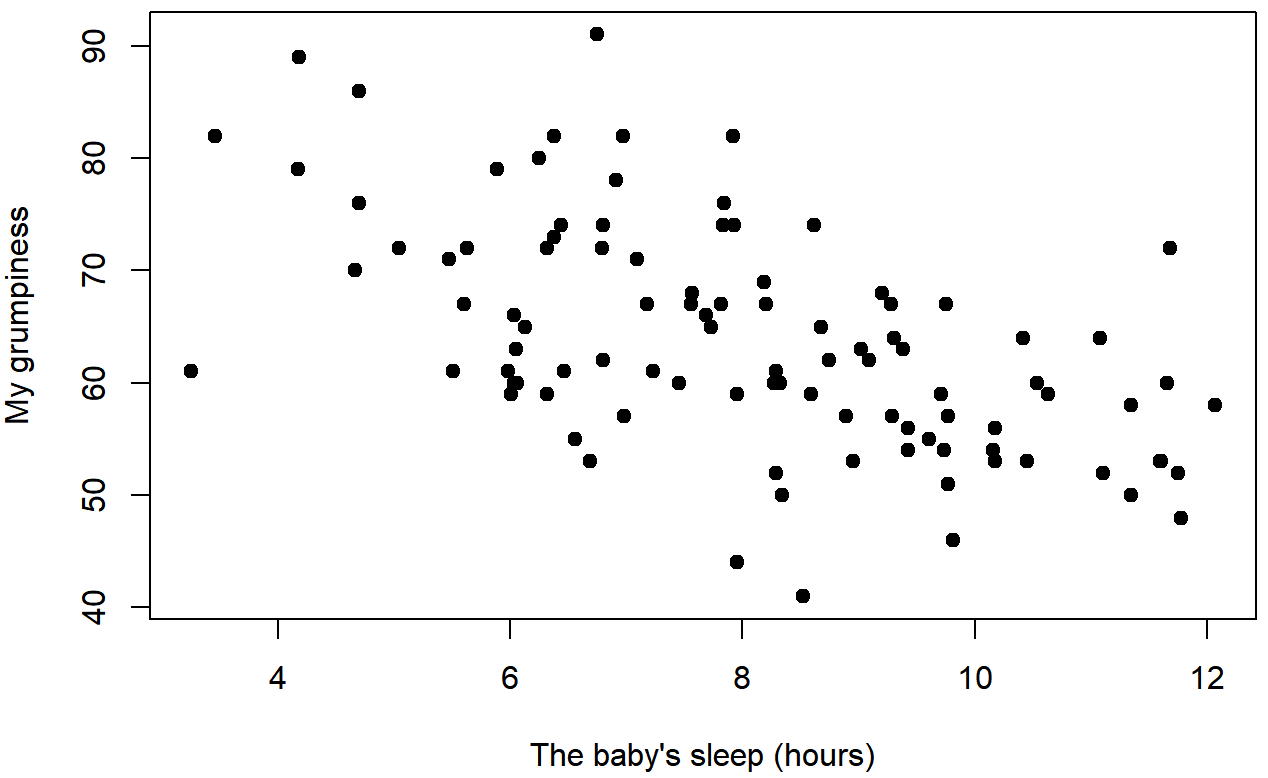

Figura 5.8: Gráfica de dispersión que muestra la relación entre baby.sleep y dan.grump

Podemos dibujar diagramas de dispersión para darnos una idea general de cuán estrechamente relacionadas están dos variables. Sin embargo, lo ideal sería que quisiéramos decir un poco más al respecto que eso. Por ejemplo, comparemos la relación entre dan.sleep y dan.grump (Figura 5.7 con la que existe entre baby.sleep y dan.grump (Figura 5.8. Al mirar estas dos parcelas una al lado de la otra, está claro que la relación es cualitativamente la misma en ambos casos: ¡más sueño equivale a menos gruñón! Sin embargo, también es bastante obvio que la relación entre dan.sleep y dan.grump es más fuerte que la relación entre baby.sleep y dan.grump. El terreno de la izquierda es “más limpio” que el de la derecha. Lo que se siente es que si quieres predecir cuál es mi estado de ánimo, te ayudaría un poco saber cuántas horas durmió mi hijo, pero sería más útil saber cuántas horas dormí.

En contraste, consideremos la Figura 5.8 frente a la Figura 5.9. Si comparamos la gráfica de dispersión de “baby.sleep v dan.grump” con la gráfica de dispersión de “`baby.sleep v dan.sleep”, la fuerza general de la relación es la misma, pero la dirección es diferente. Es decir, si mi hijo duerme más, yo duermo más (relación positiva, pero si duerme más entonces me pongo menos gruñón (relación negativa).

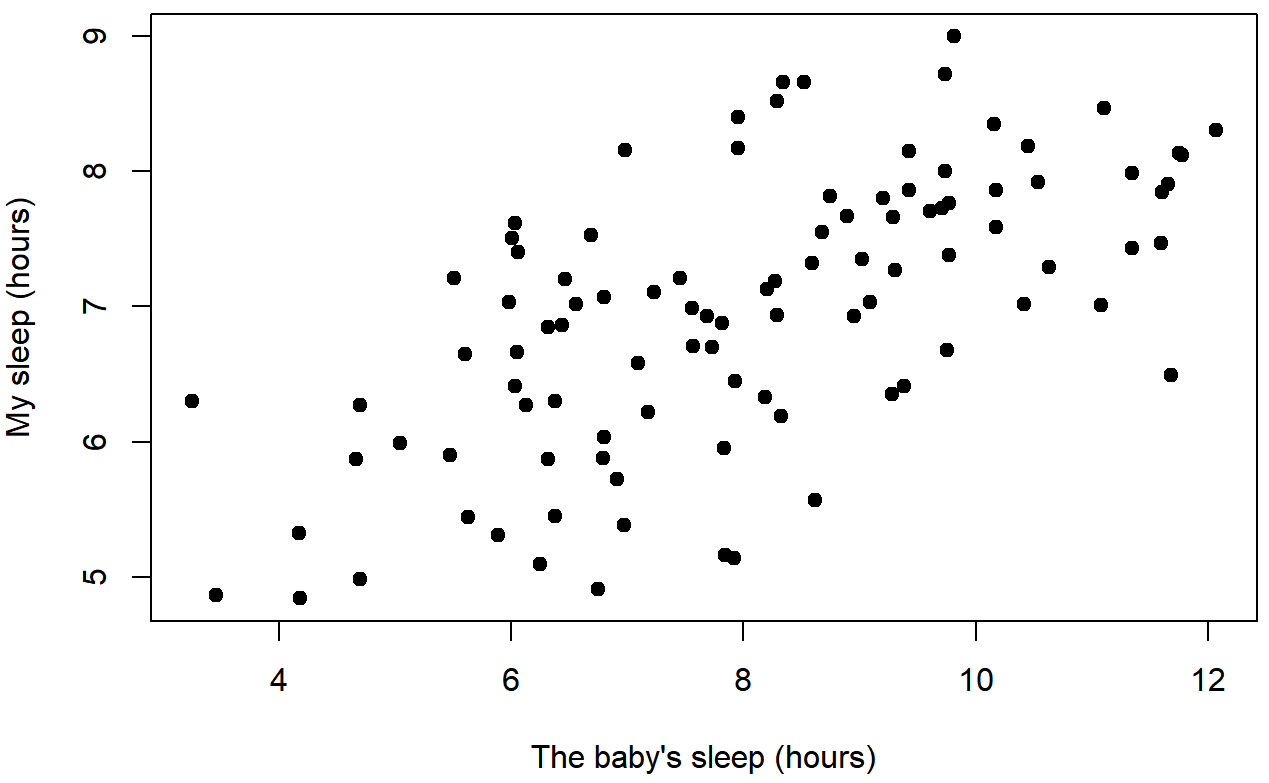
Figura 5.9: Gráfica de dispersión que muestra la relación entre baby.sleep y dan.sleep

coeficiente de correlación

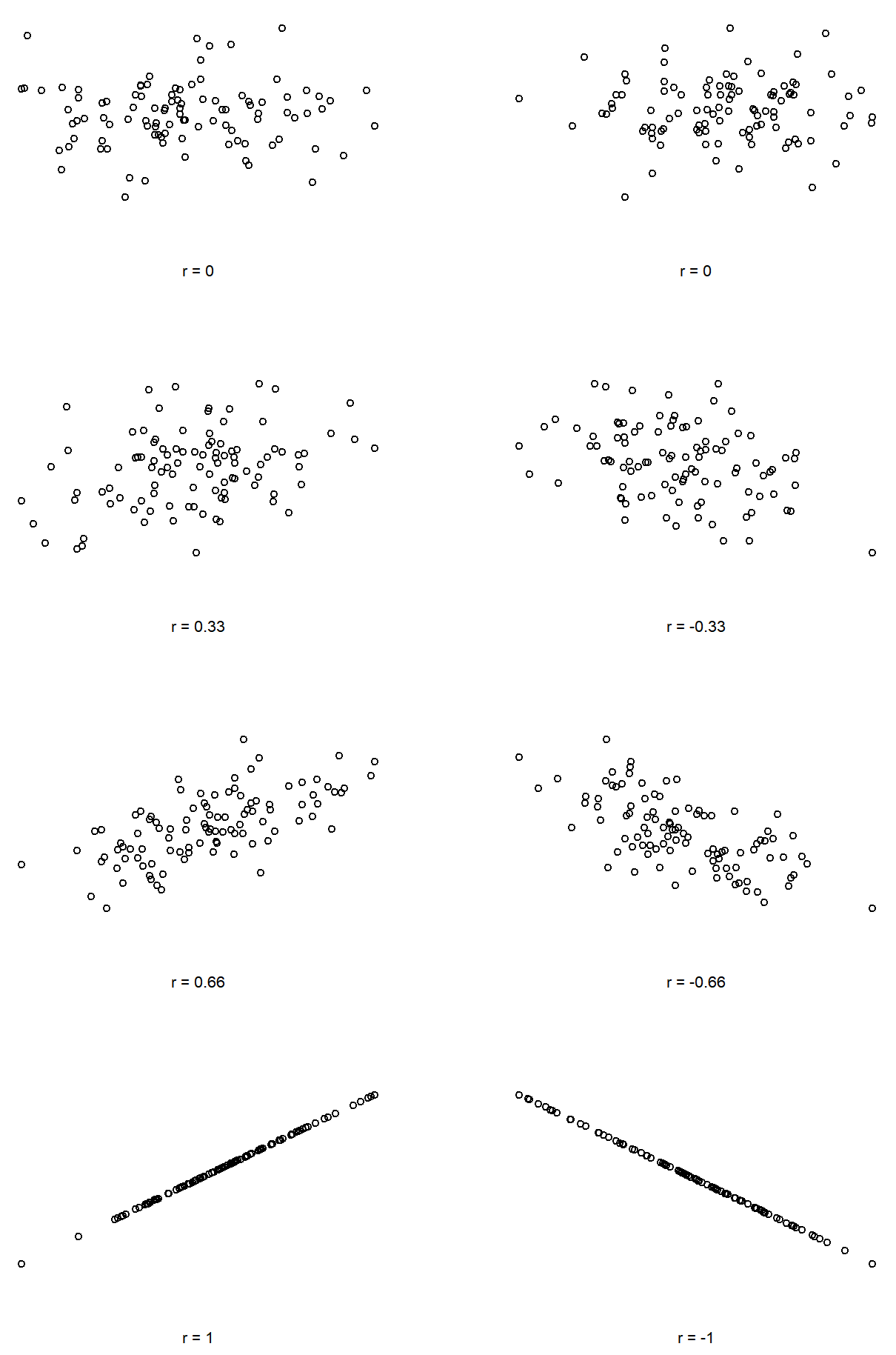
Podemos hacer estas ideas un poco más explícitas introduciendo la idea de un coeficiente de correlación (o, más específicamente, el coeficiente de correlación de Pearson), que tradicionalmente se denota con r. El coeficiente de correlación entre dos variables X e Y (a veces denotado RXy), que definiremos con mayor precisión en la siguiente sección, es una medida que varía de −1 a 1. Cuando r=−1 significa que tenemos una relación negativa perfecta, y cuando r=1 significa que tenemos una relación positiva perfecta. Cuando r=0, no hay ninguna relación en absoluto. Si nos fijamos en la Figura 5.10, puede ver varias gráficas que muestran cómo son las diferentes correlaciones.

Figura 5.10: Ilustración del efecto de variar la fuerza y dirección de una correlación

La fórmula para el coeficiente de correlación de Pearson se puede escribir de varias maneras diferentes. Creo que la forma más sencilla de anotar la fórmula es dividirla en dos pasos. En primer lugar, introduzcamos la idea de una covarianza. La covarianza entre dos variables X e Y es una generalización de la noción de varianza; es una forma matemáticamente sencilla de describir la relación entre dos variables que no es terriblemente informativa para los humanos:

\ [
\ nombreoperador {Cov} (X, Y) =\ dfrac {1} {N-1}\ suma_ {i=1} ^ {N}\ izquierda (X_ {i} -\ bar {X}\ derecha)\ izquierda (Y_ {i} -\ bar {Y}\ derecha)
\ nonumber\]

Porque estamos multiplicando (es decir, tomando el “producto” de) una cantidad que depende de X por una cantidad que depende de Y y luego promediando ⁸⁰, se puede pensar en la fórmula para la covarianza como un “producto cruzado promedio” entre X e Y. La covarianza tiene la propiedad agradable que, si X e Y son completamente sin relación, entonces la covarianza es exactamente cero. Si la relación entre ellos es positiva (en el sentido mostrado en la Figura @reffig:corr) entonces la covarianza también es positiva; y si la relación es negativa entonces la covarianza también es negativa. En otras palabras, la covarianza captura la idea cualitativa básica de correlación. Desafortunadamente, la magnitud bruta de la covarianza no es fácil de interpretar: depende de las unidades en las que se expresen X e Y, y peor aún, las unidades reales en las que se expresa la covarianza en sí son realmente raras. Por ejemplo, si X se refiere a la variable dan.sleep (unidades: horas) e Y se refiere a la variable dan.grump (unidades: gruñones), entonces las unidades para su covarianza son “horas × gruñones”. Y no tengo ni idea de lo que eso significaría.

El coeficiente de correlación de Pearson r soluciona este problema de interpretación estandarizando la covarianza, prácticamente de la misma manera que la puntuación z estandariza una puntuación bruta: dividiendo por la desviación estándar. Sin embargo, debido a que tenemos dos variables que contribuyen a la covarianza, la estandarización solo funciona si dividimos por ambas desviaciones estándar. ⁸¹ En otras palabras, la correlación entre X e Y puede escribirse de la siguiente manera:

\ [
r_ {X Y} =\ dfrac {\ nombreoperador {Cov} (X, Y)} {\ hat {\ sigma} _ {X}\ hat {\ sigma} _ {Y}}
\ nonumber\]

Al hacer esta estandarización, no solo mantenemos todas las buenas propiedades de la covarianza discutida anteriormente, sino que los valores reales de r están en una escala significativa: r=1 implica una relación positiva perfecta, y r=−1 implica una relación negativa perfecta. Voy a ampliar un poco más sobre este punto más adelante, en la Sección @refsec:interpretacióncorrelaciones. Pero antes de hacerlo, veamos cómo calcular correlaciones en R.

Cálculo de correlaciones en R

El cálculo de correlaciones en R se puede hacer usando el comando cor (). La forma más sencilla de usar el comando es especificar dos argumentos de entrada x e y, cada uno correspondiente a una de las variables. El siguiente extracto ilustra el uso básico de la función: ⁸²

cor( x = parenthood$dan.sleep, y = parenthood$dan.grump )

## [1] -0.903384

Sin embargo, la función cor () es un poco más poderosa de lo que sugiere este simple ejemplo. Por ejemplo, también se puede calcular una “matriz de correlación” completa, entre todos los pares de variables en el marco de datos: ⁸³

# correlate all pairs of variables in "parenthood":
cor( x = parenthood )  

##              dan.sleep  baby.sleep   dan.grump         day
## dan.sleep   1.00000000  0.62794934 -0.90338404 -0.09840768
## baby.sleep  0.62794934  1.00000000 -0.56596373 -0.01043394
## dan.grump  -0.90338404 -0.56596373  1.00000000  0.07647926
## day        -0.09840768 -0.01043394  0.07647926  1.00000000

Interpretación de una correlación

Naturalmente, en la vida real no se ven muchas correlaciones de 1. Entonces, ¿cómo se debe interpretar una correlación de, digamos r=.4? La respuesta honesta es que realmente depende de para qué se quiera usar los datos, y de lo fuertes que tienden a ser las correlaciones en su campo. Un amigo mío en ingeniería alguna vez argumentó que cualquier correlación inferior a .95 es completamente inútil (creo que estaba exagerando, incluso para la ingeniería). Por otro lado hay casos reales —incluso en psicología— en los que realmente deberías esperar correlaciones tan fuertes. Por ejemplo, uno de los conjuntos de datos de referencia utilizados para probar teorías de cómo las personas juzgan las similitudes es tan limpio que cualquier teoría que no pueda lograr una correlación de al menos .9 realmente no se considera exitosa. Sin embargo, al buscar (digamos) correlatos elementales de inteligencia (por ejemplo, tiempo de inspección, tiempo de respuesta), si obtienes una correlación por encima de .3 te va muy bien. En definitiva, la interpretación de una correlación depende mucho del contexto. Dicho esto, la guía aproximada en Tabla?? es bastante típico.

knitr::kable(
rbind(
c("-1.0 to -0.9" ,"Very strong", "Negative"),
c("-0.9 to -0.7", "Strong", "Negative") ,
c("-0.7 to -0.4", "Moderate", "Negative") ,
c("-0.4 to -0.2", "Weak", "Negative"),
c("-0.2 to 0","Negligible", "Negative") ,
c("0 to 0.2","Negligible", "Positive"),
c("0.2 to 0.4", "Weak", "Positive"), 
c("0.4 to 0.7", "Moderate", "Positive"), 
c("0.7 to 0.9", "Strong", "Positive"), 
c("0.9 to 1.0", "Very strong", "Positive")), col.names=c("Correlation", "Strength", "Direction"),
  booktabs = TRUE)

Correlación	Fuerza	Dirección
-1.0 a -0.9	Muy fuerte	Negativo
-0.9 a -0.7	Fuerte	Negativo
-0.7 a -0.4	Moderado	Negativo
-0.4 a -0.2	Débil	Negativo
-0.2 a 0	Despreciable	Negativo
0 a 0.2	Despreciable	Positivo
0.2 a 0.4	Débil	Positivo
0.4 a 0.7	Moderado	Positivo
0.7 a 0.9	Fuerte	Positivo
0.9 a 1.0	Muy fuerte	Positivo

Sin embargo, algo que nunca se puede recalcar lo suficiente es que siempre se debe mirar la gráfica de dispersión antes de adjuntar cualquier interpretación a los datos. Una correlación podría no significar lo que piensas que significa. La ilustración clásica de esto es “El Cuarteto de Anscombe” (??? Anscobe1973), que es una colección de cuatro conjuntos de datos. Cada conjunto de datos tiene dos variables, una X y una Y. Para los cuatro conjuntos de datos el valor medio para X es 9 y la media para Y es 7.5. Las desviaciones estándar para todas las variables X son casi idénticas, al igual que las de las variables Y. Y en cada caso la correlación entre X e Y es r=0.816. Puedes verificarlo tú mismo, ya que el conjunto de datos viene distribuido con R. Los comandos serían:

cor( anscombe$x1, anscombe$y1 )

## [1] 0.8164205 

cor( anscombe$x2, anscombe$y2 )

## [1] 0.8162365

y así sucesivamente.

Se pensaría que estos cuatro conjuntos de datos se verían bastante similares entre sí. Ellos no. Si dibujamos diagramas de dispersión de X contra Y para las cuatro variables, como se muestra en la Figura 5.11 vemos que las cuatro son espectacularmente diferentes entre sí.

Figura 5.11: Cuarteto de Anscombe. Los cuatro conjuntos de datos tienen una correlación de Pearson de r=.816, pero son cualitativamente diferentes entre sí.

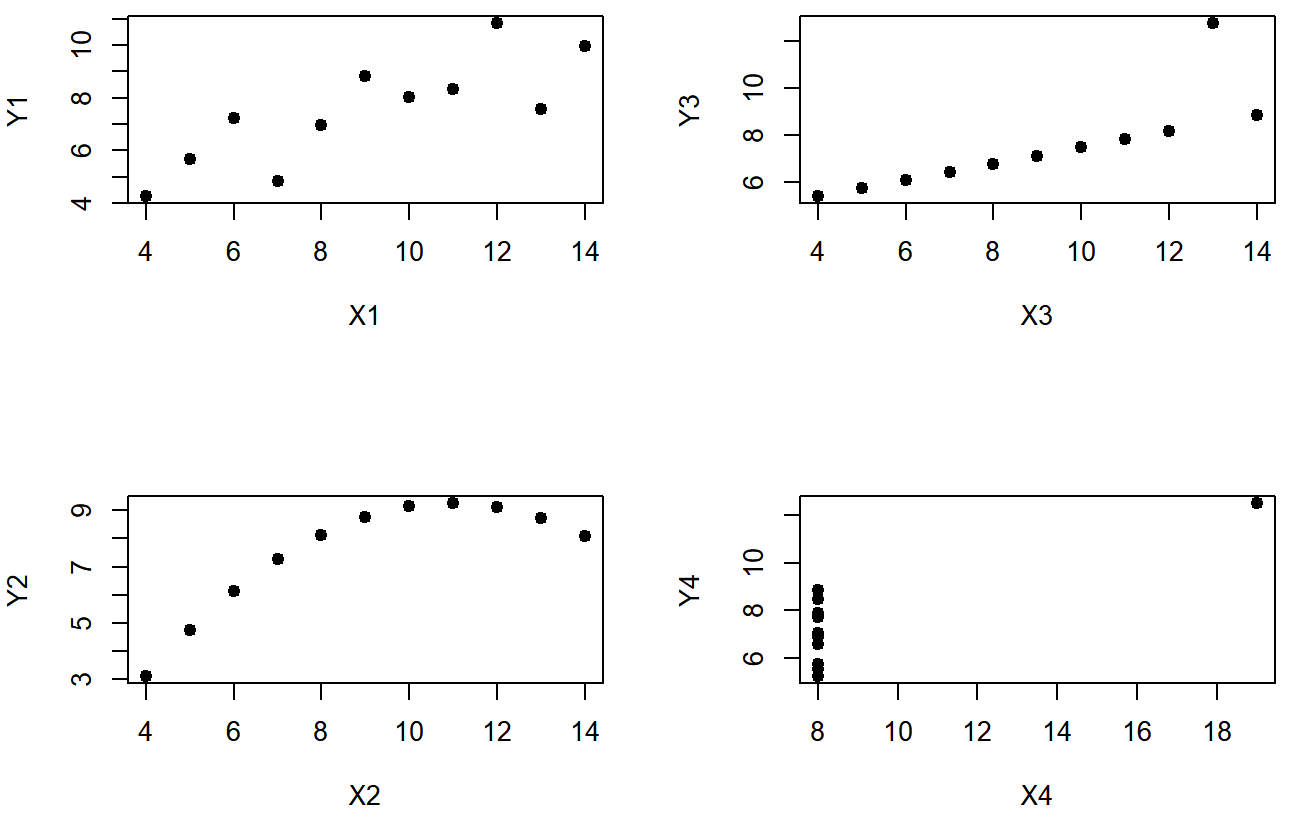
La lección aquí, que tanta gente parece olvidar en la vida real es “siempre grafica tus datos brutos”. Este será el foco del Capítulo 6.

Correlaciones de rango de Spearman

Figura 5.12: La relación entre las horas trabajadas y la calificación recibida, para un conjunto de datos de juguete que consta de sólo 10 alumnos (cada círculo corresponde a un alumno). La línea discontinua a través del medio muestra la relación lineal entre las dos variables. Esto produce una fuerte correlación de Pearson de r=.91. Sin embargo, lo interesante a tener en cuenta aquí es que en realidad existe una relación monótona perfecta entre las dos variables: en este ejemplo de juguete al menos, aumentar las horas trabajadas siempre aumenta la calificación recibida, como lo ilustra la línea continua. Esto se refleja en una correlación de Spearman de rho=1. Con un conjunto de datos tan pequeño, sin embargo, es una pregunta abierta sobre qué versión describe mejor la relación real involucrada.

El coeficiente de correlación de Pearson es útil para muchas cosas, pero sí tiene deficiencias. Destaca un tema en particular: lo que realmente mide es la fuerza de la relación lineal entre dos variables. En otras palabras, lo que te da es una medida del grado en que todos los datos tienden a caer en una sola línea, perfectamente recta. A menudo, esta es una aproximación bastante buena a lo que queremos decir cuando decimos “relación”, y así la correlación de Pearson es algo bueno para calcular. A veces, no lo es.

Una situación muy común donde la correlación de Pearson no es lo correcto para usar surge cuando un aumento en una variable X realmente se refleja en un aumento en otra variable Y, pero la naturaleza de la relación no es necesariamente lineal. Un ejemplo de esto podría ser la relación entre esfuerzo y recompensa al estudiar para un examen. Si pones cero esfuerzo (X) en aprender una materia, entonces debes esperar una calificación del 0% (Y). Sin embargo, un poco de esfuerzo provocará una mejora masiva: el solo hecho de llegar a las conferencias significa que aprendes un poco, y si solo subes a clases, y garabateas algunas cosas hacia abajo para que tu calificación pueda subir al 35%, todo sin mucho esfuerzo. Sin embargo, simplemente no obtienes el mismo efecto en el otro extremo de la escala. Como todos saben, se necesita mucho más esfuerzo para obtener una calificación del 90% que para obtener una calificación del 55%. Lo que esto significa es que, si tengo datos que analizan el esfuerzo de estudio y las calificaciones, hay muchas posibilidades de que las correlaciones de Pearson sean engañosas.

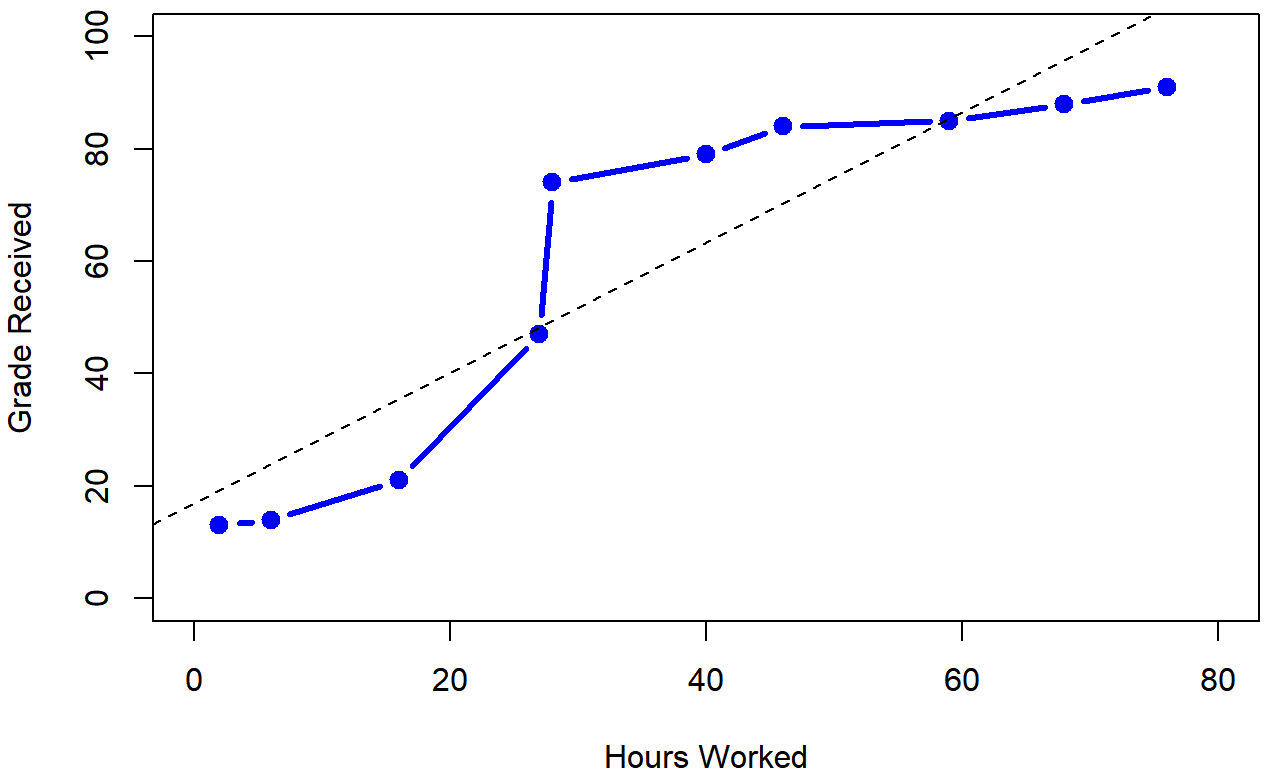
Para ilustrar, considere los datos trazados en la Figura 5.12, mostrando la relación entre las horas trabajadas y la calificación recibida para 10 estudiantes que toman alguna clase. Lo curioso de este conjunto de datos —altamente ficticio— es que aumentar tu esfuerzo siempre aumenta tu calificación. Puede ser por mucho o podría ser por poco, pero aumentar el esfuerzo nunca disminuirá tu calificación. Los datos se almacenan en Effort.rdata:

> load( "effort.Rdata" )
> who(TRUE)
   -- Name --   -- Class --   -- Size --
   effort       data.frame    10 x 2    
    $hours      numeric       10        
    $grade      numeric       10        

Los datos sin procesar se ven así:

> effort
   hours grade
1      2    13
2     76    91
3     40    79
4      6    14
5     16    21
6     28    74
7     27    47
8     59    85
9     46    84
10    68    88

Si ejecutamos una correlación estándar de Pearson, muestra una fuerte relación entre las horas trabajadas y la calificación recibida,

> cor( effort$hours, effort$grade )
[1] 0.909402

pero esto en realidad no capta la observación de que el aumento de las horas trabajadas siempre aumenta la calificación. Aquí hay un sentido en el que queremos poder decir que la correlación es perfecta pero para una noción algo diferente de lo que es una “relación”. Lo que estamos buscando es algo que capte el hecho de que aquí hay una relación ordinal perfecta. Es decir, si el estudiante 1 trabaja más horas que el estudiante 2, entonces podemos garantizar que el alumno 1 obtendrá la mejor calificación. Eso no es lo que dice en absoluto una correlación de r=.91.

¿Cómo debemos abordar esto? En realidad, es muy fácil: si buscamos relaciones ordinales, ¡todo lo que tenemos que hacer es tratar los datos como si se tratara de escala ordinal! Entonces, en lugar de medir el esfuerzo en términos de “horas trabajadas”, clasifiquemos a los 10 de nuestros alumnos en orden de horas trabajadas. Es decir, el alumno 1 hizo el menor trabajo de nadie (2 horas) por lo que obtiene el rango más bajo (rango= 1). Estudiante 4 fue el siguiente más perezoso, metiendo solo 6 horas de trabajo en todo el semestre, por lo que obtienen el siguiente rango más bajo (rango = 2). Observe que estoy usando “rank =1” para significar “rango bajo”. A veces en el lenguaje cotidiano hablamos de “rango = 1” para significar “rango superior” en lugar de “rango inferior”. Así que ten cuidado: puedes clasificar “desde el valor más pequeño hasta el valor más grande” (es decir, pequeño es igual al rango 1) o puedes clasificar “desde el valor más grande hasta el valor más pequeño” (es decir, el rango grande es igual al rango 1). En este caso, estoy clasificando de menor a mayor, porque esa es la forma predeterminada en que R lo hace. Pero en la vida real, es muy fácil olvidar de qué manera configuras las cosas, ¡así que tienes que esforzarte un poco en recordar!

Bien, entonces echemos un vistazo a nuestros alumnos cuando los clasificamos de peor a mejor en términos de esfuerzo y recompensa:

	rank (horas trabajadas)	rango (grado recibido)
estudiante	1	1
estudiante	2	10
estudiante	3	6
estudiante	4	2
estudiante	5	3
estudiante	6	5
estudiante	7	4
estudiante	8	8
estudiante	9	7
estudiante	10	9

Hm. Estos son idénticos. El estudiante que más esfuerzo se esforzó obtuvo la mejor nota, el estudiante con menor esfuerzo obtuvo la peor calificación, etc. podemos obtener R para construir estos rankings usando la función rank (), así:

> hours.rank <- rank( effort$hours )   # rank students by hours worked
> grade.rank <- rank( effort$grade )   # rank students by grade received

Como muestra la tabla anterior, estos dos rankings son idénticos, así que si ahora los correlacionamos conseguimos una relación perfecta:

> cor( hours.rank, grade.rank )
[1] 1

Lo que acabamos de reinventar es la correlación de orden de rango de Spearman, generalmente denotada ρ para distinguirla de la correlación de Pearson r. Podemos calcular la ρ de Spearman usando R de dos maneras diferentes. En primer lugar podríamos hacerlo de la manera que acabo de mostrar, usando la función rank () para construir los rankings, y luego calcular la correlación de Pearson en estos rangos. Sin embargo, eso es demasiado esfuerzo para hacer cada vez. Es mucho más fácil simplemente especificar el argumento método de la función cor ().

> cor( effort$hours, effort$grade, method = "spearman")
[1] 1

El valor predeterminado del argumento method es “pearson”, razón por la cual no tuvimos que especificarlo antes cuando estábamos haciendo correlaciones de Pearson.

función correlate ()

Como hemos visto, la función cor () funciona bastante bien, y maneja muchas de las situaciones que podrían interesarte. Una cosa que muchos principiantes encuentran frustrante, sin embargo, es el hecho de que no está construida para manejar variables no numéricas. Desde una perspectiva estadística, esto es perfectamente sensato: las correlaciones de Pearson y Spearman solo están diseñadas para funcionar para variables numéricas, por lo que la función cor () escupe un error.

Esto es lo que quiero decir. Supongamos que estaba haciendo un seguimiento de cuántas horas trabajó en un día determinado, y contó cuántas tareas completó. Si estuvieras haciendo las tareas por dinero, es posible que también quieras hacer un seguimiento de la cantidad de salario que obtuviste por cada trabajo. También sería sensato hacer un seguimiento del día de la semana en el que realmente hiciste el trabajo: la mayoría de nosotros no trabajamos tanto los sábados o domingos. Si hiciste esto durante 7 semanas, podrías terminar con un conjunto de datos que se parece a este:

> load("work.Rdata")

> who(TRUE)
   -- Name --   -- Class --   -- Size --
   work         data.frame    49 x 7    
    $hours      numeric       49        
    $tasks      numeric       49        
    $pay        numeric       49        
    $day        integer       49        
    $weekday    factor        49        
    $week       numeric       49        
    $day.type   factor        49   
    
> head(work)
  hours tasks pay day   weekday week day.type
1   7.2    14  41   1   Tuesday    1  weekday
2   7.4    11  39   2 Wednesday    1  weekday
3   6.6    14  13   3  Thursday    1  weekday
4   6.5    22  47   4    Friday    1  weekday
5   3.1     5   4   5  Saturday    1  weekend
6   3.0     7  12   6    Sunday    1  weekend

Obviamente, me gustaría saber algo sobre cómo todas estas variables se correlacionan entre sí. Podría correlacionar las horas con el pago bastante usando cor (), así:

> cor(work$hours,work$pay)
[1] 0.7604283

Pero, ¿y si quisiera una manera rápida y fácil de calcular todas las correlaciones por pares entre las variables numéricas? No puedo simplemente ingresar el marco de datos de trabajo, porque contiene dos variables factoriales, weekday y day.type. Si intento esto, me sale un error:

> cor(work)
Error in cor(work) : 'x' must be numeric

Para obtener las correlaciones que quiero usando la función cor (), es crear un nuevo marco de datos que no contenga las variables de factor, y luego alimentar ese nuevo marco de datos en la función cor (). En realidad no es muy difícil hacer eso, y voy a hablar de cómo hacerlo correctamente en la Sección @refsec:subsetdataframe. Pero sería bueno tener alguna función que sea lo suficientemente inteligente como para simplemente ignorar las variables factoriales. Ahí es donde la función correlate () en el paquete lsr puede ser útil. Si le alimenta un marco de datos que contiene factores, sabe ignorarlos y devuelve las correlaciones por pares solo entre las variables numéricas:

> correlate(work)

CORRELATIONS
============
- correlation type:  pearson 
- correlations shown only when both variables are numeric

          hours  tasks   pay    day weekday   week day.type
hours         .  0.800 0.760 -0.049       .  0.018        .
tasks     0.800      . 0.720 -0.072       . -0.013        .
pay       0.760  0.720     .  0.137       .  0.196        .
day      -0.049 -0.072 0.137      .       .  0.990        .
weekday       .      .     .      .       .      .        .
week      0.018 -0.013 0.196  0.990       .      .        .
day.type      .      .     .      .       .      .        .

La salida aquí muestra un. siempre que una de las variables no sea numérica. También muestra un. siempre que una variable se correlaciona consigo misma (no es algo significativo que hacer). La función correlate () también puede hacer correlaciones de Spearman, especificando el corr.method a usar:

> correlate( work, corr.method="spearman" )

CORRELATIONS
============
- correlation type:  spearman 
- correlations shown only when both variables are numeric

          hours  tasks   pay    day weekday   week day.type
hours         .  0.805 0.745 -0.047       .  0.010        .
tasks     0.805      . 0.730 -0.068       . -0.008        .
pay       0.745  0.730     .  0.094       .  0.154        .
day      -0.047 -0.068 0.094      .       .  0.990        .
weekday       .      .     .      .       .      .        .
week      0.010 -0.008 0.154  0.990       .      .        .
day.type      .      .     .      .       .      .        .

Obviamente, no hay nueva funcionalidad en la función correlate (), y cualquier usuario avanzado de R sería perfectamente capaz de usar la función cor () para sacar estos números. Pero si aún no te sientes cómodo con la extracción de un subconjunto de un marco de datos, la función correlate () es para ti.