6: Gráficas de dibujo
- Page ID
- 151812
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Por encima de todo mostrar los datos.
—Edward Tufte 86
Visualizar datos es una de las tareas más importantes que enfrenta el analista de datos. Es importante por dos razones distintas pero estrechamente relacionadas. En primer lugar, está la cuestión de dibujar “gráficos de presentación”: mostrar tus datos de una manera limpia y visualmente atractiva hace que sea más fácil para tu lector entender lo que intentas decirle. Igualmente importante, quizás aún más importante, es el hecho de que dibujar gráficas te ayuda a entender los datos. Para ello, es importante dibujar “gráficos exploratorios” que te ayuden a conocer los datos a medida que los analizas. Estos puntos pueden parecer bastante obvios, pero no puedo contar la cantidad de veces que he visto a la gente olvidarlos.
## Warning: package 'HistData' was built under R version 3.5.2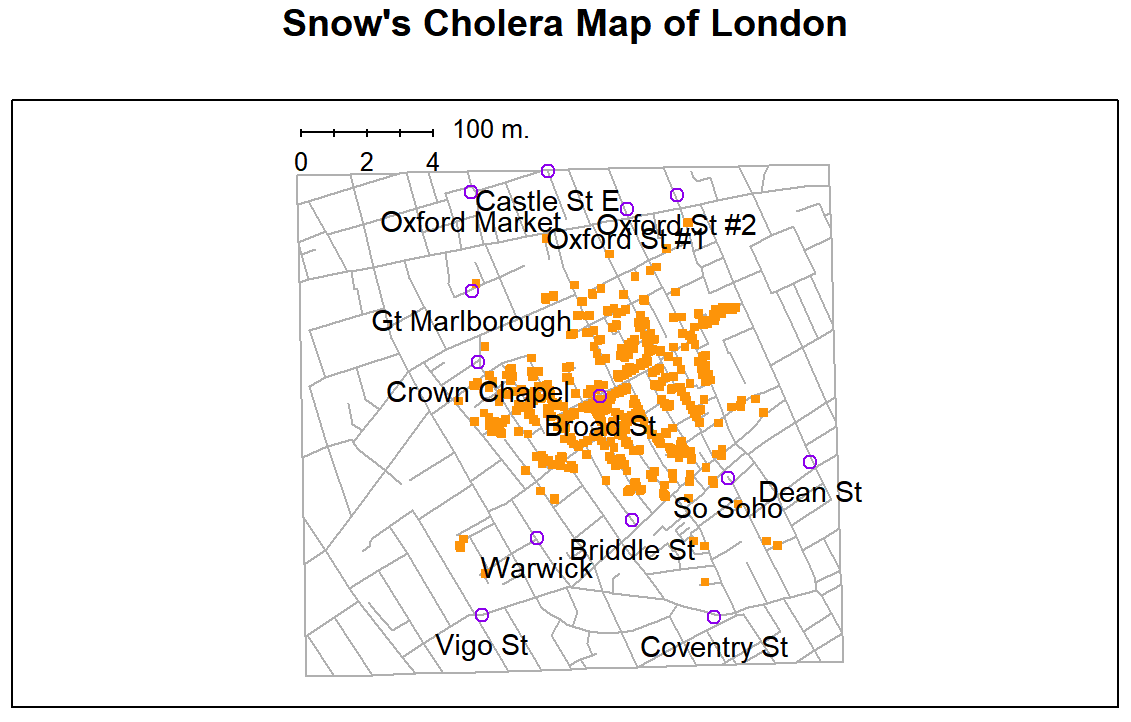
HistData @ [Friendly2011], y se dibujó usando pequeñas alteraciones en los comandos proporcionados en los archivos de ayuda. Ten en cuenta que el mapa original dibujado a mano de Snow usaba diferentes símbolos y etiquetas, pero ya entiendes la idea.Para dar una idea de la importancia de este capítulo, quiero comenzar con una ilustración clásica de lo poderosa que puede ser una buena gráfica. Para ello, la Figura 6.1 muestra un redibujo de una de las visualizaciones de datos más famosas de todos los tiempos: el mapa de 1854 de muertes por cólera de John Snow. El mapa es elegante en su sencillez. Al fondo tenemos un mapa de calles, que ayuda a orientar al espectador. En la parte superior, vemos una gran cantidad de pequeños puntos, cada uno representando la ubicación de un caso de cólera. Los símbolos más grandes muestran la ubicación de las bombas de agua, etiquetadas por su nombre. Incluso la inspección más casual de la gráfica deja muy claro que la fuente del brote es casi con certeza la bomba de Broad Street. Al ver esta gráfica, el Dr. Snow dispuso que le quitaran el mango de la bomba, poniendo fin al brote que había matado a más de 500 personas. Tal es el poder de una buena visualización de datos.
Los objetivos de este capítulo son dobles: en primer lugar, discutir varias gráficas bastante estándar que utilizamos mucho a la hora de analizar y presentar datos, y en segundo lugar, mostrarte cómo crear estas gráficas en R. Las gráficas en sí tienden a ser bastante sencillas, por lo que en ese sentido este capítulo es bastante sencillo. Donde la gente suele tener dificultades es aprender a producir gráficas, y especialmente, aprender a producir buenas gráficas. 87 Afortunadamente, aprender a dibujar gráficas en R es razonablemente simple, siempre y cuando no seas demasiado exigente con el aspecto de tu gráfica. A lo que me refiero cuando digo esto es que R tiene muchas funciones gráficas muy buenas, y la mayoría de las veces se puede producir un gráfico limpio y de alta calidad sin tener que aprender mucho sobre los detalles de bajo nivel de cómo R maneja los gráficos. Desafortunadamente, en esas ocasiones en las que sí quieres hacer algo no estándar, o si necesitas hacer cambios muy específicos en la figura, en realidad necesitas aprender un poco sobre estos detalles; y esos detalles son complicados y aburridos. Con eso en mente, la estructura de este capítulo es la siguiente: Comenzaré dándote una visión general muy rápida de cómo funcionan los gráficos en R. Luego discutiré varios tipos diferentes de gráficas y cómo dibujarlas, además de mostrarte los conceptos básicos de cómo personalizar estas tramas. Luego hablaré con más detalle sobre los gráficos R, discutiendo algunos de esos temas complicados y aburridos. En una versión futura de este libro, pretendo terminar este capítulo hablando de lo que hace que una gráfica sea buena o mala, pero aún no he tenido tiempo de escribir esa sección.


