10.5: Estimación de un Intervalo de Confianza
- Page ID
- 151461
Estadísticas significa no tener que decir que estás seguro — Origen desconocido 154 pero nunca he encontrado la fuente original.
Hasta este punto en este capítulo, he esbozado los fundamentos de la teoría del muestreo en los que se basan los estadísticos para hacer conjeturas sobre los parámetros de la población a partir de una muestra de datos. Como ilustra esta discusión, una de las razones por las que necesitamos toda esta teoría de muestreo es que cada conjunto de datos nos deja con un poco de incertidumbre, por lo que nuestras estimaciones nunca van a ser perfectamente precisas. Lo que ha estado faltando en esta discusión es un intento de cuantificar la cantidad de incertidumbre que se atribuye a nuestra estimación. No basta con poder adivinar que, digamos, el coeficiente intelectual medio de los estudiantes de licenciatura en psicología es de 115 (sí, acabo de inventar ese número). También queremos poder decir algo que exprese el grado de certeza que tenemos en nuestra conjetura. Por ejemplo, sería bueno poder decir que hay un 95% de posibilidades de que la verdadera media se encuentre entre 109 y 121. El nombre para esto es un intervalo de confianza para la media.
Armado con una comprensión de las distribuciones de muestreo, construir un intervalo de confianza para la media es bastante fácil. Así es como funciona. Supongamos que la media verdadera de la población es μ y la desviación estándar es σ. Acabo de terminar de dirigir mi estudio que tiene N participantes, y el coeficiente intelectual medio entre esos participantes es\(\bar{X}\). Sabemos por nuestra discusión del teorema del límite central (Sección 10.3.3 que la distribución muestral de la media es aproximadamente normal. También sabemos por nuestra discusión sobre la distribución normal Sección 9.5 que existe un 95% de probabilidad de que una cantidad normalmente distribuida caiga dentro de dos desviaciones estándar de la media verdadera. Para ser más precisos, podemos usar la función qnorm () para calcular los percentiles 2.5 y 97.5 de la distribución normal
qnorm( p = c(.025, .975) )## [1] -1.959964 1.959964Bien, entonces mentí antes. La respuesta más correcta es que 95% de probabilidad de que una cantidad normalmente distribuida caiga dentro de 1.96 desviaciones estándar de la media verdadera. A continuación, recordemos que la desviación estándar de la distribución muestral es referida como el error estándar, y el error estándar de la media se escribe como SEM. Cuando juntamos todas estas piezas, aprendemos que existe una probabilidad del 95% de que la media muestral\(\bar{X}\) que hemos observado se encuentre dentro de 1.96 errores estándar de la media poblacional. Matemáticamente, escribimos esto como:
μ− (1.96×SEM) ≤\(\bar{X}\) ≤ μ+ (1.96×SEM)
donde el SEM es igual a σ/\(\sqrt{N}\), y podemos estar 95% seguros de que esto es cierto. Sin embargo, eso no es responder a la pregunta que realmente nos interesa. La ecuación anterior nos dice qué debemos esperar de la media muestral, dado que sabemos cuáles son los parámetros poblacionales. Lo que queremos es tener este trabajo al revés: queremos saber qué debemos creer sobre los parámetros poblacionales, dado que hemos observado una muestra en particular. No obstante, no es demasiado difícil hacer esto. Usando un poco de álgebra de secundaria, una forma furtiva de reescribir nuestra ecuación es así:
\(\bar{X}\)− (1.96×SEM) ≤ μ ≤\(\bar{X}\) + (1.96×SEM)
Lo que esto está diciendo es que el rango de valores tiene una probabilidad del 95% de contener la media poblacional μ. Nos referimos a este rango como un intervalo de confianza del 95%, denotado IC 95. En resumen, mientras N sea lo suficientemente grande —lo suficientemente grande como para que creamos que la distribución muestral de la media es normal— entonces podemos escribir esto como nuestra fórmula para el intervalo de confianza del 95%:
\(\mathrm{CI}_{95}=\bar{X} \pm\left(1.96 \times \dfrac{\sigma}{\sqrt{N}}\right)\)
Por supuesto, no hay nada especial en el número 1.96: simplemente pasa a ser el multiplicador que necesitas usar si quieres un intervalo de confianza del 95%. Si hubiera querido un intervalo de confianza del 70%, podría haber usado la función qnorm () para calcular los cuantiles 15 y 85:
qnorm( p = c(.15, .85) )## [1] -1.036433 1.036433y así la fórmula para CI 70 sería la misma que la fórmula para CI 95 excepto que usaríamos 1.04 como nuestro número mágico en lugar de 1.96.
ligero error en la fórmula
Como siempre, mentí. La fórmula que he dado anteriormente para el intervalo de confianza del 95% es aproximadamente correcta, pero pasé por alto un detalle importante en la discusión. Observe mi fórmula requiere que use el error estándar de la media, SEM, que a su vez requiere que use la verdadera desviación estándar de población σ. Sin embargo, en la Sección @ref (puntoestimaciones destaqué el hecho de que en realidad no conocemos los verdaderos parámetros poblacionales. Debido a que no conocemos el verdadero valor de σ, tenemos que usar una estimación de la desviación estándar de la población\(\hat{σ}\) en su lugar. Esto es bastante sencillo de hacer, pero esto tiene la consecuencia de que necesitamos usar los cuantiles de la distribución t en lugar de la distribución normal para calcular nuestro número mágico; y la respuesta depende del tamaño de la muestra. Cuando N es muy grande, obtenemos prácticamente el mismo valor usando qt () que lo haríamos si usáramos qnorm ()...
N <- 10000 # suppose our sample size is 10,000
qt( p = .975, df = N-1) # calculate the 97.5th quantile of the t-dist## [1] 1.960201Pero cuando N es pequeño, obtenemos un número mucho mayor cuando usamos la distribución t:
N <- 10 # suppose our sample size is 10
qt( p = .975, df = N-1) # calculate the 97.5th quantile of the t-dist## [1] 2.262157No hay nada demasiado misterioso en lo que está pasando aquí. Valores más grandes significan que el intervalo de confianza es más amplio, lo que indica que estamos más inseguros sobre cuál es realmente el verdadero valor de μ. Cuando usamos la distribución t en lugar de la distribución normal, obtenemos números más grandes, lo que indica que tenemos más incertidumbre. ¿Y por qué tenemos esa incertidumbre extra? Bueno, porque nuestra estimación de la desviación estándar de la población ^σ podría estar equivocada! Si está mal, implica que estamos un poco menos seguros de cómo se ve realmente nuestra distribución muestral de la media... y esta incertidumbre termina reflejándose en un intervalo de confianza más amplio.
Interpretación de un intervalo de confianza
Lo más difícil de los intervalos de confianza es entender lo que significan. Siempre que las personas se encuentran por primera vez con intervalos de confianza, el primer instinto es casi siempre decir que “hay una probabilidad del 95% de que la verdadera media se encuentre dentro del intervalo de confianza”. Es simple, y parece plasmar la idea de sentido común de lo que significa decir que tengo “95% de confianza”. Desafortunadamente, no está del todo bien. La definición intuitiva se basa en gran medida en sus propias creencias personales sobre el valor de la media poblacional. Digo que tengo un 95% de confianza porque esas son mis creencias. En la vida cotidiana eso está perfectamente bien, pero si recuerdas volver a la Sección 9.2, notarás que hablar de creencia personal y confianza es una idea bayesiana. Personalmente (hablando como bayesiano) no tengo ningún problema con la idea de que la frase “95% de probabilidad” está permitida para referirse a una creencia personal. Sin embargo, los intervalos de confianza no son herramientas bayesianas. Como todo lo demás en este capítulo, los intervalos de confianza son herramientas frecuentistas, y si vas a usar métodos frecuentistas entonces no es apropiado adjuntarles una interpretación bayesiana. Si usas métodos frecuentistas, ¡debes adoptar interpretaciones frecuentistas!
Bien, así que si esa no es la respuesta correcta, ¿qué es? Recuerden lo que dijimos sobre la probabilidad frecuentista: la única forma en que se nos permite hacer “declaraciones de probabilidad” es hablar de una secuencia de eventos, y contar las frecuencias de diferentes tipos de eventos. Desde esa perspectiva, la interpretación de un intervalo de confianza del 95% debe tener algo que ver con la replicación. Específicamente: si replicamos el experimento una y otra vez y calculamos un intervalo de confianza del 95% para cada replicación, entonces el 95% de esos intervalos contendría la media verdadera. De manera más general, 95% de todos los intervalos de confianza construidos con este procedimiento deben contener la media poblacional verdadera. Esta idea se ilustra en la Figura 10.13, que muestra 50 intervalos de confianza construidos para un experimento de “medir 10 puntuaciones de CI” (panel superior) y otros 50 intervalos de confianza para un experimento de “medir 25 puntuaciones de CI” (panel inferior). Un poco fortuitamente, a través de las 100 réplicas que simulé, resultó que exactamente 95 de ellas contenían la verdadera media.
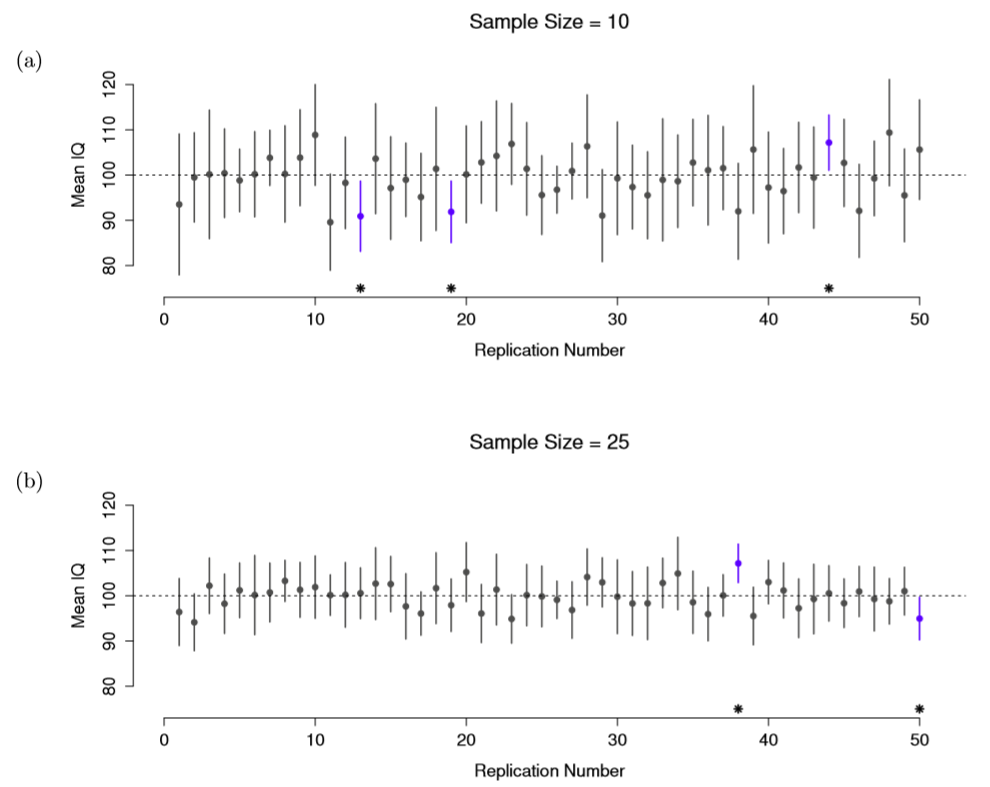
La diferencia crítica aquí es que la afirmación bayesiana hace una declaración de probabilidad sobre la media poblacional (es decir, se refiere a nuestra incertidumbre sobre la media poblacional), lo cual no está permitido bajo la interpretación frecuentista de la probabilidad porque ¡no se puede “replicar” a una población! En el reclamo frecuentista, la media poblacional es fija y no se pueden hacer afirmaciones probabilísticas al respecto. Los intervalos de confianza, sin embargo, son repetibles para que podamos replicar experimentos. Por lo tanto, se permite a un frecuentista hablar sobre la probabilidad de que el intervalo de confianza (una variable aleatoria) contenga la media verdadera; pero no se le permite hablar de la probabilidad de que la verdadera media poblacional (no un evento repetible) se encuentre dentro del intervalo de confianza.
Sé que esto parece un poco pedante, pero sí importa. Importa porque la diferencia en la interpretación conduce a una diferencia en las matemáticas. Existe una alternativa bayesiana a los intervalos de confianza, conocidos como intervalos creíbles. En la mayoría de las situaciones, los intervalos creíbles son bastante similares a los intervalos de confianza, pero en otros casos son drásticamente diferentes. Sin embargo, como prometí, hablaré más sobre la perspectiva bayesiana en el Capítulo 17.
Cálculo de intervalos de confianza en R
Por lo que puedo decir, los paquetes core en R no incluyen una función simple para calcular los intervalos de confianza para la media. Incluyen muchas funciones complicadas y extremadamente poderosas que se pueden usar para calcular intervalos de confianza asociados con muchas cosas diferentes, como la función confint () que usaremos en el Capítulo 15. Pero me imagino que cuando estás aprendiendo estadísticas por primera vez, podría ser útil comenzar con algo más sencillo. Como consecuencia, el paquete lsr incluye una función llamada ciMean () que puede usar para calcular sus intervalos de confianza. Hay dos argumentos que quizás quieras especificar: 155
x. Este debe ser un vector numérico que contenga los datos.conf. Este debe ser un número, especificando el nivel de confianza. Por defecto,conf = .95, ya que los intervalos de confianza del 95% son el estándar de facto en psicología.
Entonces, por ejemplo, si cargo el archivo AFL24.rData, calcule el intervalo de confianza asociado con la asistencia media:
> ciMean( x = afl$attendance )
2.5% 97.5%
31597.32 32593.12 Ojalá eso quede bastante claro.
Trazado de intervalos de confianza en R
Hay varias formas diferentes de dibujar gráficas que muestran intervalos de confianza como barras de error. Aquí voy a mostrar tres versiones, pero esto ciertamente no agota las posibilidades. Al hacerlo, lo que estoy asumiendo es que se quiere dibujar es una gráfica que muestre las medias e intervalos de confianza para una variable, desglosada por diferentes niveles de una segunda variable. Por ejemplo, en nuestros datos afl que discutimos anteriormente, podríamos estar interesados en trazar la asistencia promedio por año. Voy a hacer esto usando dos funciones diferentes, bargraph.ci () y lineplot.ci () (ambas están en el paquete sciplot). Suponiendo que haya instalado estos paquetes en su sistema (consulte la Sección 4.2 si ha olvidado cómo hacerlo), deberá cargarlos. También necesitarás cargar el paquete lsr, porque haremos uso de la función ciMean () para calcular realmente los intervalos de confianza
load( "./rbook-master/data/afl24.Rdata" ) # contains the "afl" data frame
library( sciplot ) # bargraph.CI() and lineplot.CI() functions
library( lsr ) # ciMean() functionAquí se explica cómo trazar las medias y los intervalos de confianza dibujados usando Bargraph.ci ().
bargraph.CI( x.factor = year, # grouping variable
response = attendance, # outcome variable
data = afl, # data frame with the variables
ci.fun= ciMean, # name of the function to calculate CIs
xlab = "Year", # x-axis label
ylab = "Average Attendance" # y-axis label
)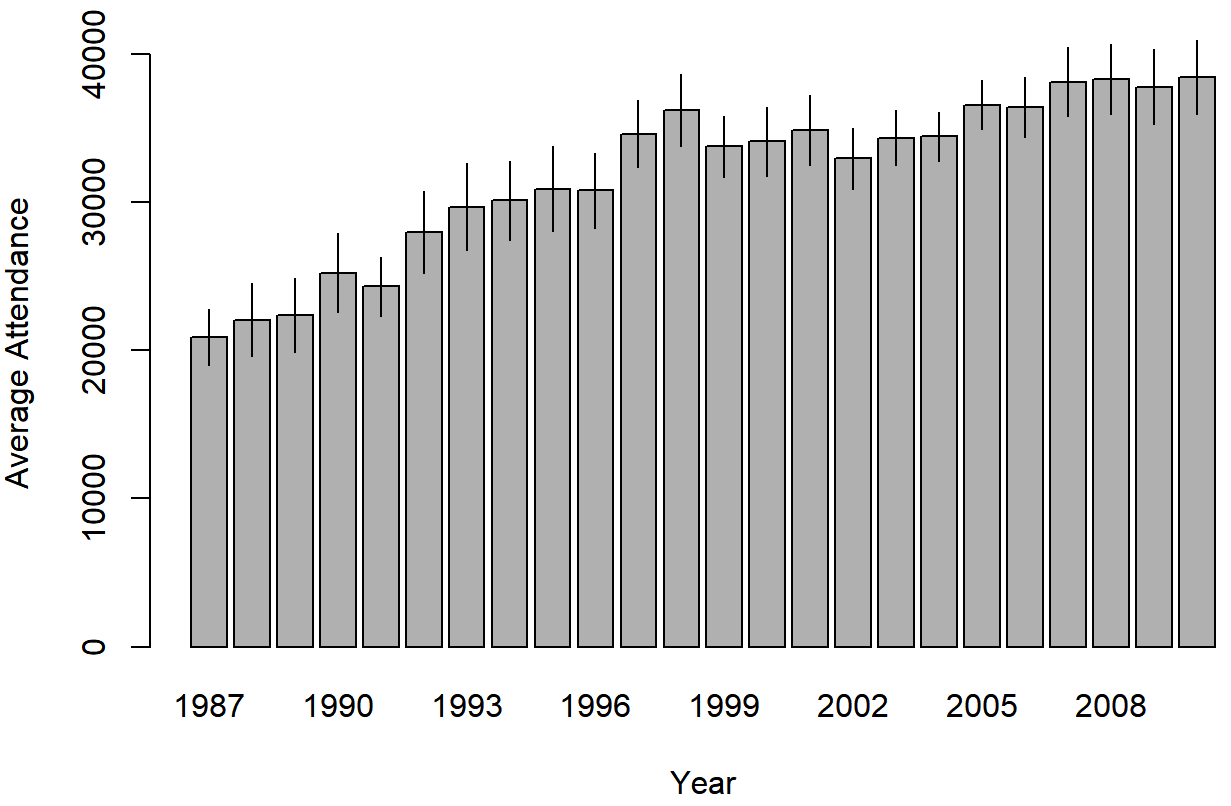
asistencia de AFL, trazados por separado para cada año de 1987 a 2010. Esta gráfica se dibujó utilizando la función Bargraph.ci ().Podemos usar los mismos argumentos al llamar a la función linePlot.ci ():
lineplot.CI( x.factor = year, # grouping variable
response = attendance, # outcome variable
data = afl, # data frame with the variables
ci.fun= ciMean, # name of the function to calculate CIs
xlab = "Year", # x-axis label
ylab = "Average Attendance" # y-axis label
)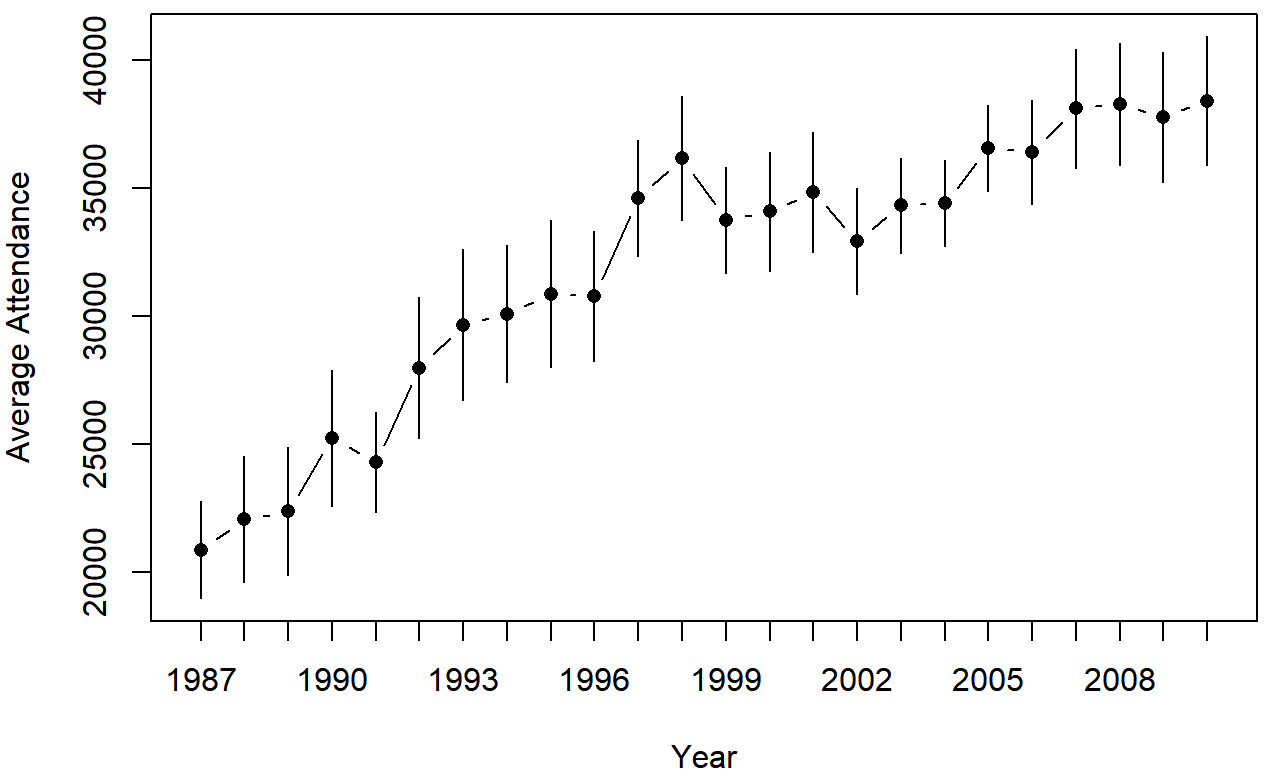
asistencia de AFL, trazados por separado para cada año de 1987 a 2010. Esta gráfica se dibujó usando la función Lineplot.ci ().

