13.3: La prueba t de Muestras Independientes (Prueba de Student)
- Page ID
- 151833
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aunque la prueba t de una muestra tiene sus usos, no es el ejemplo más típico de una prueba t 189. Una situación mucho más común surge cuando tienes dos grupos diferentes de observaciones. En psicología, esto tiende a corresponder a dos grupos diferentes de participantes, donde cada grupo corresponde a una condición diferente en tu estudio. Para cada persona en el estudio, se mide alguna variable de resultado de interés, y la pregunta de investigación que se está haciendo es si los dos grupos tienen o no la misma media poblacional. Esta es la situación para la que está diseñada la prueba t de muestras independientes.
datos
Supongamos que tenemos 33 estudiantes tomando las conferencias de estadística del Dr. Harpo, y el Dr. Harpo no califica a una curva. En realidad, la calificación del Dr. Harpo es un poco misteriosa, así que realmente no sabemos nada sobre cuál es la calificación promedio para la clase en su conjunto. Hay dos tutores para la clase, Anastasia y Bernadette. Hay N 1 =15 alumnos en las tutorías de Anastasia, y N 2 =18 en las tutorías de Bernadette. La pregunta de investigación que me interesa es si Anastasia o Bernadette es una mejor tutora, o si no hace mucha diferencia. El Dr. Harpo me envía por correo electrónico las calificaciones del curso, en el archivo Harpo.rdata. Como de costumbre, cargaré el archivo y echaré un vistazo a qué variables contiene:
load( "./rbook-master/data/harpo.Rdata" )
str(harpo)## 'data.frame': 33 obs. of 2 variables:
## $ grade: num 65 72 66 74 73 71 66 76 69 79 ...
## $ tutor: Factor w/ 2 levels "Anastasia","Bernadette": 1 2 2 1 1 2 2 2 2 2 ...Como podemos ver, hay un solo marco de datos con dos variables, grado y tutor. La variable grado es un vector numérico, que contiene las calificaciones de todos los N=33 estudiantes que toman la clase del Dr. Harpo; la variable tutor es un factor que indica quién fue el tutor de cada alumno. A continuación se muestran las seis primeras observaciones de este conjunto de datos:
head( harpo )## grade tutor
## 1 65 Anastasia
## 2 72 Bernadette
## 3 66 Bernadette
## 4 74 Anastasia
## 5 73 Anastasia
## 6 71 BernadettePodemos calcular medias y desviaciones estándar, utilizando las funciones mean () y sd (). En lugar de mostrar la salida R, aquí hay una pequeña tabla de resumen agradable:
| media | std dev | N | |
|---|---|---|---|
| Alumnos de Anastasia | 74.53 | 9.00 | 15 |
| Alumnos de Bernadette | 69.06 | 5.77 | 18 |
Para darle una idea más detallada de lo que está pasando aquí, he trazado histogramas que muestran la distribución de calificaciones para ambos tutores (Figura 13.6 y 13.7). La inspección de estos histogramas sugiere que los estudiantes de la clase de Anastasia pueden estar obteniendo calificaciones ligeramente mejores en promedio, aunque también parecen un poco más variables.
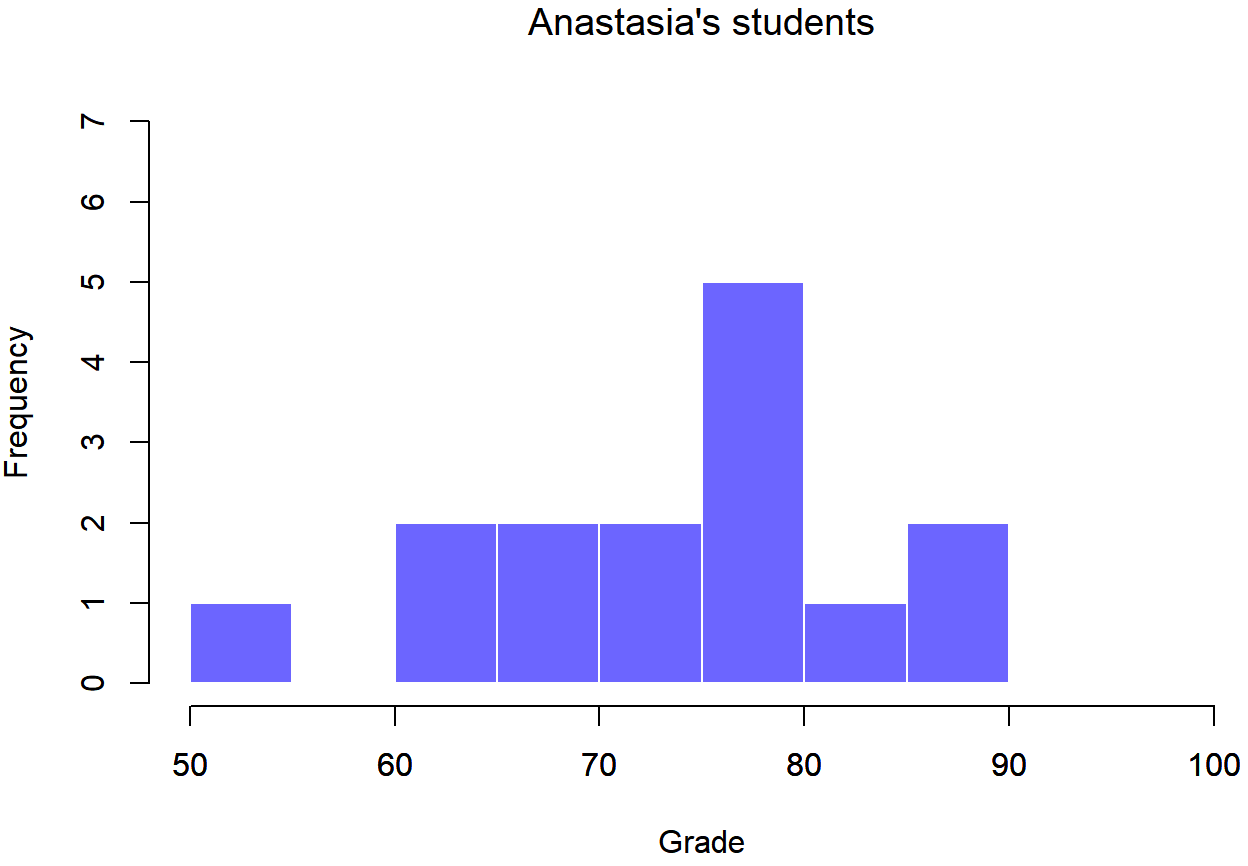
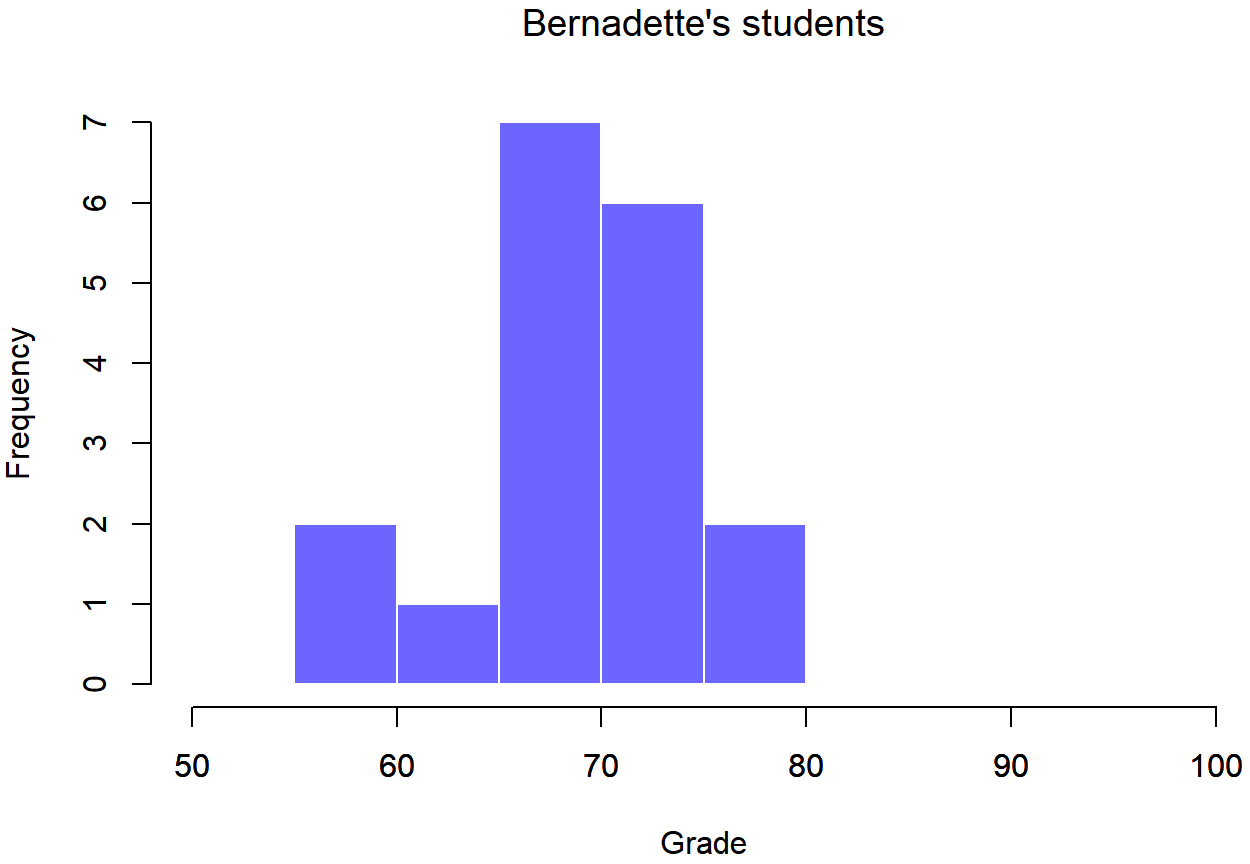
Aquí hay una gráfica más simple que muestra las medias y los intervalos de confianza correspondientes para ambos grupos de estudiantes (Figura 13.8).
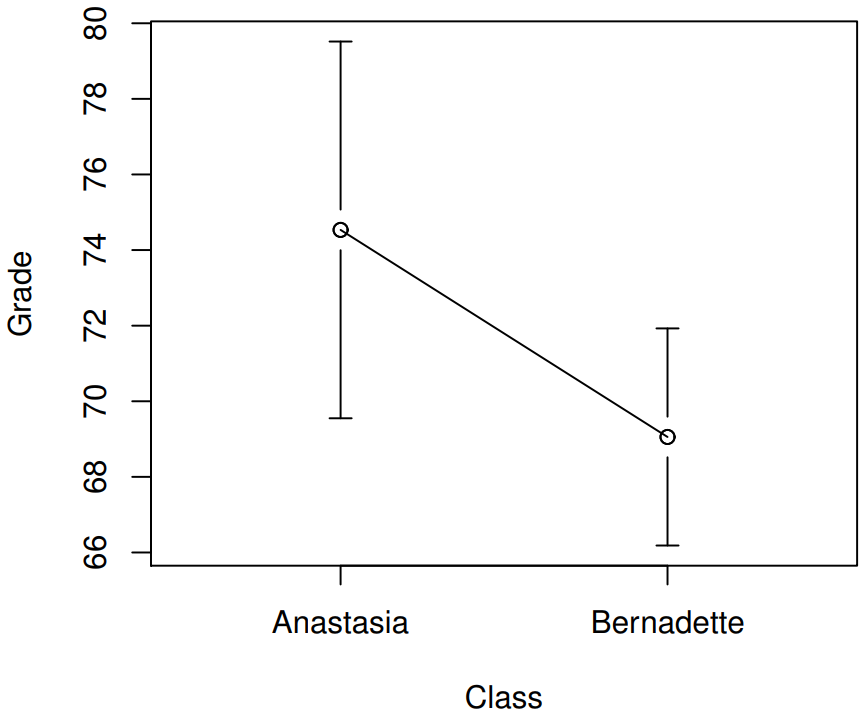
Presentamos la prueba
La prueba t de muestras independientes viene en dos formas diferentes, la de Student y la de Welch, la prueba t original de Student, que es la que describiré en esta sección, es la más simple de las dos, pero se basa en suposiciones mucho más restrictivas que la prueba t de Welch. Suponiendo por el momento que se quiere ejecutar una prueba bilateral, el objetivo es determinar si se extraen dos “muestras independientes” de datos de poblaciones con la misma media (la hipótesis nula) o medias diferentes (la hipótesis alternativa). Cuando decimos muestras “independientes”, lo que realmente queremos decir aquí es que no hay una relación especial entre las observaciones en las dos muestras. Esto probablemente no tenga mucho sentido en este momento, pero será más claro cuando lleguemos a hablar de la prueba t de muestras pareadas más adelante. Por ahora, solo señalemos que si tenemos un diseño experimental donde los participantes se asignan aleatoriamente a uno de dos grupos, y queremos comparar el rendimiento medio de los dos grupos en alguna medida de resultado, entonces lo que buscamos es una prueba t de muestras independientes (en lugar de una prueba t de muestras pareadas).
Bien, entonces vamos a dejar que μ 1 denote la verdadera media de población para el grupo 1 (por ejemplo, los estudiantes de Anastasia), y μ 2 será la verdadera media poblacional para el grupo 2 (por ejemplo, los estudiantes de Bernadette), 190 y como de costumbre dejaremos\(\bar{X}_{1}\) y\(\bar{X}_{2}\) denotaremos las medias de muestra observadas para ambos grupos. Nuestra hipótesis nula establece que las dos medias poblacionales son idénticas (μ 1 =μ 2) y la alternativa a esto es que no lo son (μ 1 ≠ μ 2). Escrito en matemática-ese, esto es...
H 0:μ 1 =μ 2
H 1:μ 1 ≠ μ 2
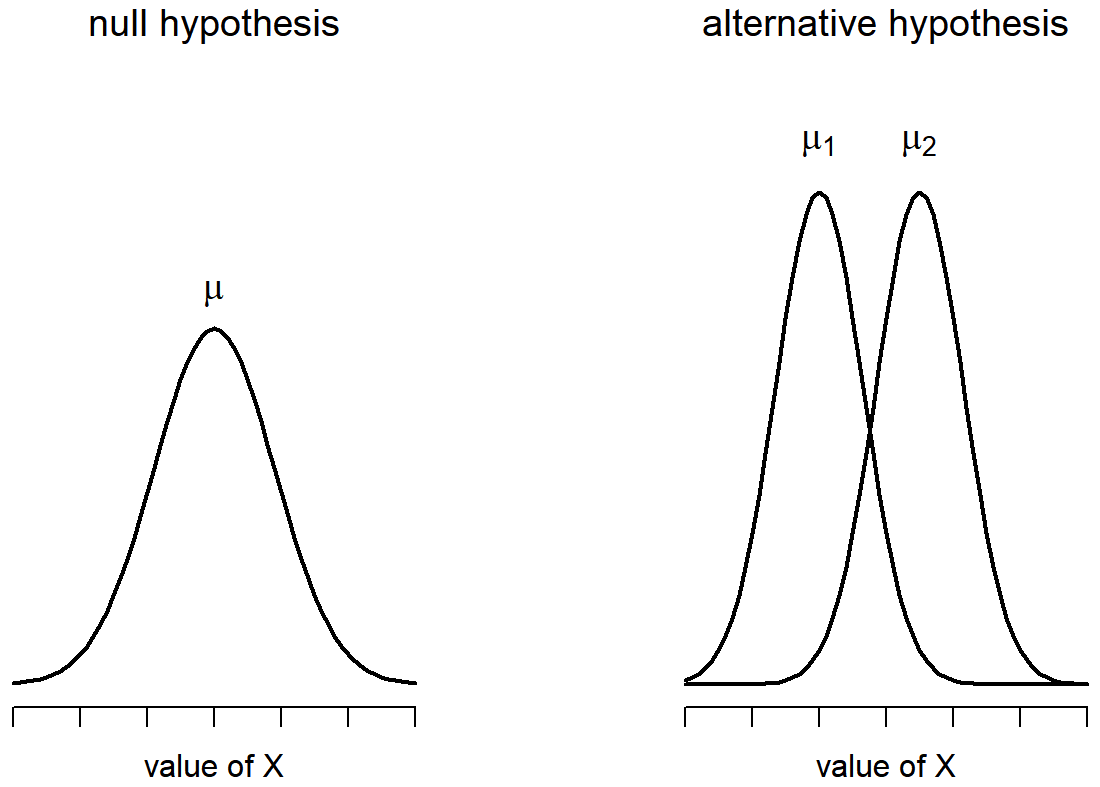
Para construir una prueba de hipótesis que maneje este escenario, comenzamos señalando que si la hipótesis nula es verdadera, entonces la diferencia entre las medias de la población es exactamente cero, μ 1 −μ 2 =0 Como consecuencia, una estadística de prueba diagnóstica se basará en la diferencia entre las dos medias de la muestra. Porque si la hipótesis nula es cierta, entonces esperaríamos
\(\bar{X}_{1}\)-\(\bar{X}_{2}\)
estar bastante cerca de cero. Sin embargo, al igual que vimos con nuestras pruebas de una muestra (es decir, la prueba z de una muestra y la prueba t de una muestra) tenemos que ser precisos sobre exactamente qué tan cerca de cero esta diferencia
\(\ t ={\bar{X}_1 - \bar{X}_2 \over SE}\)
Solo tenemos que averiguar cuál es realmente esta estimación de error estándar. Esto es un poco más complicado de lo que fue el caso de cualquiera de las dos pruebas que hemos visto hasta ahora, así que tenemos que revisarlo mucho más cuidadosamente para entender cómo funciona.
“estimación agrupada” de la desviación estándar
En la “prueba t de Student” original, hacemos la suposición de que los dos grupos tienen la misma desviación estándar poblacional: es decir, independientemente de que las medias poblacionales sean las mismas, asumimos que las desviaciones estándar poblacionales son idénticas, σ 1 =σ 2. Como estamos asumiendo que las dos desviaciones estándar son las mismas, bajamos los subíndices y nos referimos a ambos como σ. ¿Cómo debemos estimar esto? ¿Cómo se debe construir una sola estimación de una desviación estándar cuando tenemos dos muestras? La respuesta es, básicamente, los promediamos. Bueno, algo así como. En realidad, lo que hacemos es tomar un promedio ponderado de las estimaciones de varianza, que utilizamos como nuestra estimación agrupada de la varianza. El peso asignado a cada muestra es igual al número de observaciones en esa muestra, menos 1. Matemáticamente, podemos escribir esto como
\(\ \omega_{1}\)=N 1 −1
\(\ \omega_{2}\)=N 2 −1
Ahora que hemos asignado pesos a cada muestra, calculamos la estimación agrupada de la varianza tomando el promedio ponderado de las dos estimaciones de varianza,\(\ \hat{\sigma_1}^2\) y\(\ \hat{\sigma_2}^2\)
\(\ \hat{\sigma_p}^2 ={ \omega_{1}\hat{\sigma_1}^2+\omega_{2}\hat{\sigma_2}^2 \over \omega_{1}+\omega_{2}}\)
Finalmente, convertimos la estimación de varianza agrupada en una estimación de desviación estándar agrupada, tomando la raíz cuadrada. Esto nos da la siguiente fórmula para\(\ \hat{\sigma_p}\),
\(\ \hat{\sigma_p} =\sqrt{\omega_1\hat{\sigma_1}^2+\omega_2\hat{\sigma_2}^2\over \omega_1+\omega_2} \)
Y si sustitues mentalmente\(\ \omega_1\) =N1−1 y\(\ \omega_2\) =N2−1 en esta ecuación obtienes una fórmula muy fea; una fórmula muy fea que en realidad parece ser la forma “estándar” de describir la estimación de desviación estándar agrupada. Sin embargo, no es mi forma favorita de pensar sobre las desviaciones estándar agrupadas. 191
misma estimación agrupada, descrita de manera diferente
Prefiero pensarlo así. Nuestro conjunto de datos corresponde realmente a un conjunto de N observaciones, que se clasifican en dos grupos. Entonces usemos la notación X ik para referirnos a la calificación recibida por el alumno i-ésimo en el k-ésimo grupo tutorial: es decir, X 11 es la calificación recibida por el primer alumno en la clase de Anastasia, X 21 es su segundo alumno, y así sucesivamente. Y tenemos dos medias grupales separadas\(\ \bar{X_1}\) y\(\ \bar{X_2}\), a las que podríamos referirnos “genéricamente” usando la notación\(\ \bar{X_k}\), es decir, la calificación media para el k-ésimo grupo tutorial. Hasta el momento, tan bien. Ahora, ya que cada alumno cae en una de las dos tutorías, y así podemos describir su desviación de la media grupal como la diferencia
\(\ X_{ik} - \bar{X_k}\)
Entonces, ¿por qué no solo usar estas desviaciones (es decir, la medida en que la calificación de cada alumno difiere de la nota media en su tutorial?) Recuerda, una varianza es solo el promedio de un montón de desviaciones cuadradas, así que hagámoslo. Matemáticamente, podríamos escribirlo así:
\(\ ∑_{ik} (X_{ik}-\bar{X}_k)^2 \over N \)
donde la notación “ik” es una forma perezosa de decir “calcular una suma mirando a todos los alumnos en todas las tutorías”, ya que cada “ik” corresponde a un alumno. 192 Pero, como vimos en el Capítulo 10, calcular la varianza dividiendo por N produce una estimación sesgada de la varianza poblacional. Y anteriormente, necesitábamos dividir por N−1 para arreglar esto. Sin embargo, como mencioné en ese momento, la razón por la que existe este sesgo es porque la estimación de varianza se basa en la media de la muestra; y en la medida en que la media de la muestra no es igual a la media poblacional, puede sesgar sistemáticamente nuestra estimación de la varianza. ¡Pero esta vez estamos confiando en dos medios de muestra! ¿Significa esto que tenemos más sesgo? Sí, sí lo hace. ¿Y esto significa que ahora necesitamos dividir por N−2 en lugar de N−1, para poder calcular nuestra estimación de varianza agrupada? Por qué, sí...
\(\hat{\sigma}_{p}\ ^{2}=\dfrac{\sum_{i k}\left(X_{i k}-X_{k}\right)^{2}}{N-2}\)
Ah, y si tomas la raíz cuadrada de esto entonces obtienes\(\ \hat{\sigma_{P}}\), la estimación de desviación estándar agrupada. En otras palabras, el cálculo de la desviación estándar agrupada no es nada especial: no es terriblemente diferente al cálculo de la desviación estándar regular.
Completar la prueba
Independientemente de la forma en que quieras pensarlo, ahora tenemos nuestra estimación agrupada de la desviación estándar. A partir de ahora, dejaré caer el tonto subíndice p, y solo referirme a esta estimación como\(\ \hat{\sigma}\). Genial. Ahora volvamos a pensar en la sangrienta prueba de hipótesis, ¿de acuerdo? Toda nuestra razón para calcular esta estimación agrupada fue que sabíamos que sería útil a la hora de calcular nuestra estimación de error estándar. Pero, ¿error estándar de qué? En la prueba t de una muestra, fue el error estándar de la media muestral, SE (\(\ \bar{X}\)), y desde SE (\(\ \bar{X}=\sigma/ \sqrt{N}\)así era el denominador de nuestro estadístico t). Esta vez, sin embargo, tenemos dos medias de muestra. Y lo que nos interesa, específicamente, es la diferencia entre los dos\(\ \bar{X_1}\) -\(\ \bar{X_2}\). Como consecuencia, el error estándar por el que debemos dividir es, de hecho, el error estándar de la diferencia entre medias. Siempre y cuando las dos variables realmente tengan la misma desviación estándar, entonces nuestra estimación para el error estándar es
\(\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)=\hat{\sigma} \sqrt{\dfrac{1}{N_{1}}+\dfrac{1}{N_{2}}}\)
y nuestra estadística t es, por lo tanto
\(t=\dfrac{\bar{X}_{1}-\bar{X}_{2}}{\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)}\)
(impactante, ¿no?) siempre y cuando la hipótesis nula sea cierta, y se cumplan todos los supuestos de la prueba. Los grados de libertad, sin embargo, son ligeramente diferentes. Como es habitual, podemos pensar en los grados de libertad para ser iguales al número de puntos de datos menos el número de restricciones. En este caso, tenemos N observaciones (N1 en la muestra 1 y N2 en la muestra 2) y 2 restricciones (las medias de la muestra). Entonces los grados totales de libertad para esta prueba son N−2.
Haciendo la prueba en R
No es sorprendente que pueda ejecutar una prueba t de muestras independientes usando la función t.test () (Sección 13.7), pero una vez más voy a comenzar con una función algo más simple en el paquete lsr. Esa función se llama inimaginativamente independentSampleTestTest (). Primero, recordemos que nuestros datos se ven así:
head( harpo )## grade tutor
## 1 65 Anastasia
## 2 72 Bernadette
## 3 66 Bernadette
## 4 74 Anastasia
## 5 73 Anastasia
## 6 71 BernadetteLa variable de resultado para nuestra prueba es la calificación del estudiante, y los grupos se definen en términos del tutor para cada clase. Así que probablemente no te sorprenderá demasiado al ver que vamos a describir la prueba que queremos en términos de una fórmula R que se lee como este grado ~ tutor. El comando específico que necesitamos es:
independentSamplesTTest(
formula = grade ~ tutor, # formula specifying outcome and group variables
data = harpo, # data frame that contains the variables
var.equal = TRUE # assume that the two groups have the same variance
)
##
## Student's independent samples t-test
##
## Outcome variable: grade
## Grouping variable: tutor
##
## Descriptive statistics:
## Anastasia Bernadette
## mean 74.533 69.056
## std dev. 8.999 5.775
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: 2.115
## degrees of freedom: 31
## p-value: 0.043
##
## Other information:
## two-sided 95% confidence interval: [0.197, 10.759]
## estimated effect size (Cohen's d): 0.74Los dos primeros argumentos deben ser familiares para usted. La primera es la fórmula que le dice a R qué variables usar y la segunda le dice a R el nombre del marco de datos que almacena esas variables. El tercer argumento no es tan obvio. Al decir var.equal = VERDADERO, lo que realmente estamos haciendo es decirle a R que use la prueba t de muestras independientes de Student. Más sobre esto más adelante. Por ahora, ignoremos ese bit y veamos la salida:
La salida tiene una forma muy familiar. Primero, te dice qué prueba se ejecutó, y te dice los nombres de las variables que usaste. La segunda parte de la salida reporta las medias muestrales y las desviaciones estándar para ambos grupos (es decir, ambos grupos tutoriales). La tercera sección de la salida establece la hipótesis nula y la hipótesis alternativa en una forma bastante explícita. Luego informa los resultados de la prueba: al igual que la última vez, los resultados de la prueba consisten en un estadístico t, los grados de libertad y el valor p. La sección final informa dos cosas: te da un intervalo de confianza y un tamaño de efecto. Hablaré de los tamaños de los efectos más adelante. El intervalo de confianza, sin embargo, debería hablar ahora.
Es muy importante tener claro a qué se refiere realmente este intervalo de confianza: es un intervalo de confianza para la diferencia entre las medias grupales. En nuestro ejemplo, los estudiantes de Anastasia tuvieron una nota promedio de 74.5, y los estudiantes de Bernadette tuvieron una nota promedio de 69.1, por lo que la diferencia entre las dos medias muestrales es 5.4. Pero claro que la diferencia entre medias poblacionales podría ser mayor o menor que esta. El intervalo de confianza reportado por la función IndependentSampleTestTest () te dice que hay un 95% de probabilidad de que la verdadera diferencia entre medias esté entre 0.2 y 10.8.
En cualquier caso, la diferencia entre los dos grupos es significativa (apenas), por lo que podríamos escribir el resultado usando texto como este:
El grado medio en la clase de Anastasia fue de 74.5% (std dev = 9.0), mientras que la media en la clase de Bernadette fue de 69.1% (std dev = 5.8). Una prueba t de muestras independientes de Student mostró que esta diferencia de 5.4% fue significativa (t (31) =2.1, p<.05, IC 95 = [0.2,10.8], d=.74), sugiriendo que se ha producido una diferencia genuina en los resultados de aprendizaje.
Observe que he incluido el intervalo de confianza y el tamaño del efecto en el bloque stat. La gente no siempre hace esto. Como mínimo, esperarías ver la estadística t, los grados de libertad y el valor p. Entonces deberías incluir algo como esto como mínimo: t (31) =2.1, p<.05. Si los estadísticos se salieran con la suya, todos también reportarían el intervalo de confianza y probablemente también la medida del tamaño del efecto, porque son cosas útiles para saber. Pero la vida real no siempre funciona de la manera que los estadísticos quieren que funcione: debes hacer un juicio basado en si crees que ayudará a tus lectores, y (si estás escribiendo un artículo científico) el estándar editorial para la revista en cuestión. Algunas revistas esperan que reportes tamaños de efecto, otras no, dentro de algunas comunidades científicas es una práctica estándar reportar intervalos de confianza, en otras no lo es. Tendrás que averiguar qué espera tu audiencia. Pero, solo en aras de la claridad, si vas a tomar mi clase: mi posición predeterminada es que generalmente vale la pena incluir el tamaño del efecto, pero no te preocupes por el intervalo de confianza a menos que la tarea te lo pida o implique que deberías hacerlo.
Valores t positivos y negativos
Antes de pasar a hablar sobre los supuestos de la prueba t, hay un punto adicional que quiero hacer sobre el uso de las pruebas t en la práctica. El primero se relaciona con el signo del estadístico t (es decir, si se trata de un número positivo o uno negativo). Una preocupación muy común que tienen los estudiantes cuando empiezan a ejecutar su primera prueba t es que a menudo terminan con valores negativos para el estadístico t, y no saben interpretarlo. De hecho, no es nada raro que dos personas que trabajan independientemente terminen con salidas R que son casi idénticas, excepto que una persona tiene valores t negativos y la otra tiene un valor t positivo. Asumiendo que estás ejecutando una prueba a dos caras, entonces los valores p serán idénticos. En una inspección más cercana, los alumnos notarán que los intervalos de confianza también tienen los signos opuestos. Esto está perfectamente bien: siempre que esto suceda, lo que encontrarás es que las dos versiones de la salida R surgen de formas ligeramente diferentes de ejecutar la prueba t. Lo que está pasando aquí es muy sencillo. El estadístico t que R está calculando aquí es siempre de la forma
\(t=\dfrac{(\text { mean } 1)-(\text { mean } 2)}{(\mathrm{SE})}\)
Si “media 1" es mayor que “media 2” el estadístico t será positivo, mientras que si “media 2” es mayor entonces el estadístico t será negativo. De igual manera, el intervalo de confianza que informa R es el intervalo de confianza para la diferencia “(media 1) menos (media 2)”, que será lo contrario de lo que obtendrías si estuvieras calculando el intervalo de confianza para la diferencia “(media 2) menos (media 1)”.
Bien, eso es bastante sencillo cuando lo piensas, pero ahora considera nuestra prueba t comparando la clase de Anastasia con la clase de Bernadette. A cuál deberíamos llamar “media 1” y a cuál deberíamos llamar “media 2”. Es arbitrario. Sin embargo, realmente es necesario designar a uno de ellos como “media 1” y al otro como “media 2”. No en vano, la forma en que R maneja esto también es bastante arbitraria. En versiones anteriores del libro solía tratar de explicarlo, pero después de un tiempo me di por vencido, porque en realidad no es tan importante, y para ser honesto nunca podré recordarme a mí mismo. Siempre que obtengo un resultado significativo de la prueba t, y quiero averiguar cuál media es la más grande, no trato de resolverlo mirando la estadística t. ¿Por qué me molestaría en hacer eso? Es una tontería. Es más fácil solo mirar los medios reales del grupo, ya que la salida R realmente los muestra!
Aquí está lo importante. Porque realmente no importa lo que R imprimiera, normalmente trato de reportar la estadística t de tal manera que los números coincidan con el texto. Esto es lo que quiero decir... supongamos que lo que quiero escribir en mi informe es “La clase de Anastasia tuvo calificaciones más altas que la clase de Bernadette”. El fraseo aquí implica que el grupo de Anastasia es lo primero, por lo que tiene sentido reportar la estadística t como si la clase de Anastasia correspondiera al grupo 1. Si es así, escribiría
La clase de Anastasia tuvo calificaciones superiores a la de Bernadette (t (31) =2.1, p=.04).
(En realidad no enfatizaría la palabra “superior” en la vida real, solo lo estoy haciendo para hacer hincapié en el punto de que “superior” corresponde a valores t positivos). Por otro lado, supongamos que el fraseo que quería usar tiene la clase de Bernadette listada primero. Si es así, tiene más sentido tratar a su clase como el grupo 1, y si es así, la redacción se ve así:
La clase de Bernadette tuvo calificaciones más bajas que la clase de Anastasia (t (31) =−2.1, p=.04).
Debido a que estoy hablando de un grupo que tiene puntuaciones “más bajas” en esta ocasión, es más sensato usar la forma negativa del estadístico t. Simplemente hace que se lea más limpiamente.
Una última cosa: tenga en cuenta que no puede hacer esto para otros tipos de estadísticas de prueba. Funciona para pruebas t, pero no sería significativo para las pruebas F de chi-cuadrado o, de hecho, para la mayoría de las pruebas de las que hablo en este libro. ¡Así que no sobregeneralice este consejo! ¡De verdad solo estoy hablando de pruebas t aquí y nada más!
Supuestos de la prueba
Como siempre, nuestra prueba de hipótesis se basa en algunas suposiciones. Entonces, ¿qué son? Para la prueba t de Student existen tres supuestos, algunos de los cuales vimos previamente en el contexto de la prueba t de una muestra (ver Sección 13.2.3):
- Normalidad. Al igual que la prueba t de una muestra, se supone que los datos se distribuyen normalmente. Específicamente, asumimos que ambos grupos están normalmente distribuidos. En la Sección 13.9 discutiremos cómo probar la normalidad, y en la Sección 13.10 discutiremos posibles soluciones.
- Independencia. Una vez más, se asume que las observaciones son muestreadas de forma independiente. En el contexto de la prueba de Student esto tiene dos aspectos a la misma. En primer lugar, asumimos que las observaciones dentro de cada muestra son independientes entre sí (exactamente las mismas que para la prueba de una muestra). Sin embargo, también asumimos que no hay dependencias entre muestras. Si, por ejemplo, resulta que incluyste a algunos participantes en ambas condiciones experimentales de tu estudio (por ejemplo, al permitir accidentalmente que la misma persona se inscriba en diferentes condiciones), entonces hay algunas dependencias de muestra cruzada que deberías tener en cuenta.
- Homogeneidad de varianza (también llamada “homocedasticidad”). El tercer supuesto es que la desviación estándar poblacional es la misma en ambos grupos. Puedes probar esta suposición usando la prueba Levene, de la que hablaré más adelante en el libro (Sección 14.7). No obstante, hay un remedio muy sencillo para esta suposición, del que hablaré en la siguiente sección.


