13.4: La prueba t de muestras independientes (prueba de Welch)
- Page ID
- 151788
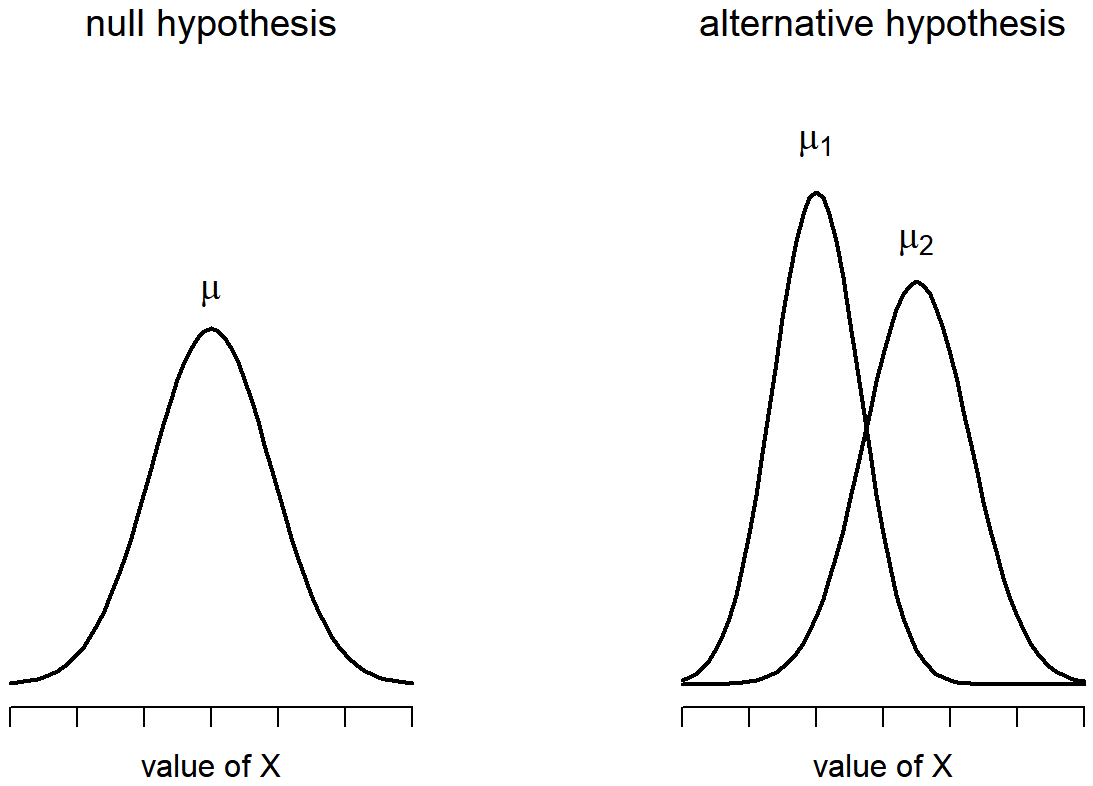
El mayor problema con el uso de la prueba de Student en la práctica es el tercer supuesto enumerado en el apartado anterior: asume que ambos grupos tienen la misma desviación estándar. Esto rara vez es cierto en la vida real: si dos muestras no tienen los mismos medios, ¿por qué deberíamos esperar que tengan la misma desviación estándar? Realmente no hay razón para esperar que esta suposición sea cierta. Hablaremos un poco sobre cómo puedes verificar esta suposición más adelante porque sí surge en algunos lugares diferentes, no solo en la prueba t. Pero ahora mismo voy a hablar de una forma diferente de la prueba t (Welch 1947) que no se basa en esta suposición. En la Figura 13.10 se muestra una ilustración gráfica de lo que supone la prueba t de Welch sobre los datos, para proporcionar un contraste con la versión de la prueba de Student en la Figura 13.9. Admito que es un poco extraño hablar de la cura antes de hablar del diagnóstico, pero como sucede la prueba de Welch es la prueba t predeterminada en R, así que este es probablemente el mejor lugar para discutirlo.
La prueba de Welch es muy similar a la prueba de Student. Por ejemplo, el estadístico t que utilizamos en la prueba de Welch se calcula de la misma manera que lo es para la prueba de Student. Es decir, tomamos la diferencia entre las medias de la muestra, y luego la dividimos por alguna estimación del error estándar de esa diferencia:
\(t=\dfrac{\bar{X}_{1}-\bar{X}_{2}}{\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)}\)
La principal diferencia es que los cálculos de error estándar son diferentes. Si las dos poblaciones tienen diferentes desviaciones estándar, entonces es una completa tontería tratar de calcular una estimación de desviación estándar agrupada, porque estás promediando manzanas y naranjas. 193 Pero aún se puede estimar el error estándar de la diferencia entre medias de muestra; simplemente termina luciendo diferente:
\(\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)=\sqrt{\dfrac{\hat{\sigma}_{1}^{2}}{N_{1}}+\dfrac{\hat{\sigma}_{2}^{2}}{N_{2}}}\)
La razón por la que se calcula de esta manera está más allá del alcance de este libro. Lo que importa para nuestros propósitos es que la estadística t que sale de la prueba de Welch es en realidad algo diferente a la que viene de la prueba de Student.
La segunda diferencia entre Welch y Student es que los grados de libertad se calculan de una manera muy diferente. En la prueba de Welch, los “grados de libertad” ya no tienen que ser un número entero, y no corresponde tanto a la heurística de “número de puntos de datos menos el número de restricciones” que he estado usando hasta este punto. Los grados de libertad son, de hecho...
\(\mathrm{d} \mathrm{f}=\dfrac{\left(\hat{\sigma}_{1}^{2} / N_{1}+\hat{\sigma}_{2}^{2} / N_{2}\right)^{2}}{\left(\hat{\sigma}_{1}^{2} / N_{1}\right)^{2} /\left(N_{1}-1\right)+\left(\hat{\sigma}_{2}^{2} / N_{2}\right)^{2} /\left(N_{2}-1\right)}\)
... lo cual es todo bastante sencillo y obvio, ¿verdad? Bueno, tal vez no. Realmente no importa para fines fuera. Lo que importa es que verás que el valor “df” que sale de una prueba de Welch tiende a ser un poco más pequeño que el usado para la prueba de Student, y no tiene que ser un número entero.
Haciendo la prueba en R
Ejecutar una prueba de Welch en R es bastante fácil. Todo lo que tienes que hacer es no molestarte en decirle a R que asuma varianzas iguales. Es decir, tomas el comando que usamos para ejecutar una prueba t de Student y bajas el bit var.equal = VERDADERO. Entonces el comando para una prueba de Welch se convierte en:
independentSamplesTTest(
formula = grade ~ tutor, # formula specifying outcome and group variables
data = harpo # data frame that contains the variables
)##
## Welch's independent samples t-test
##
## Outcome variable: grade
## Grouping variable: tutor
##
## Descriptive statistics:
## Anastasia Bernadette
## mean 74.533 69.056
## std dev. 8.999 5.775
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: 2.034
## degrees of freedom: 23.025
## p-value: 0.054
##
## Other information:
## two-sided 95% confidence interval: [-0.092, 11.048]
## estimated effect size (Cohen's d): 0.724No demasiado difícil, ¿verdad? No es sorprendente que la salida tenga exactamente el mismo formato que la última vez también:
La primera línea es diferente, porque te está diciendo que es ejecutar una prueba de Welch en lugar de una prueba de Student, y por supuesto todos los números son un poco diferentes. Pero espero que la interpretación de este resultado sea bastante obvia. Lees el resultado de la misma manera que lo harías para la prueba de Student. Tienes tus estadísticas descriptivas, las hipótesis, los resultados de las pruebas y alguna otra información. Así que todo eso es bastante fácil.
Excepto, excepto... nuestro resultado ya no es significativo. Cuando ejecutamos la prueba de Student, sí obtuvimos un efecto significativo; pero la prueba de Welch en el mismo conjunto de datos no es (t (23.03) =2.03, p=.054). ¿Qué significa esto? ¿Deberíamos entrar en pánico? ¿Está ardiendo el cielo? Probablemente no. El hecho de que una prueba sea significativa y la otra no lo sea en sí mismo no significa mucho, sobre todo porque como que amañé los datos para que esto sucediera. Como regla general, no es buena idea hacer todo lo posible para intentar interpretar o explicar la diferencia entre un valor p de .049 y un valor p de .051. Si este tipo de cosas suceden en la vida real, la diferencia en estos valores p es casi seguro que se debe al azar. Lo que sí importa es que te cuides un poco al pensar en qué prueba usas. La prueba de Student y la prueba de Welch tienen diferentes fortalezas y debilidades. Si las dos poblaciones realmente tienen varianzas iguales, entonces la prueba de Student es ligeramente más potente (menor tasa de error Tipo II) que la prueba de Welch. No obstante, si no tienen las mismas varianzas, entonces se violan los supuestos de la prueba de Student y es posible que no puedas confiar en ella: podrías terminar con una tasa de error de Tipo I más alta. Entonces es un intercambio. Sin embargo, en la vida real, tiendo a preferir la prueba de Welch; porque casi nadie cree realmente que las varianzas poblacionales sean idénticas.
Supuestos de la prueba
Los supuestos de la prueba de Welch son muy similares a los realizados por la prueba t de Student (ver Sección 13.3.8), excepto que la prueba de Welch no asume homogeneidad de varianza. Esto deja sólo el supuesto de normalidad, y el supuesto de independencia. Los detalles de estos supuestos son los mismos para la prueba de Welch que para la prueba de Student.


