6.1: Efectos principales y efecto de interacción

En el capítulo anterior se utilizó ANOVA unidireccional para analizar datos de tres o más poblaciones utilizando la hipótesis nula de que todas las medias eran iguales (sin efecto de tratamiento). Por ejemplo, un biólogo quiere comparar el crecimiento medio para tres niveles diferentes de fertilizante. Un ANOVA unidireccional prueba para ver si al menos uno de los medios de tratamiento es significativamente diferente de los demás. Si se rechaza la hipótesis nula, se puede usar un método de comparación múltiple, como el de Tukey, para identificar qué medias son diferentes, y el intervalo de confianza se puede usar para estimar la diferencia entre las diferentes medias.

Supongamos que el biólogo quiere hacer esta misma pregunta pero con dos especies diferentes de plantas mientras sigue probando los tres diferentes niveles de fertilizante. El biólogo necesita investigar no solo el crecimiento promedio entre las dos especies (efecto principal A) y el crecimiento promedio para los tres niveles de fertilizante (efecto principal B), sino también la interacción o relación entre los dos factores de especie y fertilizante. El análisis bidireccional de varianza permite al biólogo responder a la pregunta sobre el crecimiento afectado por especies y niveles de fertilizante, y dar cuenta de la variación debida a ambos factores simultáneamente.

Nuestro examen de ANOVA de una vía se realizó en el contexto de un diseño completamente al azar donde los tratamientos se asignan aleatoriamente a cada sujeto (o unidad experimental). Ahora consideramos el análisis en el que dos factores pueden explicar la variabilidad en la variable respuesta. Recuerde que podemos tratar los factores controlándolos, fijándolos en niveles específicos, y aplicando aleatoriamente los tratamientos para minimizar el efecto de las variables incontroladas sobre la variable de respuesta. Con dos factores, necesitamos un experimento factorial.

Cuadro 1. Datos observados para dos especies en tres niveles de fertilizante.

Este es un ejemplo de un experimento factorial en el que hay un total de 2 x 3 = 6 posibles combinaciones de los niveles para los dos factores diferentes (especie y nivel de fertilizante). Estas seis combinaciones se denominan tratamientos y el experimento se denomina experimento factorial de 2 x 3. Utilizamos este tipo de experimentos para investigar el efecto de múltiples factores en una respuesta y la interacción entre los factores. Cada una de las n observaciones de la variable de respuesta para los diferentes niveles de los factores existe dentro de una celda. En este ejemplo, hay seis células y cada célula corresponde a un tratamiento específico.

Al comparar las medias de tratamiento para un experimento factorial (o para cualquier otro experimento), se requieren múltiples observaciones para cada tratamiento. A estos se les llama réplicas. Por ejemplo, si tienes cuatro observaciones para cada uno de los seis tratamientos, tienes cuatro repeticiones del experimento. La replicación demuestra que los resultados son reproducibles y proporciona los medios para estimar la varianza de error experimental. La replicación también proporciona la capacidad de aumentar la precisión para las estimaciones de los medios de tratamiento. El aumento de la replicación disminuye\(s_{\frac{2}{y}} = \frac {s^2}{r}\) aumentando así la precisión de\(\bar y\).

Notación

• k = número de niveles de factor A
• l = número de niveles de factor B
• kl = número de tratamientos (cada uno una combinación de un nivel de factor A y un nivel de factor B)
• m = número de observaciones en cada tratamiento

Efectos principales y efecto de interacción

Los efectos principales tratan cada factor por separado. En el ejemplo anterior tenemos dos factores, A y B. El principal efecto del Factor A (especie) es la diferencia entre el crecimiento medio para la Especie 1 y la Especie 2, promediado a través de los tres niveles de fertilizante. El efecto principal del Factor B (fertilizante) es la diferencia en el crecimiento promedio para los niveles 1, 2 y 3 promediados entre las dos especies. La interacción son los cambios simultáneos en los niveles de ambos factores. Si los cambios en el nivel del Factor A resultan en diferentes cambios en el valor de la variable de respuesta para los diferentes niveles del Factor B, decimos que existe un efecto de interacción entre los factores. Considera el siguiente ejemplo para ayudar a aclarar esta idea de interacción.

Ejemplo\(\PageIndex{1}\):

El Factor A tiene dos niveles y el Factor B tiene dos niveles. En el cuadro izquierdo, cuando el Factor A está en el nivel 1, el Factor B cambia en 3 unidades. Cuando el Factor A está en el nivel 2, el Factor B vuelve a cambiar en 3 unidades. De igual manera, cuando el Factor B está en el nivel 1, el Factor A cambia en 2 unidades. Cuando el Factor B está en el nivel 2, el Factor A vuelve a cambiar en 2 unidades. No hay interacción. El cambio en la respuesta promedio real cuando el nivel de cualquiera de los factores cambia de 1 a 2 es el mismo para cada nivel del otro factor. En este caso, los cambios en los niveles de los dos factores afectan la respuesta promedio verdadera por separado, o de manera aditiva.

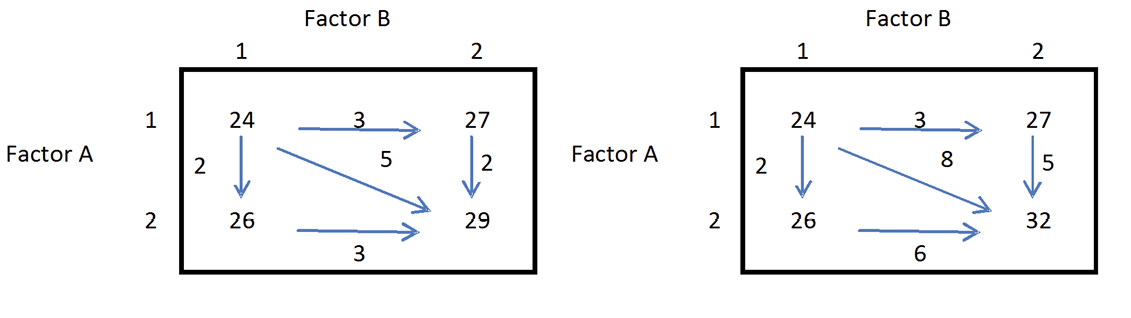
Figura 1. Ilustración del efecto de interacción.

Solución

La caja derecha ilustra la idea de interacción. Cuando el Factor A está en el nivel 1, el Factor B cambia en 3 unidades pero cuando el Factor A está en el nivel 2, el Factor B cambia en 6 unidades. Cuando el Factor B está en el nivel 1, el Factor A cambia en 2 unidades pero cuando el Factor B está en el nivel 2, el Factor A cambia en 5 unidades. El cambio en la respuesta promedio real cuando los niveles de ambos factores cambian simultáneamente del nivel 1 al nivel 2 es de 8 unidades, lo que es mucho mayor de lo que sugieren los cambios separados. En este caso, existe una interacción entre los dos factores, por lo que el efecto de los cambios simultáneos no se puede determinar a partir de los efectos individuales de los cambios separados. Cambio en la respuesta promedio real cuando el nivel de un factor cambia depende del nivel del otro factor. No se puede determinar el efecto separado del Factor A o del Factor B en la respuesta debido a la interacción.

Supuestos

Nota: Asunción básica

Las observaciones sobre cualquier tratamiento en particular se seleccionan independientemente de una distribución normal con varianza σ2 (la misma varianza para cada tratamiento), y las muestras de diferentes tratamientos son independientes entre sí.

Podemos utilizar gráficas de probabilidad normal para satisfacer el supuesto de normalidad para cada tratamiento. El requisito de varianzas iguales es más difícil de confirmar, pero generalmente podemos verificar asegurándonos de que la desviación estándar de la muestra más grande no sea más del doble de la desviación estándar de la muestra más pequeña.

Aunque no es un requisito para ANOVA de dos vías, tener un número igual de observaciones en cada tratamiento, denominado diseño de equilibrio, aumenta la potencia de la prueba. Sin embargo, las repeticiones desiguales (un diseño desequilibrado), son muy comunes. Algunos paquetes de software estadístico (como Excel) solo funcionarán con diseños equilibrados. Minitab proporcionará el análisis correcto para diseños balanceados y desequilibrados en el componente Modelo Lineal General bajo análisis estadístico ANOVA. No obstante, en aras de la simplicidad, nos centraremos en diseños equilibrados en este capítulo.

Sumas de Cuadrados y Tabla ANOVA

En el capítulo anterior, se introdujo la idea de sumas de cuadrados para dividir la variación por tratamiento y variación aleatoria. La relación es la siguiente:

\[SSTo = SSTr + SSE\]

Ahora particionamos la variación aún más para reflejar los efectos principales (Factor A y Factor B) y el término de interacción:

\[SSTo = SSA + SSB +SSAB +SSE\]

donde

1. SsTo es la suma total de cuadrados, con los grados asociados de libertad klm — 1
2. SSA es el factor A principal efecto sumas de cuadrados, con grados asociados de libertad k — 1
3. SSB es el factor B principal efecto sumas de cuadrados, con grados asociados de libertad l — 1
4. SSAB es la suma de interacción de cuadrados, con grados de libertad asociados (k — 1) (l — 1)
5. SSE es la suma del error de cuadrados, con grados de libertad asociados kl (m — 1)

Como vimos en el capítulo anterior, la magnitud de la SSE está completamente relacionada con la cantidad de variabilidad subyacente en las distribuciones que se muestrean. No tiene nada que ver con los valores de las diversas respuestas medias verdaderas. SSAB refleja en parte la variabilidad subyacente, pero su valor también se ve afectado por si existe o no una interacción entre los factores; cuanto mayor sea la interacción, mayor será el valor de SSAB.

La siguiente tabla ANOVA ilustra la relación entre las sumas de cuadrados para cada componente y el estadístico F resultante para probar las tres hipótesis nulas y alternativas para un ANOVA bidireccional.

1. \(H_0\): No hay interacción entre factores
   \(H_1\): Hay una interacción significativa entre factores
2. \(H_0\): No hay efecto del Factor A sobre la variable de respuesta
   \(H_1\): Hay un efecto del Factor A en la variable de respuesta
3. \(H_0\): No hay efecto del Factor B sobre la variable de respuesta
   \(H_1\): Hay un efecto del Factor B en la variable de respuesta

Si hay una interacción significativa, entonces ignore los siguientes dos conjuntos de hipótesis para los efectos principales. Una interacción significativa te dice que el cambio en la verdadera respuesta promedio para un nivel de Factor A depende del nivel de Factor B. El efecto de los cambios simultáneos no se puede determinar examinando los efectos principales por separado. Si NO hay una interacción significativa, entonces proceda a probar los efectos principales. Las sumas de cuadrados del Factor A reflejarán la variación aleatoria y cualquier diferencia entre las respuestas promedio verdaderas para diferentes niveles del Factor A. De manera similar, las sumas de cuadrados del Factor B reflejarán la variación aleatoria y las respuestas promedio verdaderas para los diferentes niveles del Factor B.

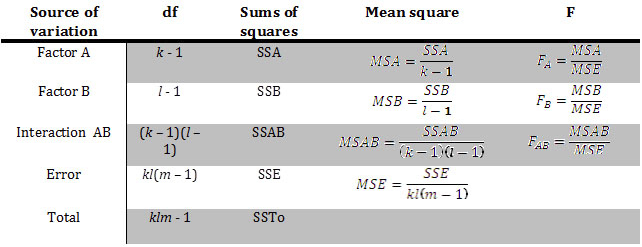
Cuadro 2. Tabla ANOVA de dos vías.

Cada una de las cinco fuentes de variación, cuando se divide por los grados de libertad apropiados (df), proporciona una estimación de la variación en el experimento. Las estimaciones se denominan cuadrados medios y se muestran junto con sus respectivas sumas de cuadrados y df en la tabla de análisis de varianza. En ANOVA unidireccional, el error cuadrático medio (MSE) es la mejor estimación de\(\sigma^2\) (la varianza poblacional) y es el denominador en el estadístico F. En un ANOVA bidireccional, sigue siendo la mejor estimación de\(\sigma^2\). Observe que en cada caso, el MSE es el denominador en el estadístico de prueba y el numerador es la suma media de cuadrados para cada factor principal y término de interacción. El estadístico F se encuentra en la columna final de esta tabla y se utiliza para responder a las tres hipótesis alternativas. Por lo general, los valores p asociados a cada estadístico F también se presentan en una tabla ANOVA. Utilizarás la Regla de Decisión para determinar el resultado de cada uno de los tres pares de hipótesis.

Si el valor p es menor que α (nivel de significancia), rechazará la hipótesis nula.

Cuando realizamos un ANOVA bidireccional, siempre probamos primero la hipótesis con respecto al efecto de interacción. Si se rechaza la hipótesis nula de no interacción, NO interpretamos los resultados de las hipótesis que involucran los efectos principales. Si el término de interacción NO es significativo, entonces examinamos los dos efectos principales por separado. Veamos un ejemplo.

Ejemplo\(\PageIndex{2}\):

Se realizó un experimento para evaluar los efectos de la variedad de plantas de soya (factor A, con k = 3 niveles) y la densidad de siembra (factor B, con l = 4 niveles — 5, 10, 15 y 20 mil plantas por hectárea) sobre el rendimiento. Cada uno de los 12 tratamientos (k * l) se aplicó aleatoriamente a m = 3 parcelas (klm = 36 observaciones totales). Utilice un ANOVA bidireccional para evaluar los efectos a un nivel de significancia del 5%.

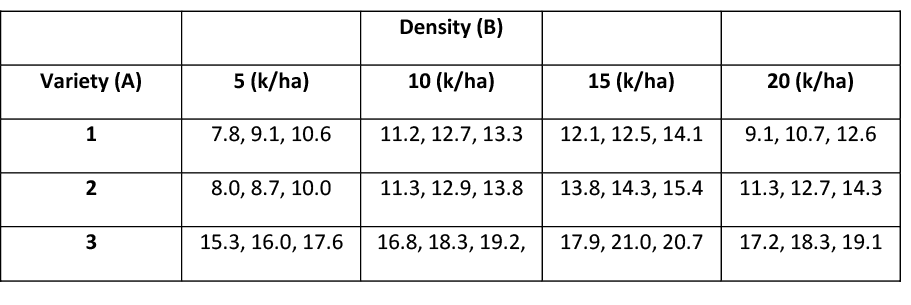
Cuadro 3. Datos observados para tres variedades de plantas de soya a cuatro densidades.

Siempre es importante observar los rendimientos promedio de la muestra para cada tratamiento, cada nivel de factor A y cada nivel de factor B.

Cuadro 4. Tabla de resumen.

	Densidad
Variedad	5	10	15	20	Rendimiento promedio de la muestra para cada nivel de factor A
1	9.17	12.40	12.90	10.80	11.32
2	8.90	12.67	14.50	12.77	12.21
3	16.30	18.10	19.87	18.20	18.12
Rendimiento promedio de la muestra para cada nivel de factor B	11.46	14.39	15.77	13.92	13.88

Por ejemplo, 11.32 es el rendimiento promedio para la variedad #1 sobre todos los niveles de densidades de siembra. El valor 11.46 es el rendimiento promedio para parcelas sembradas con 5,000 plantas en todas las variedades. La gran media es 13.88. A continuación se presenta la tabla ANOVA.

Cuadro 5. Tabla ANOVA de dos vías.

Fuente	DF	SS	MSS	F	P
variedad	2	327.774	163.887	100.48	<0.001
densidad	3	86.908	28.969	17.76	<0.001
variedad*densidad	6	8.068	1.345	0.82	0.562
error	24	39.147	1.631
total	35

Se inicia con las siguientes hipótesis nulas y alternativas:

• \(H_0\): No hay interacción entre factores
• \(H_1\): Hay una interacción significativa entre los factores

El estadístico F:

\[F_{AB} = \dfrac {MSAB}{MSE} = \dfrac {1.345}{1.631} = 0.82\]

El valor p para la prueba para una interacción significativa entre factores es 0.562. Este valor p es mayor al 5% (α), por lo tanto fallamos en rechazar la hipótesis nula. No hay evidencia de una interacción significativa entre variedad y densidad. Por lo que es conveniente realizar más pruebas respecto a la presencia de los efectos principales.

\(H_0\): No hay efecto del Factor A (variedad) sobre la variable de respuesta

\(H_1\): Hay un efecto del Factor A en la variable de respuesta

El estadístico F:

\[F_{A} = \dfrac {MSA}{MSE} = \dfrac {163.887}{1.631} = 100.48\]

El valor p (<0.001) es menor que 0.05 por lo que rechazaremos la hipótesis nula. Existe una diferencia significativa en el rendimiento entre las tres variedades.

• \(H_0\): No hay efecto del Factor B (densidad) sobre la variable de respuesta
• \(H_1\): Hay un efecto del Factor B en la variable de respuesta

El estadístico F:

\[F_A = \dfrac {MSB}{MSE} = \dfrac {28.969}{1.631} = 17.76\]

El valor p (<0.001) es menor que 0.05 por lo que rechazaremos la hipótesis nula. Hay una diferencia significativa en el rendimiento entre las cuatro densidades de siembra.