3.3: Error estándar de la media

Objetivos de aprendizaje

• El error estándar de la media te indica qué tan precisa es probable que sea tu estimación de la media.

Introducción

Cuando tomas una muestra de observaciones de una población y calculas la media muestral, estás estimando la media paramétrica, o media de todos los individuos de la población. Tu media de muestra no será exactamente igual a la media paramétrica que intentas estimar, y te gustaría tener una idea de lo cerca que es probable que esté la media de tu muestra. Si el tamaño de su muestra es pequeño, su estimación de la media no será tan buena como una estimación basada en un tamaño de muestra más grande. Aquí hay muestras\(10\) aleatorias de un conjunto de datos simulados con una media verdadera (paramétrica) de\(5\). Los\(X's\) representan las observaciones individuales, los círculos rojos son las medias de la muestra y la línea azul es la media paramétrica.

Fig. 3.3.1 Observaciones individuales (X's) y medias (puntos rojos) para muestras aleatorias de una población con una media paramétrica de 5 (línea horizontal).

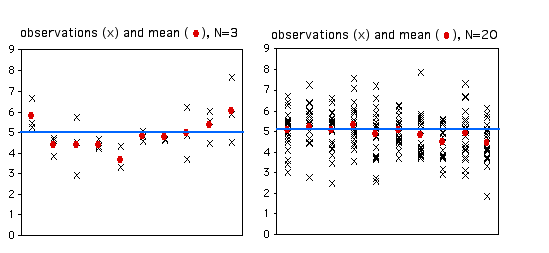
Como puede ver, con un tamaño de muestra de solo\(3\), algunas de las medias de la muestra no están muy cerca de la media paramétrica. La primera muestra resultó ser tres observaciones que fueron todas mayores que\(5\), por lo que la media de la muestra es demasiado alta. La segunda muestra tiene tres observaciones que fueron menores que\(5\), por lo que la media de la muestra es demasiado baja. Con\(20\) observaciones por muestra, las medias de la muestra son generalmente más cercanas a la media paramétrica.

Una vez que hayas calculado la media de una muestra, debes informar a las personas qué tan cerca es probable que esté la media de la muestra a la media paramétrica. Una forma de hacerlo es con el error estándar de la media. Si se toman muchas muestras aleatorias de una población, el error estándar de la media es la desviación estándar de las diferentes medias de la muestra. Alrededor de dos tercios (\(68.3\%\)) de las medias de la muestra estarían dentro de un error estándar de la media paramétrica,\(95.4\%\) estarían dentro de dos errores estándar, y casi todos (\(99.7\%\)) estarían dentro de tres errores estándar.

Fig. 3.3.2 Medias de 100 muestras aleatorias (N=3) de una población con una media paramétrica de 5 (línea horizontal).

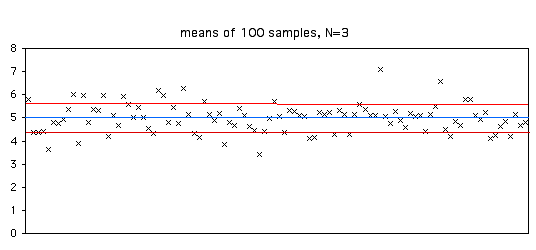
Aquí hay una figura que ilustra esto. Tomé\(100\) muestras\(3\) de una población con una media paramétrica de\(5\) (mostrada por la línea azul). La desviación estándar de las\(100\) medias fue\(0.63\). De las medias de la\(100\) muestra,\(70\) están entre\(4.37\) y\(5.63\) (la media paramétrica\(\pm\) un error estándar).

Por lo general, no tendrá múltiples muestras para usar en la realización de múltiples estimaciones de la media. Afortunadamente, se puede estimar el error estándar de la media utilizando el tamaño de la muestra y la desviación estándar de una sola muestra de observaciones. El error estándar de la media se estima por la desviación estándar de las observaciones dividida por la raíz cuadrada del tamaño de la muestra. Por alguna razón, no hay ninguna función de hoja de cálculo para el error estándar, por lo que puedes usar =STDEV (Ys) /SQRT (COUNT (Ys)), donde\(Ys\) está el rango de celdas que contienen tus datos.

Esta cifra es la misma que la anterior, solo que esta vez he añadido barras de error que indican error\(\pm 1\) estándar. Debido a que la estimación del error estándar se basa en solo tres observaciones, varía mucho de una muestra a otra.

Fig. 3.3.3 Medias ±1 error estándar de 100 muestras aleatorias (n=3) de una población con una media paramétrica de 5 (línea horizontal).

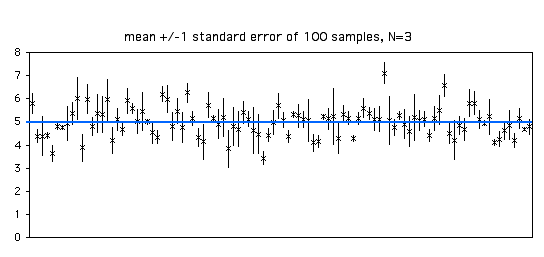
Con un tamaño de muestra de\(20\), cada estimación del error estándar es más precisa. De las\(100\) muestras en la gráfica siguiente,\(68\) incluir la media paramétrica dentro del error\(\pm 1\) estándar de la media muestral.

Fig. 3.3.4 Medias ±1 error estándar de 100 muestras aleatorias (N=20) de una población con una media paramétrica de 5 (línea horizontal).

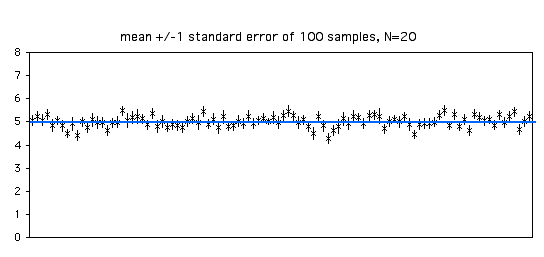
A medida que aumente el tamaño de su muestra, el error estándar de la media se hará más pequeño. Con tamaños de muestra más grandes, la media muestral se convierte en una estimación más precisa de la media paramétrica, por lo que el error estándar de la media se vuelve más pequeño. Tenga en cuenta que es una función de la raíz cuadrada del tamaño de la muestra; por ejemplo, para que el error estándar sea la mitad de grande, necesitará cuatro veces más observaciones.

“Error estándar de la media” y “desviación estándar de la media” son términos equivalentes. La gente casi siempre dice “error estándar de la media” para evitar confusiones con la desviación estándar de las observaciones. En ocasiones el “error estándar” se usa por sí mismo; esto casi con certeza indica el error estándar de la media, pero debido a que también hay estadísticas para error estándar de la varianza, error estándar de la mediana, error estándar de un coeficiente de regresión, etc., se debe especificar el error estándar de la media.

Existe el mito de que cuando dos medios tienen barras de error estándar que no se superponen, las medias son significativamente diferentes (a\(P<0.05\) nivel). Esto no es cierto (Browne 1979, Payton et al. 2003); es fácil que dos conjuntos de números tengan barras de error estándar que no se superpongan, pero no sean significativamente diferentes mediante una prueba t de dos muestras. No intentes hacer pruebas estadísticas comparando visualmente las barras de error estándar, solo usa la prueba estadística correcta.

Estadísticas similares

Los intervalos de confianza y el error estándar de la media tienen el mismo propósito, para expresar la confiabilidad de una estimación de la media. Cuando miras artículos científicos, a veces las “barras de error” en las gráficas o el\(\pm\) número tras medias en tablas representan el error estándar de la media, mientras que en otros artículos representan intervalos de\(95\%\) confianza. Prefiero intervalos de\(95\%\) confianza. Cuando veo una gráfica con un montón de puntos y barras de error que representan medias e intervalos de confianza, sé que la mayoría (\(95\%\)) de las barras de error incluyen las medias paramétricas. Cuando las barras de error son errores estándar de la media, solo se espera que alrededor de dos tercios de las barras de error incluyan las medias paramétricas; tengo que duplicar mentalmente las barras para obtener el tamaño aproximado del intervalo de\(95\%\) confianza. Además, para tamaños de muestra muy pequeños, el intervalo de\(95\%\) confianza es mayor que el doble del error estándar, y el factor de corrección es aún más difícil de hacer en tu cabeza. Cualquiera que sea la estadística que decida usar, asegúrese de dejar claro qué representan las barras de error en sus gráficas. He visto muchos gráficos en revistas científicas que no dieron idea de lo que representan las barras de error, lo que las hace bastante inútiles.

Utiliza la desviación estándar y el coeficiente de variación para mostrar cuánta variación hay entre las observaciones individuales, mientras que usas el error estándar o intervalos de confianza para mostrar qué tan buena es tu estimación de la media. La única vez que reportarías desviación estándar o coeficiente de variación sería si realmente estás interesado en la cantidad de variación. Por ejemplo, si cultivaste un montón de plantas de soya con dos tipos diferentes de fertilizantes, tu principal interés probablemente sería si el rendimiento de la soja era diferente, por lo que reportarías el rendimiento medio ± ya sea error estándar o intervalos de confianza. Si ibas a hacer selección artificial en la soja para reproducirse para un mejor rendimiento, te podría interesar qué tratamiento tuvo la mayor variación (facilitando la selección de la soja de más rápido crecimiento), así entonces reportarías la desviación estándar o coeficiente de variación.

No tiene sentido reportar tanto el error estándar de la media como la desviación estándar. Siempre y cuando reporte uno de ellos, más el tamaño de la muestra (\(N\)), cualquiera que necesite puede calcular el otro.

Ejemplo

El error estándar de la media para los datos de dace de nariz negra de la página web de tendencia central es\(10.70\).

Cómo calcular el error estándar

Hoja de Cálculo

La hoja de cálculo de estadística descriptiva descriptive.xls calcula el error estándar de la media para hasta\(1000\) observaciones, utilizando la función =STDEV (Ys) /SQRT (COUNT (Ys)).

Páginas web

Esta página web calcula el error estándar de la media y otras estadísticas descriptivas para hasta\(10,000\) observaciones.

Esta página web calcula el error estándar de la media, junto con otras estadísticas descriptivas. No sé el número máximo de observaciones que puede manejar.

R

El\(R\) compañero de Salvatore Mangiafico tiene un programa R de muestra para el error estándar de la media.

SAS

PROC UNIVARIATE calculará el error estándar de la media. Para ejemplos, consulte la página web de tendencia central.

Referencias

1. Browne, R. H. 1979. Sobre la evaluación visual de la significancia de una diferencia de medias. Biometría 35:657-665.
2. Payton, M. E., M. H. Greenstone, y N. Schenker. 2003. Intervalos de confianza superpuestos o intervalos de error estándar: ¿qué significan en términos de significancia estadística? Revista de Ciencia de Insectos 3:34.