3.4: Límites de confianza
- Page ID
- 149216
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Los límites de confianza le indican qué tan precisa es probable que sea su estimación de la media.
Introducción
Después de haber calculado la media de un conjunto de observaciones, debe dar alguna indicación de lo cerca que es probable que esté su estimación a la media paramétrica (“verdadera”). Una forma de hacerlo es con límites de confianza. Los límites de confianza son los números en el extremo superior e inferior de un intervalo de confianza; por ejemplo, si su media es\(7.4\) con límites de confianza de\(5.4\) y\(9.4\), su intervalo de confianza es\(5.4\) a\(9.4\). La mayoría de la gente usa límites de\(95\%\) confianza, aunque podrías usar otros valores. Establecer límites de\(95\%\) confianza significa que si tomaste muestras aleatorias repetidas de una población y calculaste los límites de media y confianza para cada muestra, el intervalo de confianza para\(95\%\) de tus muestras incluiría la media paramétrica.
Para ilustrar esto, aquí están las medias e intervalos de confianza para\(100\) muestras de\(3\) observaciones de una población con una media paramétrica de\(5\). De las\(100\) muestras,\(94\) (mostradas con\(X\) para la media y una línea delgada para el intervalo de confianza) tienen la media paramétrica dentro de su intervalo de\(95\%\) confianza, y\(6\) (mostradas con círculos y líneas gruesas) tienen la media paramétrica fuera del intervalo de confianza.
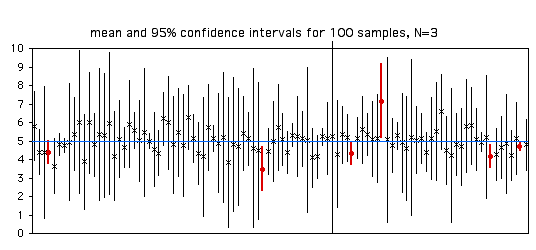
Con tamaños de muestra más grandes, los intervalos de\(95\%\) confianza se hacen más pequeños:

Cuando se calcula el intervalo de confianza para una sola muestra, es tentador decir que “existe la\(95\%\) probabilidad de que el intervalo de confianza incluya la media paramétrica”. Esto es técnicamente incorrecto, porque implica que si recolectas muestras con el mismo intervalo de confianza, a veces incluirían la media paramétrica y otras no lo harían. Por ejemplo, la primera muestra de la figura anterior tiene límites de confianza de\(4.59\) y\(5.51\). Sería incorrecto decir que\(95\%\) de la época, la media paramétrica para esta población estaría entre\(4.59\) y\(5.51\). Si tomaste muestras repetidas de esta misma población y repetidamente obtuviste límites de confianza de\(4.59\) y\(5.51\), la media paramétrica (es decir\(5\), recuerda) estaría en este intervalo\(100\%\) del tiempo. A algunos estadísticos no les importa esta distinción confusa y pedante, pero otros son muy exigentes al respecto, así que es bueno saberlo.
Límites de confianza para las variables de medición
Para calcular los límites de confianza para una variable de medición, multiplique el error estándar de la media por el valor t apropiado. El\(t\) -valor está determinado por la probabilidad (\(0.05\)para un intervalo de\(95\%\) confianza) y los grados de libertad (\(n-1\)). En una hoja de cálculo, podrías usar =( STDEV (Ys) /SQRT (COUNT (Ys))) *TINV (0.05, COUNT (Ys) -1), donde\(Ys\) está el rango de celdas que contienen tus datos. Agrega este valor y lo restas de la media para obtener los límites de confianza. Así, si la media es\(87\) y el\(t\) -valor por el error estándar es\(10.3\), los límites de confianza serían\(76.7\) y\(97.3\). También podría reportar esto como "\(87\pm 10.3\)(límites de\(95\%\) confianza)”. Las personas reportan tanto los límites de confianza como los errores estándar como el “significa\(\pm \) algo”, así que siempre asegúrate de especificar de qué estás hablando.
Todo lo anterior se aplica únicamente a las variables de medición normalmente distribuidas. Para los datos de medición de una distribución altamente no normal, las técnicas de arranque, de las que no voy a hablar aquí, podrían arrojar mejores estimaciones de los límites de confianza.
Límites de confianza para variables nominales
Existe una fórmula diferente, más complicada, basada en la distribución binomial, para calcular límites de confianza de proporciones (datos nominales). Es importante destacar que arroja límites de confianza que no son simétricos alrededor de la proporción, especialmente para proporciones cercanas a cero o uno. John Pezzullo tiene una página web fácil de usar para intervalos de confianza de una proporción. Para ver cómo funciona, digamos que has tomado una muestra de\(20\) hombres y has encontrado\(2\) daltónicos y\(18\) no daltónicos. Vaya a la página web e ingrese\(2\) en el cuadro “Numerador” y\(20\) en el cuadro “Denominador”, luego presione “Computar”. Los resultados para este ejemplo serían un límite de confianza inferior de\(0.0124\) y un límite de confianza superior de\(0.3170\). No se puede reportar la proporción de hombres daltónicos como "\(0.10\pm something\),” en cambio tendrías que decir "\(0.10\)con límites de\(95\%\) confianza de\(0.0124\) y”\(0.3170\).
Una técnica alternativa para estimar los límites de confianza de una proporción supone que las proporciones de la muestra se distribuyen normalmente. Esta técnica aproximada produce límites de confianza simétricos, que para proporciones cercanas a cero o uno son obviamente incorrectos. Por ejemplo, si calculas los límites de confianza usando la aproximación normal\(0.10\) con un tamaño de muestra de\(20\), obtienes\(-0.03\) y\(0.23\), lo cual es ridículo (no podrías tener menos que\(0\%\) de hombres daltónicos). También sería incorrecto decir que los límites de confianza fueron\(0\) y\(0.23\), porque sabes que la proporción de hombres daltónicos en tu población es mayor que\(0\) (tu muestra tenía dos hombres daltónicos, así sabes que la población tiene al menos dos hombres daltónicos). Considero que los límites de confianza para proporciones que se basan en la aproximación normal son obsoletos para la mayoría de los propósitos; se debe usar el intervalo de confianza basado en la distribución binomial, a menos que el tamaño de la muestra sea tan grande que sea computacionalmente poco práctico. Desafortunadamente, más personas usan los límites de confianza basados en la aproximación normal que usan los límites de confianza binomiales correctos.
La fórmula para el intervalo de\(95\%\) confianza usando la aproximación normal es\(p\pm 1.96\sqrt{\left [ \frac{p(1-p)}{n} \right ]}\), donde\(p\) está la proporción y\(n\) es el tamaño de la muestra. Así, para\(P=0.20\) y\(n=100\), el intervalo de confianza sería\(\pm 1.96\sqrt{\left [ \frac{0.20(1-0.20)}{100} \right ]}\), o\(0.20\pm 0.078\). Una regla general común dice que está bien usar esta aproximación siempre y cuando sea mayor que\(5\); mi regla general es usar solo la aproximación normal cuando el tamaño de la muestra es tan grande que calcular el intervalo de confianza binomial exacto haga que salga humo de su computadora.\(npq\)
Pruebas estadísticas con intervalos de confianza
Este manual presenta principalmente estadísticas “clásicas” o “frecuentistas”, en las que se prueban hipótesis estimando la probabilidad de obtener los resultados observados por casualidad, si el nulo es verdadero (el\(P\) valor). Una forma alternativa de hacer estadísticas es poner un intervalo de confianza en una medida de la desviación de la hipótesis nula. Por ejemplo, en lugar de comparar dos medias con una prueba t —de dos muestras, algunos estadísticos calcularían el intervalo de confianza de la diferencia en las medias.
Este enfoque es valioso si una pequeña desviación de la hipótesis nula sería poco interesante, cuando estás más interesado en el tamaño del efecto que en si existe. Por ejemplo, si estás haciendo pruebas finales de un nuevo medicamento en el que confías que tendrá algún efecto, te interesaría principalmente estimar qué tan bien funcionó y qué tan seguro estabas en el tamaño de ese efecto. Querrías que tu resultado fuera “Este medicamento redujo la presión arterial sistólica en\(10.7 mm\; \; Hg\), con un intervalo de confianza de\(7.8\) a”\(13.6\), no “Este medicamento redujo significativamente la presión arterial sistólica (\(P=0.0007\))”.
El uso de los límites de confianza de esta manera, como alternativa a la estadística frecuentista, tiene muchos defensores, y puede ser un enfoque útil. No obstante, a menudo veo gente diciendo cosas como “La diferencia en la presión arterial media fue\(10.7 mm\; \; Hg\), con un intervalo de confianza de\(7.8\) a\(13.6\); porque el intervalo de confianza sobre la diferencia no incluye\(0\), las medias son significativamente diferentes”. Esta es solo una forma torpe y indirecta de hacer pruebas de hipótesis, y solo deberían admitirla y hacer una prueba estadística frecuentista.
Existe el mito de que cuando dos medios tienen intervalos de confianza que se superponen, las medias no son significativamente diferentes (a\(P<0.05\) nivel). Otra versión de este mito es que si cada media está fuera del intervalo de confianza de la otra media, las medias son significativamente diferentes. Ninguno de estos es cierto (Schenker y Gentleman 2001, Payton et al. 2003); es fácil que dos conjuntos de números tengan intervalos de confianza superpuestos, pero aún así sean significativamente diferentes mediante una prueba t de dos muestras; a la inversa, cada media puede estar fuera del intervalo de confianza de la otra, sin embargo, son todavía no significativamente diferentes. No intentes comparar dos medios comparando visualmente sus intervalos de confianza, solo usa la prueba estadística correcta.
Estadísticas similares
Los límites de confianza y el error estándar de la media tienen el mismo propósito, para expresar la confiabilidad de una estimación de la media. Cuando miras artículos científicos, a veces las “barras de error” en las gráficas o el ± número tras medias en las tablas representan el error estándar de la media, mientras que en otros artículos representan intervalos de\(95\%\) confianza. Prefiero intervalos de\(95\%\) confianza. Cuando veo una gráfica con un montón de puntos y barras de error que representan medias e intervalos de confianza, sé que la mayoría (\(95\%\)) de las barras de error incluyen las medias paramétricas. Cuando las barras de error son errores estándar de la media, solo se espera que alrededor de dos tercios de las barras incluyan las medias paramétricas; tengo que duplicar mentalmente las barras para obtener el tamaño aproximado del intervalo de\(95\%\) confianza (porque\(t(0.05)\) es aproximadamente\(2\) para todos menos valores muy pequeños de\(n\)). Cualquiera que sea la estadística que decida usar, asegúrese de dejar claro qué representan las barras de error en sus gráficas. Un sorprendente número de artículos no dicen lo que representan sus barras de error, lo que significa que la única información que las barras de error transmiten al lector es que los autores son descuidados y descuidados.
Ejemplos
Datos de medición
Los datos de dace de nariz negra de la página web de tendencia central tienen una media aritmética de\(70.0\). El límite de confianza inferior es\(45.3\) (\(70.0-24.7\)) y el límite de confianza superior es\(94.7\) (\(70+24.7\)).
Datos nominales
Si trabajas con muchas proporciones, es bueno tener una idea aproximada de los límites de confianza para diferentes tamaños de muestra, así que tienes una idea de cuántos datos necesitarás para una comparación particular. Para proporciones cercanas\(50\%\), los intervalos de confianza son aproximadamente\(\pm 30\%,\; 10\%,\; 3\%\), y\(1\%\) para\(n=10,\; 100,\; 1000,\) y\(10,000\), respectivamente. Es por ello que el “margen de error” en las encuestas políticas, que suelen tener un tamaño muestral de alrededor\(1,000\), suele ser sobre\(3\%\). Por supuesto, esta idea aproximada no sustituye a un análisis de potencia real.
| n | proporción=0.10 | proporción=0.50 |
|---|---|---|
| 10 | 0.0025, 0.4450 | 0.1871, 0.8129 |
| 100 | 0.0490, 0.1762 | 0.3983, 0.6017 |
| 1000 | 0.0821, 0.1203 | 0.4685, 0.5315 |
| 10,000 | 0.0942, 0.1060 | 0.4902, 0.5098 |
Cómo calcular los límites de confianza
Hojas de Cálculo
La hoja de cálculo de estadística descriptiva descriptive.xls calcula los límites de\(95\%\) confianza de la media para hasta\(1000\) mediciones. Los intervalos de confianza para una hoja de cálculo de proporción binomial confidence.xls calcula los límites de\(95\%\) confianza para las variables nominales, utilizando tanto el binomio exacto como la aproximación normal.
Páginas web
Esta página web calcula intervalos de confianza de la media para observaciones de hasta\(10,000\) medición. La página web para intervalos de confianza de una proporción maneja variables nominales.
R
El\(R\) compañero de Salvatore Mangiafico tiene programas R de muestra para límites de confianza tanto para variables de medición como nominales.
SAS
Para obtener límites de confianza para una variable de medición, agregue CIBASIC a la instrucción PROC UNIVARIATE, así:
peces de datos; ubicación de
entrada $ dacenumber;
tarjetas;
Mill_Creek_1 76
Mill_Creek_2 102
North_Branch_Rock_Creek_1 12
North_Branch_Rock_Creek_2 39
Rock_Creek_1 55
Rock_Creek_2 93
Rock_Creek_3 98
Rock_Creek_4 53
Turkey_Branch 102
;
proc univariante data=fish cibasic;
run;
La salida incluirá los límites de\(95\%\) confianza para la media (y para la desviación estándar y varianza, que casi nunca necesitarías):
Límites Básicos de Confianza Suponiendo Normalidad
Parámetro Estimación 95% Límites de Confianza
Media 70.00000 45.33665
94.66335 Desviación estándar 32.08582 21.67259 61.46908
Varianza 1030 469.70135 3778
Esto demuestra que los datos de dace de nariz negra tienen una media de\(70\), con límites de confianza de\(45.3\) y\(94.7\).
Puedes obtener los límites de confianza para una proporción binomial usando PROC FREQ. Aquí está el programa de muestra de la página de prueba exacta de bondad de ajuste:
datos gus;
entrada pata $;
tarjetas;
derecha
izquierda
derecha derecha
derecha
derecha
izquierda
derecha derecha
derecha
derecha
;
proc freq data=gus;
tablas pata/binomio (P = 0.5); binomio
exacto;
corrida;
Y aquí está parte de la salida:
Proporción binomial
para pata = izquierda
—
Proporción 0.2000
ASE 0.1265
95% Límite Conf Inferior 0.0000
95% Límite de Conf Superior 0.4479 Límites Conf
Exactos
95% Límite Conf Inferior 0.0252
95% Límite de Conf Superior 0.5561
El primer par de límites de confianza mostrado se basa en la aproximación normal; el segundo par es el mejor, basado en el cálculo binomial exacto. Tenga en cuenta que si tiene más de dos valores de la variable nominal, los límites de confianza solo se calcularán para el valor cuyo nombre es primero alfabéticamente. Por ejemplo, si el conjunto de datos de Gus incluía “izquierda”, “derecha” y “ambos” como valores, SAS solo calcularía los límites de confianza en la proporción de “ambos”. Una forma torpe de resolver esto sería ejecutar el programa tres veces, cambiar el nombre de “left” a “aleft”, luego cambiar el nombre de “right” a “right”, para hacer cada uno primero en una carrera.
Referencias
- Payton, M. E., M. H. Greenstone, y N. Schenker. 2003. Intervalos de confianza superpuestos o intervalos de error estándar: ¿qué significan en términos de significancia estadística? Revista de Ciencia de Insectos 3:34.
- Schenker, N., y J. F. Gentleman. 2001. Al juzgar la significancia de las diferencias mediante el examen de la superposición entre intervalos de confianza. Estadístico Americano 55:182-186.


