4.5: Homocedasticidad y Heterocedasticidad

Objetivos de aprendizaje

• Las pruebas paramétricas suponen que los datos son homoscedásticos (tienen la misma desviación estándar en diferentes grupos).
• Para aprender a verificar esto y qué hacer si los datos son heteroscedásticos (tienen diferentes desviaciones estándar en diferentes grupos).

Uno de los supuestos de un anova y otras pruebas paramétricas es que las desviaciones estándar dentro del grupo de los grupos son todas iguales (exhiben homocedasticidad). Si las desviaciones estándar son diferentes entre sí (exhiben heterocedasticidad), la probabilidad de obtener un resultado falso positivo aunque la hipótesis nula sea verdadera puede ser mayor que el nivel alfa deseado.

Para ilustrar este problema, hice simulaciones de muestras de tres poblaciones, todas con la misma media poblacional. Simulé tomar muestras de\(10\) observaciones de la población\(A\),\(7\) de la población\(B\) y\(3\) de la población\(C\), y repitió este proceso miles de veces. Cuando las tres poblaciones fueron homoscedásticas (tenían la misma desviación estándar), los anova unidireccionales en los conjuntos de datos simulados fueron significativos (\(P<0.05\)) aproximadamente\(5\%\) del tiempo, como deberían ser. Sin embargo, cuando hice diferentes las desviaciones estándar (\(1.0\)para población\(A\),\(2.0\) para población\(B\) y\(3.0\) para población\(C\)), obtuve un\(P\) valor menor que\(0.05\) en aproximadamente\(18\%\) de las simulaciones. Es decir, a pesar de que los medios poblacionales eran realmente todos iguales, mi posibilidad de obtener un resultado falso positivo era\(18\%\), no la deseada\(5\%\).

Ha habido una serie de estudios de simulación que han tratado de determinar cuándo la heterocedasticidad es un problema lo suficientemente grande como para que se utilicen otras pruebas. La heterocedasticidad es mucho menor cuando se tiene un diseño equilibrado (tamaños de muestra iguales en cada grupo). Los primeros resultados sugirieron que la heterocedasticidad no era un problema en absoluto con un diseño equilibrado (Glass et al. 1972), pero los resultados posteriores encontraron que grandes cantidades de heterocedasticidad pueden inflar la tasa de falsos positivos, incluso cuando los tamaños de muestra son iguales (Harwell et al. 1992). El problema de la heterocedasticidad es mucho peor cuando los tamaños de muestra son desiguales (un diseño desequilibrado) y las muestras más pequeñas son de poblaciones con mayores desviaciones estándar; pero cuando las muestras más pequeñas son de poblaciones con desviaciones estándar más pequeñas, la tasa de falsos positivos en realidad puede ser mucho menos de 0.05, lo que significa que se reduce el poder de la prueba (Glass et al. 1972).

Qué hacer con la heterocedasticidad

Siempre se deben comparar las desviaciones estándar de diferentes grupos de medidas, para ver si son muy diferentes entre sí. Sin embargo, a pesar de todos los estudios de simulación que se han realizado, no parece haber consenso sobre cuándo la heterocedasticidad es un problema lo suficientemente grande como para no usar una prueba que asuma la homocedasticidad.

Si ves una gran diferencia en las desviaciones estándar entre grupos, lo primero que debes probar son las transformaciones de datos. Un patrón común es que los grupos con medias más grandes también tienen desviaciones estándar más grandes, y una transformación log o raíz cuadrada a menudo solucionará este problema. Es mejor si puedes elegir una transformación basada en un estudio piloto, antes de hacer tu experimento principal; no quieres que la gente cínica piense que elegiste una transformación porque te dio un resultado significativo.

Si las desviaciones estándar de sus grupos son muy heterogéneas sin importar qué transformación aplique, hay una gran cantidad de pruebas alternativas para elegir (Lix et al. 1996). La alternativa más utilizada al anova unidireccional es el anova de Welch, a veces llamado t —test de Welch cuando hay dos grupos.

Las pruebas no paramétricas, como la prueba de Kruskal—Wallis en lugar de un anova unidireccional, no asumen normalidad, sino que asumen que las formas de las distribuciones en diferentes grupos son las mismas. Esto significa que las pruebas no paramétricas no son una buena solución al problema de la heterocedasticidad.

Toda la discusión anterior ha sido sobre anovas unidireccionales. La homocedasticidad también es una suposición de otros anóvulos, como los anidados y bidireccionales, y la regresión y correlación. Mucho menos se ha trabajado sobre los efectos de la heterocedasticidad en estas pruebas; todo lo que puedo recomendar es que inspeccione los datos para detectar heterocedasticidad y esperar que no la encuentre, o que una transformación la arregle.

Prueba de Bartlett

Existen varias pruebas estadísticas para la homocedasticidad, y la más popular es la prueba de Bartlett. Utilice esta prueba cuando tenga una variable de medición, una variable nominal, y desee probar la hipótesis nula de que las desviaciones estándar de la variable de medición son las mismas para los diferentes grupos.

La prueba de Bartlett no es particularmente buena, porque es sensible a las desviaciones de la normalidad así como a la heterocedasticidad; no debes entrar en pánico solo porque tienes una prueba significativa de Bartlett. Puede ser más útil usar la prueba de Bartlett para ver qué efecto tienen diferentes transformaciones sobre la heterocedasticidad; puede elegir la transformación con el\(P\) valor más alto (menos significativo) para la prueba de Bartlett.

Una alternativa a la prueba de Bartlett que no voy a cubrir aquí es la prueba de Levene. Es menos sensible a las desviaciones de la normalidad, pero si los datos son aproximadamente normales, es menos potente que la prueba de Bartlett.

Si bien la prueba de Bartlett generalmente se usa al examinar datos para ver si es apropiado para una prueba paramétrica, hay momentos en que probar la igualdad de desviaciones estándar es el objetivo principal de un experimento. Por ejemplo, digamos que quieres saber si la variación en la longitud de zancada entre los corredores está relacionada con su nivel de experiencia, tal vez a medida que la gente corre más, aquellos que comenzaron con zancadas inusualmente largas o cortas convergen gradualmente en alguna longitud de zancada ideal. Se podría medir la longitud de zancada de no corredores, corredores principiantes, corredores aficionados experimentados y corredores profesionales, con varios individuos en cada grupo, luego usar la prueba de Bartlett para ver si hubo una heterogeneidad significativa en las desviaciones estándar.

Cómo hacer la prueba de Bartlett

Hoja de Cálculo

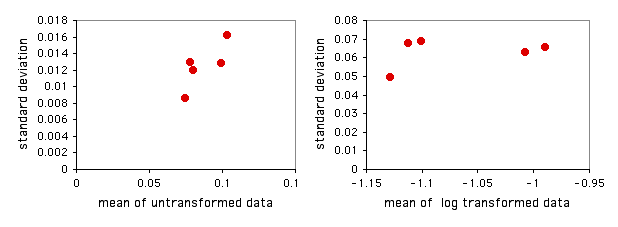
He elaborado una hoja de cálculo que realiza la prueba de Bartlett de homogeneidad de desviaciones estándar bartletts.xls para hasta\(1000\) observaciones en cada uno de hasta\(50\) grupos. Permite ver lo que hará la transformación de log o raíz cuadrada. También se muestra una gráfica de las desviaciones estándar trazadas frente a las medias. Esto le da una rápida visualización de la diferencia en cantidad de variación entre los grupos, y también muestra si la media y la desviación estándar están correlacionadas.

Al ingresar los datos de concha de mejillón de la página web de anova unidireccional en la hoja de cálculo, los\(P\) valores son\(0.655\) para datos no transformados,\(0.856\) para datos transformados de raíz cuadrada y\(0.929\) para datos transformados en logarítmicos. Ninguno de estos es cercano a la significación, así que no hay necesidad real de preocuparse. El gráfico de los datos no transformados indica una correlación entre la media y la desviación estándar, por lo que podría ser una buena idea transformar logarítmica los datos:

Fig. 4.5.1 Desviación estándar frente a AAM promedio para datos no transformados y transformados logarítmicos

Página web

Hay página web para la prueba de Bartlett que manejará hasta\(14\) grupos. Hay que ingresar las varianzas (no desviaciones estándar) y tamaños de muestra, no los datos brutos.

SAS

Puedes usar la opción HOVTEST=BARTLETT en la declaración MEANS de PROC GLM para realizar la prueba de Bartlett. Esta modificación del programa de la página de anova unidireccional hace la prueba de Bartlett.

PROC GLM data=MusselShells;
CLASE location;
MODELO aam = ubicación;
MEANS location/HOVTEST=BARTLETT;
run;

Referencias

Glass, G.V., P.D. Peckham, y J.R. Sanders. 1972. Consecuencias de no cumplir con los supuestos subyacentes a los análisis de efectos fijos de varianza y covarianza. Revisión de Investigación Educativa 42:237-288.

Harwell, M.R., E.N. Rubinstein, W.S. Hayes, y C.C. Olds. 1992. Resumiendo los resultados de Monte Carlo en la investigación metodológica: los casos ANOVA de efectos fijos de uno y dos factores. Revista de Estadística Educativa 17:315-339.

Lix, L.M., J.C. Keselman, y H.J. Keselman. 1996. Consecuencias de violaciones de suposiciones revisadas: Una revisión cuantitativa de alternativas al análisis unidireccional de la prueba F de varianza. Revisión de Investigación Educativa 66:579-619.