5.1: Regresión lineal y correlación

Objetivos de aprendizaje

• Para usar regresión lineal o correlación cuando se quiere saber si una variable de medición está asociada con otra variable de medición; desea medir la fuerza de la asociación (\(r^2\)); o si desea una ecuación que describa la relación y pueda usarse para predecir valores desconocidos.

Una de las gráficas más comunes en la ciencia traza una variable de medición en el eje\(x\) (horizontal) vs. otra en el eje\(y\) (vertical). Por ejemplo, aquí hay dos gráficas. Para el primero, desempolvé la máquina elíptica en nuestro sótano y medí mi pulso después de un minuto de eliptización a varias velocidades:

Velocidad, kph	Pulso, bpm
0	57
1.6	69
3.1	78
4	80
5	85
6	87
6.9	90
7.7	92
8.7	97
12.4	108
15.3	119

Fig. 5.1.1 Gráfica de mi frecuencia de pulso vs. velocidad en una máquina de ejercicios elíptica.

Para la segunda gráfica, desempolvé algunos datos de McDonald (1989): Recogí el crustáceo anfípodo Platorchestia platensis en una playa cerca de Stony Brook, Long Island, en abril de 1987, retiré y conté el número de huevos que llevaba cada hembra, luego se liofilizó y pesó a las madres:

Peso, mg	Huevos
5.38	29
7.36	23
6.13	22
4.75	20
8.10	25
8.62	25
6.30	17
7.44	24
7.26	20
7.17	27
7.78	24
6.23	21
5.42	22
7.87	22
5.25	23
7.37	35
8.01	27
4.92	23
7.03	25
6.45	24
5.06	19
6.72	21
7.00	20
9.39	33
6.49	17
6.34	21
6.16	25
5.74	22

Hay tres cosas que puedes hacer con este tipo de datos. Una es una prueba de hipótesis, para ver si existe una asociación entre las dos variables; en otras palabras, a medida que la\(X\) variable sube, la\(Y\) variable tiende a cambiar (arriba o abajo). Para los datos de ejercicio, querrás saber si la frecuencia del pulso fue significativamente mayor con velocidades más altas. El\(P\) valor es\(1.3\times 10^{-8}\), pero la relación es tan obvia a partir de la gráfica, y tan biológicamente poco sorprendente (¡claro que mi frecuencia del pulso sube cuando hago más ejercicio!) , que la prueba de hipótesis no sería una parte muy interesante del análisis. Para los datos de anfípodos, querría saber si las hembras más grandes tenían más huevos o menos huevos que los anfípodos más pequeños, lo cual no es ni biológicamente obvio ni obvio de la gráfica. Puede parecer una dispersión aleatoria de puntos, pero hay una relación significativa (\(P=0.015)\).

Fig. 5.1.2 Gráfico de número de huevos vs peso seco en el anfípodo Platorchestia platensis.

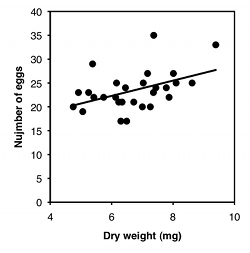
El segundo objetivo es describir qué tan estrechamente están asociadas las dos variables. Esto generalmente se expresa con\(r\), que va de\(-1\) a\(1\), o\(r^2\), que va de\(0\) a\(1\). Para los datos del ejercicio, hay una relación muy estrecha, como lo demuestra el\(r^2\) de\(0.98\); esto significa que si supieras mi velocidad en la máquina elíptica, podrías predecir mi pulso con bastante precisión. El\(r^2\) para los datos de anfípodos es mucho menor, a\(0.21\); esto significa que aunque existe una relación significativa entre el peso de la hembra y el número de huevos, conocer el peso de una hembra no le permitiría predecir con mucha precisión el número de huevos que tenía.

El objetivo final es determinar la ecuación de una línea que atraviesa la nube de puntos. La ecuación de una línea se da en la forma\(\hat{Y}=a+bX\), donde\(\hat{Y}\) está el valor de\(Y\) predicho para un valor dado de\(X\), a es la\(Y\) intercepción (el valor de\(Y\) cuando\(X\) es cero), y\(b\) es la pendiente de la línea (el cambio en\(\hat{Y}\) para un cambio\(X\) de una unidad). Para los datos del ejercicio, la ecuación es\(\hat{Y}=63.5+3.75X\); esto predice que mi pulso sería\(63.5\) cuando la velocidad de la máquina elíptica es\(0 kph\), y mi pulso subiría por\(3.75\) latidos por minuto por cada\(1 kph\) aumento de velocidad. Esta es probablemente la parte más útil del análisis para los datos del ejercicio; si quisiera hacer ejercicio con un nivel particular de esfuerzo, medido por la frecuencia del pulso, podría usar la ecuación para predecir la velocidad que debería usar. Para los datos anfípodos, la ecuación es\(\hat{Y}=12.7+1.60X\). Para la mayoría de los propósitos, solo saber que los anfípodos más grandes tienen significativamente más huevos (la prueba de hipótesis) sería más interesante que conocer la ecuación de la línea, pero depende de los objetivos de tu experimento.

Cuándo utilizarlos

Use correlación/regresión lineal cuando tenga dos variables de medición, como la ingesta de alimentos y peso, la dosis del medicamento y la presión arterial, la temperatura del aire y la tasa metabólica, etc.

También hay una variable nominal que mantiene las dos mediciones juntas en pares, como el nombre de un organismo individual, ensayo experimental o ubicación. No soy consciente de que nadie más considere que esta variable nominal es parte de correlación y regresión, y no es algo de lo que necesites saber el valor, podrías indicar que una medición de la ingesta de alimentos y la medición de peso vinieron de la misma rata poniendo ambos números en la misma línea, sin nunca dándole un nombre a la rata. Por esa razón, la llamaré variable nominal “oculta”.

El valor principal de la variable nominal oculta es que me permite hacer la declaración general de que cada vez que se tienen dos o más medidas de un solo individuo (organismo, ensayo experimental, ubicación, etc.), la identidad de ese individuo es una variable nominal; si solo se tiene una medición de una individual, el individuo no es una variable nominal. Creo que esta regla ayuda a aclarar la diferencia entre anova unidireccional, bidireccional y anidado. Si la idea de variables nominales ocultas en regresión te confunde, puedes ignorarla.

Hay tres objetivos principales para la correlación y regresión en biología. Una es ver si dos variables de medición están asociadas entre sí; ya sea a medida que una variable aumenta, la otra tiende a aumentar (o disminuir). Resumes esta prueba de asociación con el\(P\) valor. En algunos casos, esto aborda una cuestión biológica sobre las relaciones causa-efecto; una asociación significativa significa que diferentes valores de la variable independiente causan diferentes valores de la dependiente. Un ejemplo sería darle a las personas diferentes cantidades de un medicamento y medir su presión arterial. La hipótesis nula sería que no había relación entre la cantidad de fármaco y la presión arterial. Si rechaza la hipótesis nula, concluiría que la cantidad de medicamento provoca los cambios en la presión arterial. En este tipo de experimentos, determinas los valores de la variable independiente; por ejemplo, decides qué dosis del medicamento recibe cada persona. Los datos de ejercicio y pulso son un ejemplo de esto, ya que determiné la velocidad en la máquina elíptica, luego medí el efecto sobre la frecuencia del pulso.

En otros casos, se quiere saber si dos variables están asociadas, sin inferir necesariamente una relación de causa y efecto. En este caso, no se determina ninguna de las variables antes de tiempo; ambas son naturalmente variables y se miden ambas. Si encuentras una asociación, inferyes que la variación en\(X\) puede causar variación en\(Y\), o variación en\(Y\) puede causar variación en\(X\), o variación en algún otro factor puede afectar tanto\(Y\) y\(X\). Un ejemplo sería medir la cantidad de una proteína particular en la superficie de algunas células y el pH del citoplasma de esas células. Si la cantidad de proteína y el pH están correlacionados, puede ser que la cantidad de proteína afecte el pH interno; o el pH interno afecte la cantidad de proteína; o algún otro factor, como la concentración de oxígeno, afecte tanto la concentración de proteína como el pH. A menudo, una correlación significativa sugiere experimentos adicionales para probar una relación de causa y efecto; si la concentración de proteínas y el pH se correlacionaron, es posible que desee manipular la concentración de proteínas y ver qué sucede con el pH, o manipular el pH y medir la proteína, o manipular el oxígeno y ver qué sucede a ambos. Los datos de los anfípodos son otro ejemplo de esto; podría ser que al ser más grandes los anfípodos tengan más huevos, o que tener más huevos haga que las madres sean más grandes (¿tal vez comen más cuando llevan más huevos?) , o algún tercer factor (¿edad? ingesta de alimentos?) hace que los anfípodos sean más grandes y tengan más huevos.

El segundo objetivo de correlación y regresión es estimar la fuerza de la relación entre dos variables; es decir, qué tan cerca están los puntos de la gráfica a la línea de regresión. Resume esto con el\(r^2\) valor. Por ejemplo, digamos que has medido la temperatura del aire (que van desde\(15^{\circ}C\) hasta\(30^{\circ}C\)) y la velocidad de carrera en el lagarto Agama savignyi, y encuentras una relación significativa: los lagartos más cálidos corren más rápido. También querrías saber si existe una relación estrecha (alta\(r^2\)), lo que te diría que la temperatura del aire es el principal factor que afecta a la velocidad de carrera; si la\(r^2\) es baja, te diría que otros factores además de la temperatura del aire también son importantes, y es posible que quieras hacer más experimentos para buscarlos. También es posible que desee saber cómo se compara el\(r^2\) para Agama savignyi con el de otras especies de lagartos, o para Agama savignyi en diferentes condiciones.

El tercer objetivo de correlación y regresión es encontrar la ecuación de una línea que se ajuste a la nube de puntos. Entonces puedes usar esta ecuación para la predicción. Por ejemplo, si has dado a voluntarios dietas con\(500 mg\) a\(2500 mg\) de sal por día, y luego has medido su presión arterial, podrías usar la línea de regresión para estimar cuánto bajaría la presión arterial de una persona si comiera\(500 mg\) menos sal al día.

Correlación versus regresión lineal

Las herramientas estadísticas utilizadas para la prueba de hipótesis, describiendo la cercanía de la asociación y dibujando una línea a través de los puntos, son la correlación y la regresión lineal. Desafortunadamente, encuentro innecesariamente confusas las descripciones de correlación y regresión en la mayoría de los libros de texto. Algunos libros de texto de estadística tienen correlación y regresión lineal en capítulos separados, y hacen que parezca que siempre es importante elegir una técnica u otra. Creo que esto sobreenfatiza las diferencias entre ellos. Otros libros confunden correlación y regresión sin explicar realmente cuál es la diferencia.

Hay diferencias reales entre correlación y regresión lineal, pero afortunadamente, por lo general no importan. La correlación y la regresión lineal dan exactamente el mismo\(P\) valor para la prueba de hipótesis, y para la mayoría de los experimentos biológicos, ese es el único resultado realmente importante. Entonces, si te interesa principalmente el\(P\) valor, no necesitas preocuparte por la diferencia entre correlación y regresión.

En su mayor parte, trataré la correlación y la regresión lineal como diferentes aspectos de un solo análisis, y se puede considerar la correlación/regresión lineal como una única prueba estadística. Ten en cuenta que mi enfoque es probablemente diferente de lo que verás en otros lugares.

La principal diferencia entre correlación y regresión es que en correlación, muestres ambas variables de medición aleatoriamente de una población, mientras que en regresión eliges los valores de la variable independiente (\(X\)). Por ejemplo, digamos que eres un antropólogo forense, interesado en la relación entre la longitud del pie y la altura corporal en humanos. Si encuentras un pie cortado en la escena de un crimen, te gustaría poder estimar la altura de la persona de la que fue cortado. Mides la longitud del pie y la altura corporal de una muestra aleatoria de humanos, obtienes un\(P\) valor significativo y calculas\(r^2\) para ser\(0.72\). Esto es una correlación, porque tomaste medidas de ambas variables en una muestra aleatoria de personas. Por lo tanto,\(r^2\) es una estimación significativa de la fuerza de la asociación entre la longitud del pie y la altura corporal en humanos, y se puede comparar con otros\(r^2\) valores. Es posible que desee ver si el\(r^2\) para pies y la altura es mayor o menor que el\(r^2\) para las manos y la altura, por ejemplo.

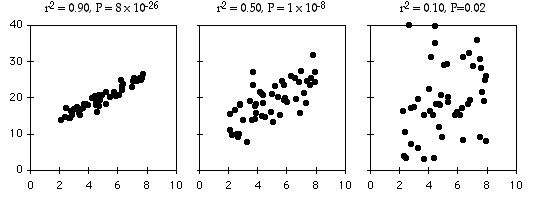
Como ejemplo de regresión, digamos que has decidido que la antropología forense es demasiado repugnante, así que ahora te interesa el efecto de la temperatura del aire en la velocidad de carrera en lagartos. Pones algunos lagartos en una cámara de temperatura configurada para\(10^{\circ}C\), los persigue y graba lo rápido que corren. Haces lo mismo para\(10\) diferentes temperaturas, que van hasta\(30^{\circ}C\). Esto es una regresión, porque decidiste qué temperaturas usar. Probablemente todavía querrás calcular\(r^2\), solo porque los valores altos son más impresionantes. Pero no es una estimación muy significativa de nada sobre lagartos. Esto se debe a que el\(r^2\) depende de los valores de la variable independiente que elija. Para exactamente la misma relación entre temperatura y velocidad de funcionamiento, un rango de temperaturas más estrecho daría una menor\(r^2\). Aquí hay tres gráficas que muestran algunos datos simulados, con la misma dispersión (desviación estándar) de\(Y\) valores en cada valor de\(X\). Como puede ver, con un rango de\(X\) valores más estrecho, el\(r^2\) se hace más pequeño. Si hiciste otro experimento sobre humedad y velocidad de carrera en tus lagartijas y obtuviste un menor\(r^2\), no podrías decir que la velocidad de carrera está más fuertemente asociada con la temperatura que con la humedad; si hubieras elegido un rango de temperaturas más estrecho y un rango más amplio de humedades, la humedad podría tener tenía una temperatura\(r^2\) mayor que.

Fig. 5.1.2 Datos simulados que muestran el efecto del rango de\(X\) valores sobre el\(r^2\). Para los mismos datos exactos, medir\(Y\) en un rango más pequeño de\(X\) valores produce un menor\(r^2\).

Si intentas clasificar cada experimento como regresión o correlación, rápidamente descubrirás que hay muchos experimentos que no entran claramente en una categoría. Por ejemplo, digamos que estudias la temperatura del aire y la velocidad de funcionamiento en lagartos. Usted sale al desierto todos los sábados durante los ocho meses del año en que sus lagartos están activos, mide la temperatura del aire, luego persigue lagartos y mide su velocidad. No has elegido deliberadamente la temperatura del aire, solo tomaste una muestra de la variación natural en la temperatura del aire, entonces ¿es una correlación? Pero no tomaste una muestra de todo el año, solo esos ocho meses, y no escogiste días al azar, solo los sábados, entonces ¿es una regresión?

Si te interesa principalmente utilizar el\(P\) valor para las pruebas de hipótesis, para ver si existe una relación entre las dos variables, no importa si llamas a la prueba estadística regresión o correlación. Si estás interesado en comparar la fuerza de la relación (\(r^2\)) con la fuerza de otras relaciones, estás haciendo una correlación y debes diseñar tu experimento para que midas\(X\) y\(Y\) sobre una muestra aleatoria de individuos. Si determinas los\(X\) valores antes de hacer el experimento, estás haciendo una regresión y no debes interpretar el\(r^2\) como una estimación de algo general sobre la población que has observado.

Correlación y causalidad

Probablemente hayas escuchado a la gente advertirte, “La correlación no implica causalidad”. Esto es un recordatorio de que cuando se está muestreando la variación natural en dos variables, también hay variación natural en muchas posibles variables de confusión que podrían causar la asociación entre\(A\) y\(B\). Entonces, si ves una asociación significativa entre\(A\) y\(B\), no necesariamente significa que la variación en\(A\) causa variación en\(B\); puede haber alguna otra variable\(C\),, que afecte a ambos. Por ejemplo, digamos que fuiste a una escuela primaria, encontraste alumnos\(100\) al azar, midiste cuánto tiempo les tomó atarse los zapatos y midió la longitud de sus pulgares. Estoy bastante seguro de que encontrarías una fuerte asociación entre las dos variables, con pulgares más largos asociados con tiempos más cortos de atadura de zapatos. Estoy seguro de que podrías llegar a una explicación biomecánica inteligente y sofisticada de por qué tener pulgares más largos hace que los niños se aten los zapatos más rápido, completo con vectores de fuerza y ángulos de momento y ecuaciones y\(3-D\) modelado. Sin embargo, eso sería una tontería; tu muestra de estudiantes\(100\) aleatorios tiene variación natural en otra variable, la edad, y los estudiantes mayores tienen pulgares más grandes y tardan menos tiempo en atarse los zapatos.

Entonces, ¿y si te aseguras de que todos tus estudiantes voluntarios tengan la misma edad y aún veas una asociación significativa entre el tiempo de atadura de zapatos y la longitud del pulgar? ¿Esa correlación implicaría causalidad? No, porque piensa en por qué diferentes niños tienen pulgares de diferente longitud. Algunas personas son genéticamente más grandes que otras; ¿podrían los genes que afectan el tamaño general también afectar las habilidades motoras finas? Tal vez. La nutrición afecta el tamaño, y la economía familiar afecta la nutrición; ¿podrían los niños pobres tener pulgares más pequeños debido a la mala nutrición, y también tener tiempos más lentos de atar zapatos porque sus padres tenían demasiado trabajo para enseñarles a atarse los zapatos, o porque eran tan pobres que no obtuvieron sus primeros zapatos hasta ¿llegaron a la edad escolar? Tal vez. No sé, tal vez algunos niños pasan tanto tiempo chupándose el pulgar que el pulgar en realidad se alarga, y tener un pulgar viscoso cubierto de saliva hace que sea más difícil agarrar un cordón. Pero habría múltiples explicaciones plausibles para la asociación entre la longitud del pulgar y el tiempo de atadura del zapato, y sería incorrecto concluir “Los pulgares más largos te hacen atar los zapatos más rápido”.

Ya que es posible pensar en múltiples explicaciones para una asociación entre dos variables, ¿eso significa que debes burlarte cínicamente? “¡La correlación no implica causalidad!” y descartar cualquier estudio de correlación de variación natural? No. Por un lado, observar una correlación entre dos variables sugiere que está sucediendo algo interesante, algo que quizás quieras investigar más a fondo. Por ejemplo, estudios han demostrado una correlación entre comer más frutas y verduras frescas y bajar la presión arterial. Es posible que la correlación sea porque las personas con más dinero, que pueden pagar frutas y verduras frescas, tienen vidas menos estresantes que las personas pobres, y es la diferencia en el estrés lo que afecta la presión arterial; también es posible que las personas que están preocupadas por su salud coman más frutas y verduras y ejercicio más, y es el ejercicio el que afecta la presión arterial. Pero la correlación sugiere que comer frutas y verduras puede reducir la presión arterial. Querría probar esta hipótesis más a fondo, buscando la correlación en muestras de personas con estatus socioeconómico y niveles de ejercicio similares; controlando estadísticamente posibles variables de confusión usando técnicas como regresión múltiple; haciendo estudios en animales; o dando humanos voluntarios controlaron dietas con diferentes cantidades de frutas y verduras. Si tu estudio de correlación inicial no hubiera encontrado una asociación de la presión arterial con frutas y verduras, no tendrías razón para hacer estos estudios adicionales. La correlación puede no implicar causalidad, pero te dice que algo interesante está pasando.

En un estudio de regresión, se establecen los valores de la variable independiente y se controlan o aleatorizan todas las posibles variables de confusión. Por ejemplo, si estás investigando la relación entre la presión arterial y el consumo de frutas y verduras, podrías pensar que es el potasio en las frutas y verduras lo que baja la presión arterial. Podrías investigar esto consiguiendo un grupo de voluntarios del mismo sexo, edad y nivel socioeconómico. Usted elige al azar la ingesta de potasio para cada persona, le das las pastillas adecuadas, haz que tomen las pastillas durante un mes y luego mida su presión arterial. Todas las posibles variables de confusión son controladas (edad, sexo, ingresos) o aleatorias (ocupación, estrés psicológico, ejercicio, dieta), por lo que si ves una asociación entre la ingesta de potasio y la presión arterial, la única causa posible sería que el potasio afecte la presión arterial. Entonces, si has diseñado tu experimento correctamente, la regresión sí implica causalidad.

Hipótesis nula

La hipótesis nula de correlación/regresión lineal es que la pendiente de la línea de mejor ajuste es igual a cero; en otras palabras, a medida que la\(X\) variable se agranda, la\(Y\) variable asociada no llega a ser mayor ni menor.

También es posible probar la hipótesis nula de que el\(Y\) valor predicho por la ecuación de regresión para un valor dado de\(X\) es igual a alguna expectativa teórica; lo más común sería probar la hipótesis nula de que es la\(Y\) intercepción\(0\). Esto rara vez es necesario en experimentos biológicos, así que no lo voy a cubrir aquí, pero ten en cuenta que es posible.

Variables independientes vs. dependientes

Cuando se está probando una relación de causa y efecto, la variable que causa la relación se llama variable independiente y la traza en el\(X\) eje, mientras que el efecto se llama la variable dependiente y la traza en el\(Y\) eje. En algunos experimentos estableces la variable independiente a valores que hayas elegido; por ejemplo, si te interesa el efecto de la temperatura sobre la tasa de llamada de ranas, podrías poner ranas en cámaras de temperatura ajustadas a\(10^{\circ}C\)\(15^{\circ}C\),\(20^{\circ}C\),, etc. En otros casos, ambas variables exhiben variación natural, pero cualquier relación de causa y efecto sería de una manera; si mide la temperatura del aire y la tasa de llamadas de ranas en un estanque en varias noches diferentes, tanto la temperatura del aire como la tarifa de llamadas mostrarían una variación natural, pero si hay una relación de causa y efecto, es temperatura que afecta la velocidad de llamada; la velocidad a la que llaman las ranas no afecta la temperatura del aire.

A veces no está claro cuál es la variable independiente y cuál es la dependiente, aunque pienses que puede haber una relación de causa y efecto. Por ejemplo, si estás probando si el contenido de sal en los alimentos afecta la presión arterial, podrías medir el contenido de sal de las dietas de las personas y su presión arterial, y tratar el contenido de sal como la variable independiente. Pero si estuvieras probando la idea de que la presión arterial alta hace que las personas anhelen alimentos ricos en sal, harías que la presión arterial sea la variable independiente y la ingesta de sal sea la variable dependiente.

A veces, no estás buscando en absoluto una relación de causa y efecto, solo quieres ver si dos variables están relacionadas. Por ejemplo, si mides el rango de movimiento de la cadera y el hombro, no estás tratando de ver si las caderas más flexibles causan hombros más flexibles, o los hombros más flexibles causan caderas más flexibles; en cambio, solo estás tratando de ver si las personas con caderas más flexibles también tienden a tener hombros más flexibles, presumiblemente debido a algún factor (edad, dieta, ejercicio, genética) que afecta la flexibilidad general. En este caso, sería completamente arbitraria qué variable pones en el\(X\) eje y cuál pones en el\(Y\) eje.

Afortunadamente, el\(P\) valor y el no\(r^2\) se ven afectados por qué variable llamas a la\(X\) y a la que llamas a la\(Y\); obtendrás valores matemáticamente idénticos de cualquier manera. La línea de regresión de mínimos cuadrados sí depende de qué variable es la\(X\) y cuál es la\(Y\); las dos líneas pueden ser bastante diferentes si la\(r^2\) es baja. Si realmente te interesa solo si las dos variables covarían, y no estás tratando de inferir una relación de causa y efecto, es posible que quieras evitar usar la línea de regresión lineal como decoración en tu gráfica.

Los investigadores en algunos campos tradicionalmente ponen la variable independiente en el\(Y\) eje. Los oceanógrafos, por ejemplo, suelen trazar profundidad en el\(Y\) eje (con\(0\) en la parte superior) y una variable que se ve directa o indirectamente afectada por la profundidad, como la concentración de clorofila, en el\(X\) eje. No lo recomendaría a menos que sea una tradición muy fuerte en tu campo, ya que podría generar confusión sobre qué variable estás considerando la variable independiente en una regresión lineal.

Cómo funciona la prueba

Fig. 5.1.3 La gráfica muestra los puntos de datos (puntos), la línea de regresión lineal (línea gruesa) y los puntos de datos conectados al punto de la línea de regresión con el mismo valor X (líneas finas). La línea de regresión es la línea que minimiza la suma de las distancias verticales cuadradas entre los puntos y la línea.

Línea de Regresión

La regresión lineal encuentra la línea que mejor se ajusta a los puntos de datos. En realidad, hay varias definiciones diferentes de “mejor ajuste” y, por lo tanto, una serie de métodos diferentes de regresión lineal que se ajustan a líneas algo diferentes. Con mucho, la más común es la “regresión ordinaria de mínimos cuadrados”; cuando alguien solo dice “regresión por mínimos cuadrados” o “regresión lineal” o “regresión”, significan regresión ordinaria de mínimos cuadrados.

En la regresión ordinaria de mínimos cuadrados, el “mejor” ajuste se define como la línea que minimiza las distancias verticales cuadradas entre los puntos de datos y la línea. Para un punto de datos con un\(X\) valor de\(X_1\) y un\(Y\) valor de\(Y_1\), se calcula la diferencia entre\(Y_1\) y\(\hat{Y_1}\) (el valor predicho de\(Y\) at\(X_1\)), luego al cuadrado. Esta desviación al cuadrado se calcula para cada punto de datos, y la suma de estos desviados cuadrados mide qué tan bien se ajusta una línea a los datos. La línea de regresión es aquella para la que esta suma de desviación al cuadrado es menor. Dejaré de lado las matemáticas que se utilizan para encontrar la pendiente e intercepción de la línea de mejor ajuste; eres biólogo y tienes cosas más importantes en las que pensar.

La ecuación para la línea de regresión generalmente se expresa como\(\hat{Y}=a+bX\), donde\(a\) está la\(Y\) intersección y\(b\) es la pendiente. Una vez que sepas\(a\) y\(b\), puedes usar esta ecuación para predecir el valor de\(Y\) para un valor dado de\(X\). Por ejemplo, la ecuación para el experimento de velocidad-frecuencia cardíaca es\(\text{rate}=63.357+3.749\times \text{speed}\). Podría usar esto para predecir que para una velocidad de\(10 kph\), mi frecuencia cardíaca sería\(100.8 bpm\). Debe hacer este tipo de predicción dentro del rango de\(X\) valores que se encuentran en el conjunto de datos original (interpolación). Predecir\(Y\) valores fuera del rango de valores observados (extrapolación) a veces es interesante, pero puede producir fácilmente resultados ridículos si vas lejos del rango observado de\(X\). En el ejemplo de rana a continuación, podría predecir matemáticamente que el intervalo entre llamadas sería de aproximadamente\(16\) segundos en\(-40^{\circ}C\). En realidad, el intervalo entre llamadas sería infinito a esa temperatura, porque todas las ranas estarían congeladas sólidas.

A veces se quiere predecir\(X\) de\(Y\). El uso más común de esto es construir una curva estándar. Por ejemplo, podrías pesar algo de proteína seca y disolverla en agua para hacer soluciones que contengan\(0,\; 100,\; 200…1000\; µg\) proteína por\(ml\), agregar algunos reactivos que dan vuelta de color en presencia de proteína, luego medir la absorbancia de luz de cada solución usando un espectrofotómetro. Entonces, cuando se tiene una solución con una concentración desconocida de proteína, se agregan los reactivos, se mide la absorbancia de luz y se estima la concentración de proteína en la solución.

Existen dos métodos comunes a\(X\) partir de los cuales se puede estimar\(Y\). Una forma es hacer la regresión habitual con\(X\) como variable independiente y\(Y\) como variable dependiente; para el ejemplo proteico, tendrías proteína como variable independiente y absorbancia como variable dependiente. Obtienes la ecuación habitual,\(\hat{Y}=a+bX\), luego la reordenas para resolverla\(X\), dándote\(\hat{X}=\frac{(Y-a)}{b}\). Esto se llama “estimación clásica”.

El otro método es hacer regresión lineal con\(Y\) como la variable independiente y\(X\) como la variable dependiente, también conocida como regresión\(X\) sobre\(Y\). Para la curva estándar de proteínas, harías una regresión con la absorbancia como\(X\) variable y la concentración de proteína como\(Y\) variable. A continuación, usa esta ecuación de regresión para predecir valores desconocidos de\(X\) from\(Y\). Esto se conoce como “estimación inversa”.

Varios estudios de simulación han sugerido que la estimación inversa da una estimación más precisa\(X\) que la estimación clásica (Krutchkoff 1967, Krutchkoff 1969, Lwin y Maritz 1982, Kannan et al. 2007), así que eso es lo que recomiendo. Sin embargo, algunos estadísticos prefieren la estimación clásica (Sokal y Rohlf 1995, pp. 491-493). Si el\(r^2\) es alto (los puntos están cerca de la línea de regresión), la diferencia entre estimación clásica y estimación inversa es bastante pequeña. Cuando estás construyendo una curva estándar para algo así como la concentración de proteínas, la\(r^2\) suele ser tan alta que la diferencia entre la estimación clásica e inversa será trivial. Pero los dos métodos pueden dar estimaciones bastante diferentes de\(X\) cuándo los puntos originales se dispersaron alrededor de la línea de regresión. Para los datos de ejercicio y pulso, con una\(r^2\) de\(0.98\), estimación clásica predice que para obtener un pulso de\(100 bpm\), debo correr a\(9.8 kph\), mientras que la estimación inversa predice una velocidad de\(9.7 kph\). Los datos de anfípodos tienen una cantidad mucho menor\(r^2\) de\(0.25\), por lo que la diferencia entre las dos técnicas es mayor; si quiero saber qué tamaño anfípodo tendría\(30\) huevos, estimación clásica predice un tamaño de\(10.8 mg\), mientras que la estimación inversa predice un tamaño de\(7.5 mg\).

A veces tu objetivo al trazar una línea de regresión no es predecir\(Y\) desde\(X\), o predecir\(X\) desde\(Y\), sino describir la relación entre dos variables. Si una variable es la variable independiente y la otra es la variable dependiente, debe usar la línea de regresión de mínimos cuadrados. Sin embargo, si no existe una relación causa-efecto entre las dos variables, la línea de regresión de mínimos cuadrados es inapropiada. Esto se debe a que obtendrá dos líneas diferentes, dependiendo de qué variable elija para ser la variable independiente. Por ejemplo, si quieres describir la relación entre la longitud del pulgar y la longitud del dedo gordo del pie, obtendrías una línea si hicieras que la longitud del pulgar fuera la variable independiente, y una línea diferente si hicieras que la longitud del dedo gordo fuera la variable independiente. La elección sería completamente arbitraria, ya que no hay razón para pensar que la longitud del pulgar causa variación en la longitud del dedo gordo, o viceversa.

Se han propuesto varias líneas diferentes para describir la relación entre dos variables con una relación simétrica (donde ninguna es la variable independiente). El método más común es la regresión reducida del eje mayor (también conocida como regresión estándar del eje mayor o regresión de la media geométrica). Da una línea que es intermedia en pendiente entre la línea de regresión de mínimos cuadrados de\(Y\) on\(X\) y la línea de regresión de mínimos cuadrados de\(X\) on\(Y\); de hecho, la pendiente de la línea del eje mayor reducido es la media geométrica de las dos líneas de regresión de mínimos cuadrados.

Si bien la regresión reducida del eje mayor da una línea que de alguna manera es una mejor descripción de la relación simétrica entre dos variables (McArdle 2003, Smith 2009), se deben tener en cuenta dos cosas. Una es que no debes usar la línea reducida del eje mayor para predecir valores de\(X\) from\(Y\), o\(Y\) from\(X\); aún debes usar la regresión de mínimos cuadrados para la predicción. La otra cosa que hay que saber es que no se puede probar la hipótesis nula de que la pendiente de la línea del eje mayor reducido es cero, porque es matemáticamente imposible tener una pendiente reducida del eje mayor que sea exactamente cero. Incluso si tu gráfica muestra una línea reducida del eje mayor, tu\(P\) valor es la prueba del nulo de que la línea de regresión de mínimos cuadrados tiene una pendiente de cero.

Coeficiente de determinación (\(r^2\))

Fig. 5.1.4 Tres relaciones con la misma pendiente, misma intercepción y diferentes cantidades de dispersión alrededor de la línea de mejor ajuste.

El coeficiente de determinación, o\(r^2\), expresa la fuerza de la relación entre las\(Y\) variables\(X\) y. Es la proporción de la variación en la\(Y\) variable lo que se “explica” por la variación en la\(X\) variable. \(r^2\)puede variar de\(0\) a\(1\); valores cercanos a la\(1\) media los\(Y\) valores caen casi a la derecha en la línea de regresión, mientras que los valores cercanos a la\(0\) media hay muy poca relación entre\(X\) y\(Y\). Como puedes ver, las regresiones pueden tener una pequeña\(r^2\) y no parecer que haya alguna relación, sin embargo, todavía podrían tener una pendiente que es significativamente diferente de cero.

Para ilustrar el significado de r ², aquí hay seis pares de valores X e Y:

X	Y	Desviarse de la media	Desviación cuadrada
1	2	8	64
3	9	1	1
5	9	1	1
6	11	1	1
7	14	4	16
9	15	5	25
	suma de cuadrados:		108

Si no sabías nada del\(X\) valor y te dijeron que adivinaras qué era un\(Y\) valor, tu mejor conjetura sería la media\(Y\); para este ejemplo, la media\(Y\) es\(10\). El cuadrado desviado de los\(Y\) valores de su media es la suma total de cuadrados, familiar a partir del análisis de varianza. Las líneas verticales de la gráfica izquierda a continuación muestran las desviaciones de la media; el primer punto tiene una desviación de\(8\), por lo que su desviación cuadrada es\(64\), etc. La suma total de cuadrados para estos números es\(64+1+1+1+16+25=108\).

Fig. 5.1.5 Desviaciones de la media Y y de la línea de regresión.

Si supieras el\(X\) valor y te dijeran que adivinaras lo que era un\(Y\) valor, calcularías la ecuación de regresión y la usarías. La ecuación de regresión para estos números es\(\hat{Y}=2.0286+1.5429X\), así que para el primer\(X\) valor se predeciría un\(Y\) valor de\(2.0286+1.5429\times 1=3.5715\), etc. Las líneas verticales en la gráfica derecha de arriba muestran las desviaciones de los\(Y\) valores reales de los\(\hat{Y}\) valores predichos. Como puede ver, la mayoría de los puntos están más cerca de la línea de regresión que a la media general. Al cuadrar estos desvíos y tomar la suma nos da la regresión suma de cuadrados, que para estos números es\(10.8\).

X	Y	Valor Y previsto	Desviarse de lo predicho	Desviación cuadrada
1	2	3.57	1.57	2.46
3	9	6.66	2.34	5.48
5	9	9.74	0.74	0.55
6	11	11.29	0.29	0.08
7	14	12.83	1.17	1.37
9	15	15.91	0.91	0.83
		Suma de regresión de cuadrados:		10.8

La suma de regresión de cuadrados es\(10.8\), que es\(90\%\) menor que la suma total de cuadrados (\(108\)). Esta diferencia entre las dos sumas de cuadrados, expresada como una fracción de la suma total de cuadrados, es la definición de\(r^2\). En este caso diríamos eso\(r^2=0.90\); la\(X\) variable “explica”\(90\%\) de la variación en la\(Y\) variable.

El\(r^2\) valor se conoce formalmente como el “coeficiente de determinación”, aunque suele llamarse simplemente\(r^2\). La raíz cuadrada de\(r^2\), con signo negativo si la pendiente es negativa, es el coeficiente de correlación producto-momento de Pearson\(r\), o simplemente “coeficiente de correlación”. Se puede utilizar cualquiera\(r\) o\(r^2\) para describir la fuerza de la asociación entre dos variables. Yo prefiero\(r^2\), porque se usa con más frecuencia en mi área de biología, tiene un significado más comprensible (la diferencia proporcional entre la suma total de cuadrados y la suma de regresión de cuadrados), y no tiene esos molestos valores negativos. Debes familiarizarte con la literatura en tu campo y usar la medida que sea más común. Una situación en la que r es más útil es si se ha realizado regresión lineal/correlación para múltiples conjuntos de muestras, con algunas pendientes positivas y otras con pendientes negativas, y desea saber si el coeficiente de correlación medio es significativamente diferente de cero; ver McDonald y Dunn (2013) por una aplicación de esta idea.

Estadística de prueba

El estadístico de prueba para una regresión lineal es\(t_s=\frac{\sqrt{d.f.}\times r^2}{\sqrt{(1-r^2)}}\). Se hace más grande a medida que los grados de libertad (\(n-2\)) se hacen más grandes o los\(r^2\) se hacen más grandes. Bajo la hipótesis nula, el estadístico de\(t\) prueba se distribuye con\(n-2\) grados de libertad. Al reportar los resultados de una regresión lineal, la mayoría de las personas solo dan la r ² y los grados de libertad, no el\(t_s\) valor. Cualquiera que realmente necesite el\(t_s\) valor puede calcularlo a partir de los grados\(r^2\) y de libertad.

Para el ritmo cardiaco—datos de velocidad, el\(r^2\) es\(0.976\) y hay\(9\) grados de libertad, por lo que la\(t_s\) estadística es\(19.2\). Es significativo (\(P=1.3\times 10^{-8}\)).

Algunas personas cuadran\(t_s\) y obtienen una\(F\) -estadística con\(1\) grado de libertad en el numerador y\(n-2\) grados de libertad en el denominador. El\(P\) valor resultante es matemáticamente idéntico al calculado con\(t_s\).

Debido a que el valor P es una función tanto del tamaño de la muestra como del tamaño de la muestra, no debe usar el\(P\) valor como una medida de la fuerza de asociación.\(r^2\) Si la correlación de\(A\) y\(B\) tiene un\(P\) valor menor que la correlación de\(A\) y\(C\), no necesariamente significa eso\(A\) y\(B\) tienen una asociación más fuerte; podría ser simplemente que el conjunto de datos para el\(A\)\(B\) experimento fue más grandes. Si quieres comparar la fuerza de asociación de diferentes conjuntos de datos, debes usar\(r\) o\(r^2\).

Supuestos

Normalidad y homocedasticidad

Dos supuestos, similares a los del anova, son que para cualquier valor de\(X\), los\(Y\) valores se distribuirán normalmente y serán homoscedásticos. Aunque rara vez tendrás datos suficientes para probar estos supuestos, a menudo son violados.

Afortunadamente, numerosos estudios de simulación han demostrado que la regresión y la correlación son bastante robustas a las desviaciones de la normalidad; esto significa que aunque una o ambas de las variables no sean normales, el\(P\) valor será menor que\(0.05\) aproximadamente\(5\%\) del tiempo si la hipótesis nula es verdadera ( Edgell y Noon 1984, y referencias en ellos). Entonces, en general, se puede utilizar la regresión/correlación lineal sin preocuparse por la no normalidad.

A veces verás una regresión o correlación que parece que puede ser significativa debido a que uno o dos puntos son extremos tanto en el\(x\)\(y\) eje como. En este caso, es posible que desee utilizar la correlación de rangos de Spearman, que reduce la influencia de valores extremos, o puede que desee encontrar una transformación de datos que haga que los datos se vean más normales. Otro enfoque sería analizar los datos sin los valores extremos, y reportar los resultados con o sin ellos puntos periféricos; tu vida será más fácil si los resultados son similares con o sin ellos.

Cuando hay una regresión o correlación significativa,\(X\) los valores con\(Y\) valores medios más altos a menudo también tendrán desviaciones estándar más altas de\(Y\). Esto sucede porque la desviación estándar suele ser una proporción constante de la media. Por ejemplo, las personas que miden\(1.5\) metros de altura podrían tener un peso medio de\(50 kg\) y una desviación estándar de\(10 kg\), mientras que las personas que miden\(2\) metros de altura podrían tener un peso medio de\(100 kg\) y una desviación estándar de\(20 kg\). Cuando la desviación estándar de\(Y\) es proporcional a la media, se puede hacer que los datos sean homoscedásticos con una transformación logarítmica de la\(Y\) variable.

Linealidad

La regresión lineal y la correlación suponen que los datos se ajustan a una línea recta. Si miras los datos y la relación se ve curvada, puedes probar diferentes transformaciones de datos del\(X\), el, o ambos\(Y\), y ver cuál hace que la relación sea recta. Por supuesto, es mejor si eliges una transformación de datos antes de analizar tus datos. Puede elegir una transformación de datos de antemano en función de los datos anteriores que haya recopilado, o en función de la transformación de datos que otros en su campo usen para su tipo de datos.

Una transformación de datos a menudo enderezará una curva en forma de J. Si tu curva se ve en forma de U, en forma de S o algo más complicado, una transformación de datos no la convertirá en una línea recta. En ese caso, tendrás que usar regresión curvilínea.

Independencia

La regresión lineal y la correlación suponen que los puntos de datos son independientes entre sí, lo que significa que el valor de un punto de datos no depende del valor de ningún otro punto de datos. La violación más común de este supuesto en regresión y correlación es en los datos de series de tiempo, donde alguna\(Y\) variable se ha medido en diferentes momentos. Por ejemplo, los biólogos han contado el número de alces en Isle Royale, una isla grande en el Lago Superior, cada año. Los alces viven mucho tiempo, por lo que el número de alces en un año no es independiente del número de alces del año anterior, es altamente dependiente de él; si el número de alces en un año es alto, el número en el próximo año probablemente será bastante alto, y si el número de alces es bajo un año, el número lo hará probablemente también sea baja el próximo año. Este tipo de no independencia, o “autocorrelación”, puede darle una regresión o correlación “significativa” mucho más a menudo que\(5\%\) de la época, incluso cuando la hipótesis nula de no relación entre el tiempo y\(Y\) es cierta. Si ambos\(X\) y\(Y\) son series de tiempo —por ejemplo, analizas el número de lobos y el número de alces en Isle Royale— también puedes conseguir una relación “significativa” entre ellos con demasiada frecuencia.

Para ilustrar lo fácil que es engañarse con datos de series temporales, probé la correlación entre el número de alces en Isle Royale en el invierno y el número de ponches lanzados por los equipos de béisbol de Grandes Ligas la siguiente temporada, utilizando datos para 2004-2013. Lo hice por separado para cada equipo de beisbol, así que hubo 30 pruebas estadísticas. Estoy bastante seguro de que la hipótesis nula es cierta (no se me ocurre nada que afecte tanto a la abundancia de alces en el invierno como a los ponches del verano siguiente), así que con los equipos de\(30\) béisbol, se esperaría que el\(P\) valor sea menor que\(0.05\) para los equipos, o alrededor\(5\%\) de uno o dos. En cambio, el\(P\) valor es significativo para\(7\) los equipos, lo que significa que si fueras lo suficientemente estúpido como para probar la correlación de números de alces y ponches por parte de tu equipo favorito, tendrías casi una\(4\) oportunidad\(1\) -in- de convencerte de que había una relación entre los dos. Algunas de las correlaciones se ven bastante bien: los números de ponche del equipo de Cleveland y los números de alces tienen un\(r^2\) de\(0.70\) y un\(P\) valor de\(0.002\):

Fig. 5.1.6 Número de alces en Isle Royale y ponches del equipo de béisbol de Cleveland, mostrando lo fácil que es obtener una correlación de aspecto impresionante a partir de dos conjuntos de datos autocorrelacionados.

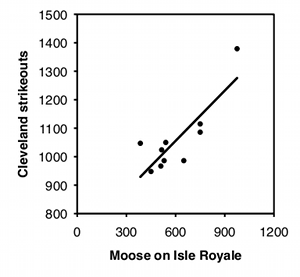
Existen pruebas estadísticas especiales para datos de series temporales. No los voy a cubrir aquí; si necesitas usarlos, mira cómo otras personas en tu campo han analizado datos similares a los tuyos, entonces infórmate más sobre los métodos que utilizaron.

La autocorrelación espacial es otra fuente de no independencia. Esto ocurre cuando se mide una variable en ubicaciones que están lo suficientemente cercanas entre sí como para que las ubicaciones cercanas tenderán a tener valores similares. Por ejemplo, si quieres saber si la abundancia de dientes de león está asociada con la cantidad de fosfato en el suelo, podrías marcar un manojo de\(1 m^2\) cuadrados en un campo, contar el número de dientes de león en cada cuadrata y medir la concentración de fosfato en el suelo de cada cuadrata. Sin embargo, es probable que tanto la abundancia de diente de león como la concentración de fosfato se autocorrelacionen espacialmente; si un cuadrante tiene muchos dientes de león, sus cuadrantes vecinos también tendrán muchos dientes de león, por razones que pueden no tener nada que ver con el fosfato. De manera similar, la composición del suelo cambia gradualmente en la mayoría de las áreas, por lo que un cuadrante con bajo contenido de fosfato probablemente estará cerca de otros cuadrantes que son bajos en fosfato. Sería fácil encontrar una correlación significativa entre la abundancia de diente de león y la concentración de fosfato, aunque no exista una relación real. Si necesitas aprender sobre la autocorrelación espacial en ecología, Dale y Fortín (2009) es un buen lugar para comenzar.

Otra área donde la autocorrelación espacial es un problema es el análisis de imágenes. Por ejemplo, si etiquetas una proteína verde y otra proteína roja, entonces observa la cantidad de proteína roja y verde en diferentes partes de una célula, el alto nivel de autocorrelación entre los píxeles vecinos hace que sea muy fácil encontrar una correlación entre la cantidad de proteína roja y verde, incluso si no hay verdadera relación. Ver McDonald y Dunn (2013) para una solución a este problema.

Ejemplo

Una observación común en ecología es que la diversidad de especies disminuye a medida que se aleja del ecuador. Para ver si este patrón se podía ver a pequeña escala, utilicé datos del Conteo de Aves Navideñas de la Sociedad Audubon, en el que los observadores de aves intentan contar todas las aves en un área de\(15\; mile\) diámetro durante un día de invierno. Observé el número total de especies observadas en cada área de la Península de Delmarva durante el conteo de 2005. La latitud y el número de especies de aves son las dos variables de medición; la ubicación es la variable nominal oculta.

Ubicación	Latitud	Número de especies
Bombay Hook, DE	39.217	128
Cape Henlopen, DE	38.8	137
Middletown	39.467	108
Milford	38.958	118
Rehoboth	38.6	135
Seaford-Nanticoke	38.583	94
Wilmington	39.733	113
Crisfield	38.033	118
Denton (Maryland)	38.9	96
Elkton	39.533	98
Condado de Lower Kent	39.133	121
Ocean City (MD)	38.317	152
Salisbury	38.333	108
Condado de S. Dorchester	38.367	118
Cape Charles (Virginia)	37.2	157
Chincoteague	37.967	125
Wachapreague	37.667	114

Fig. 5.1.7 Latitud y especies de aves en la Península de Delmarva.

El resultado es\(r^2=0.214\), con\(15 d.f.\), entonces el\(P\) valor es\(0.061\). La tendencia está en la dirección esperada, pero no es del todo significativa. La ecuación de la línea de regresión es\(\text {number of species}=-12.039\times \text {latitude}+585.14\). Aunque fuera significativo, no sé qué harías con la ecuación; supongo que podrías extrapolarla y usarla para predecir que por encima del\(49^{th}\) paralelo, habría menos de cero especies de aves.

Fig. 5.1.8 Rana arbórea gris, Hyla versicolor.

Fig. 5.1.9 Relación de temperatura corporal e intervalo entre llamadas en la rana arbórea gris.

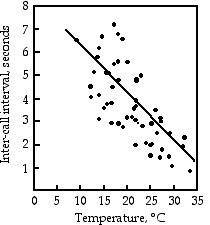
Gayou (1984) midió los intervalos entre las llamadas de apareamiento macho en la rana arbórea gris, Hyla versicolor, a diferentes temperaturas. La línea de regresión es\(\text {interval}=-0.205\times \text{temperature}+8.36\), y es altamente significativa (\(r^2=0.29,\; 45 d.f.,\; P=9\times 10^{-5}\)). Se podría reorganizar la ecuación,\(\text{temperature}=\frac{(\text{interval}-8.36)}{(-0.205)}\), medir el intervalo entre las llamadas de apareamiento de ranas, y estimar la temperatura del aire. O podrías comprar un termómetro.

Goheen et al. (2003) capturaron ratones\(14\) hembra saltamontes norteños (Onchomys leucogaster) en el centro-norte de Kansas, midieron la longitud corporal y contaron el número de crías. Existen dos variables de medición, longitud corporal y número de crías, y a los autores les interesó saber si un mayor tamaño corporal provoca un aumento en el número de crías, por lo que hicieron una regresión lineal. Los resultados son significativos:\(r^2=0.46,\; 12 d.f.,\; P=0.008\). La ecuación de la línea de regresión es\(\text{offspring}=0.108\times \text{length}-7.88\).

Graficando los resultados

En una hoja de cálculo, se muestran los resultados de una regresión en un gráfico de dispersión, con la variable independiente en el\(X\) eje. Para agregar la línea de regresión a la gráfica, termine de hacer la gráfica, luego seleccione la gráfica y vaya al menú Gráfico. Elija “Agregar línea de tendencia” y elija la línea recta. Si desea mostrar la línea de regresión que se extiende más allá del rango observado de\(X\) valores, elija “Opciones” y ajuste los números de “Previsión” hasta obtener la línea que desea.

Pruebas similares

A veces no está claro si un experimento incluye una variable de medición y dos variables nominales, y debe analizarse con un anova bidireccional o una prueba t pareada, o incluye dos variables de medición y una variable nominal oculta, y debe analizarse con correlación y regresión. En ese caso, tu elección de prueba está determinada por la pregunta biológica que te interesa. Por ejemplo, digamos que has medido el rango de movimiento del hombro derecho y hombro izquierdo de un grupo de personas diestras. Si tu pregunta es “¿Existe una asociación entre el rango de movimiento de los hombros derecho e izquierdo de las personas, las personas con hombros derechos más flexibles también tienden a tener hombros izquierdos más flexibles?” , trataría “rango de movimiento del hombro derecho” y “rango de movimiento del hombro izquierdo” como dos variables de medición diferentes, e individual como una variable nominal oculta, y analizaría con correlación y regresión. Si tu pregunta es “¿El hombro derecho es más flexible que el hombro izquierdo?” , tratarías “rango de movimiento” como una variable de medición, “derecha vs izquierda” como una variable nominal, individual como una variable nominal, y analizarías con anova bidireccional o una\(t\) prueba —pareada.

Si la variable dependiente es un porcentaje, como el porcentaje de personas que tienen ataques cardíacos en diferentes dosis de un medicamento, en realidad es una variable nominal, no una medida. Cada observación individual es un valor de la variable nominal (“ataque al corazón” o “sin ataque cardíaco”); el porcentaje no es realmente una sola observación, es una forma de resumir un montón de observaciones. Un enfoque para los datos porcentuales es transformar los porcentajes de arcseno y analizar con correlación y regresión lineal. Verás esto en la literatura, y no es horrible, pero es mejor analizarlo usando regresión logística.

Si la relación entre las dos variables de medición se describe mejor mediante una línea curva, no una recta, una posibilidad es probar diferentes transformaciones en una o ambas variables. La otra opción es usar regresión curvilínea.

Si una o ambas de tus variables son variables clasificadas, no de medición, debes usar la correlación de rangos de Spearman. Algunas personas recomiendan la correlación de rangos de Spearman cuando no se cumplen los supuestos de regresión lineal/correlación (normalidad y homocedasticidad), pero no estoy al tanto de ninguna investigación que demuestre que Spearman es realmente mejor en esta situación.

Para comparar las pendientes o intercepciones de dos o más líneas de regresión entre sí, use ancova.

Si tiene más de dos variables de medición, utilice regresión múltiple.

Cómo hacer la prueba

Hoja de Cálculo

He elaborado una hoja de cálculo regression.xls para hacer regresión lineal y correlación sobre hasta\(1000 pairs\) de observaciones. Proporciona lo siguiente:

• El coeficiente de regresión (la pendiente de la línea de regresión).
• El\(Y\) intercepto. Con la pendiente y la intercepción, se tiene la ecuación para la línea de regresión:\(\hat{Y}=a+bX\), donde\(a\) está la\(y\) intercepción y\(b\) es la pendiente.
• El\(r^2\) valor.
• Los grados de libertad. Hay\(n-2\) grados de libertad en una regresión, donde\(n\) está el número de observaciones.
• El\(P\) valor. Esto le da la probabilidad de encontrar una pendiente que sea tan grande o mayor que la pendiente observada, bajo la hipótesis nula de que la pendiente verdadera es\(0\).
• Un\(Y\) estimador y un\(X\) estimador. Esto le permite ingresar un valor de\(X\) y encontrar el valor correspondiente de\(Y\) en la línea de mejor ajuste, o viceversa. Esto sería útil para construir curvas estándar, tales como las utilizadas en ensayos de proteínas, por ejemplo.

Páginas web

Las páginas web que realizarán regresión lineal están aquí, aquí y aquí. Todos requieren que ingrese cada número individualmente, y por lo tanto son inconvenientes para grandes conjuntos de datos. Esta página web hace regresión lineal y le permite pegar en un conjunto de números, lo cual es más conveniente para grandes conjuntos de datos.

R

El\(R\) compañero de Salvatore Mangiafico tiene un programa R de muestra para correlación y regresión lineal.

SAS

Puedes usar PROC GLM o PROC REG para una regresión lineal simple; dado que PROC REG también se usa para regresión múltiple, también podrías aprender a usarlo. En la sentencia MODEL, le das primero la\(Y\) variable, luego la\(X\) variable después del signo igual. Aquí hay un ejemplo usando los datos de aves de arriba.

DATA aves;
INPUT pueblo $ estado $ latitud especies;
DATALINES;

Bombay_Hook DE 39.217 128
Cape_Henlopen DE 38.800 137
Middletown DE 39.467 108
Milford DE 38.958 118
Rehoboth DE 38.600 135
Seaford-Nanticoke DE 38.583 94
Wilmington DE 39.733 113
Crisfield MD 38.033 118
Denton MD 38.900 96
Elkton MD 39.533 98
Bajo_Kent_County MD 39.133 121
Ocean_City MD 38.317 152
Salisbury MD 38.333 108
S_Dorchester_County MD 38.367 118
Cape_Charles VA 37.200 157
Chincoteague VA 37.967 125
Wachapreague VA 37.667 114
;
PROC REG data=Aves;
MODELO especies=latitud;
RUN;
La salida incluye una tabla de análisis de varianza. No se alarme por esto; si profundiza en las matemáticas, la regresión es solo otra variedad de anova. Debajo de la tabla anova se encuentran la pendiente\(r^2\), la intersección y\(P\) el valor:

Raíz MSE 16.37357 R-Square 0.2143 r ² Media
dependiente 120.00000 Adj R-Sq 0.1619
Coeff Var 13.64464

Parámetro Estimaciones Parámetro
Variable Estándar DF Estimación Error t Valor Pr > |t|


intercepción Intercepción 1 585.14462 230.02416 2.54 0.0225
latitud 1 -12.03922 5.95277 -2.02 0.0613
Pendiente del valor P
Estos resultados indican un\(r^2\) de\(0.21\), intercepción de\(585.1\), una pendiente de\(-12.04\), y un\(P\) valor de\(0.061\).

Análisis de potencia

El programa G*Power calculará el tamaño de muestra necesario para una regresión/correlación. El tamaño del efecto es el valor absoluto del coeficiente de correlación\(r\); si se tiene\(r^2\), tome la raíz cuadrada positiva del mismo. Elija “t tests” en el menú “Familia de pruebas” y “Correlación: Modelo biserial puntual” del menú “Prueba estadística”. Ingresa el\(r\) valor que esperas ver, tu alfa (usualmente\(0.05\)) y tu potencia (usualmente\(0.80\) o\(0.90\)).

Por ejemplo, digamos que quieres buscar una relación entre la tarifa de llamadas y la temperatura en la rana arbórea ladrona, Hyla gratiosa. Gayou (1984) encontró un\(r^2\) de\(0.29\) en otra especie de ranas, H. versicolor, así que decides que quieres poder detectar una\(r^2\) de\(0.25\) o más. La raíz cuadrada de\(0.25\) es\(0.5\), por lo que se ingresa\(0.5\) para “Tamaño del efecto”,\(0.05\) para alfa, y\(0.8\) para poder. El resultado son\(26\) observaciones de temperatura y tasa de llamada de rana.

Es importante señalar que la distribución de\(X\) las variables, en este caso las temperaturas del aire, debe ser la misma para el estudio propuesto que para el estudio piloto en el que se basó el cálculo del tamaño de la muestra. Gayou (1984) midió la tasa de llamada de ranas a temperaturas que se distribuyeron de manera bastante uniforme de\(10^{\circ}C\) a\(34^{\circ}C\). Si observas un rango de temperaturas más estrecho, necesitarías muchas más observaciones para detectar el mismo tipo de relación.

Referencias

Dale, M.R.T., y M.-J. Fortín. 2009. Autocorrelación espacial y pruebas estadísticas: algunas soluciones. Revista de Estadísticas Agrícolas, Biológicas y Ambientales 14:188-206.

Edgell, S.E., y S.M. Mediodía. 1984. Efecto de la violación de la normalidad sobre la prueba t del coeficiente de correlación. Boletín Psicológico 95:576-583.

Gayou, D.C. 1984. Efectos de la temperatura en la llamada de apareamiento de Hyla versicolor. Copeia 1984:733-738.

Goheen, J.R., G.A. Kaufman, y D.W. Kaufman. 2003. Efecto del tamaño corporal sobre las características reproductivas del ratón saltamontes norteño en el centro-norte de Kansas. Naturalista del sudoeste 48:427-431.

Kannan, N., J.P. Keating, y R.L. Mason. 2007. Comparación de estimadores clásicos e inversos en el problema de calibración. Comunicaciones en Estadística: Teoría y Métodos 36:83-95.

Krutchkoff, R.G. 1967. Métodos clásicos y de regresión inversa de calibración. Tecnometría 9:425-439.

Krutchkoff, R.G. 1969. Métodos de regresión clásica e inversa de calibración en extrapolación. Tecnometría 11:605-608.

Lwin, T., y J.S. Maritz. 1982. Un análisis de la controversia de calibración lineal desde la perspectiva de la estimación compuesta. Tecnometría 24:235-242.

McCardle, B.H. 2003. Líneas, modelos y errores: Regresión en campo. Limnología y Oceanografía 48:1363-1366.

McDonald, J.H. 1989. Análisis de componentes de selección del locus Mpl en el anfípodo Platorchestia platensis. Herencia 62:243-249.

McDonald, J.H., y K.W. Dunn. 2013. Pruebas estadísticas para medidas de colocalización en microscopía biológica. Diario de Microscopía 252:295-302.

Smith, R.J. 2009. Uso y mal uso del eje mayor reducido para el ajuste de línea. Revista Americana de Antropología Física 140:476-486.

Sokal, R.R., y F.J. Rohlf. 1995. Biometría. W.H. Freeman, Nueva York.