12.2: Efectos Parciales

Última actualización
Guardar como PDF

Page ID: 150253

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como se señala en el Capítulo 1, la regresión múltiple controla” para los efectos de otras variables sobre las variables dependientes. Esto es con el fin de gestionar posibles relaciones espurias, donde la variable ZZ influye en el valor tanto de XX como de YY. La figura\(\PageIndex{1}\) ilustra la naturaleza de las relaciones espurias entre variables.

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'

Figura\(\PageIndex{1}\): Relaciones espurias

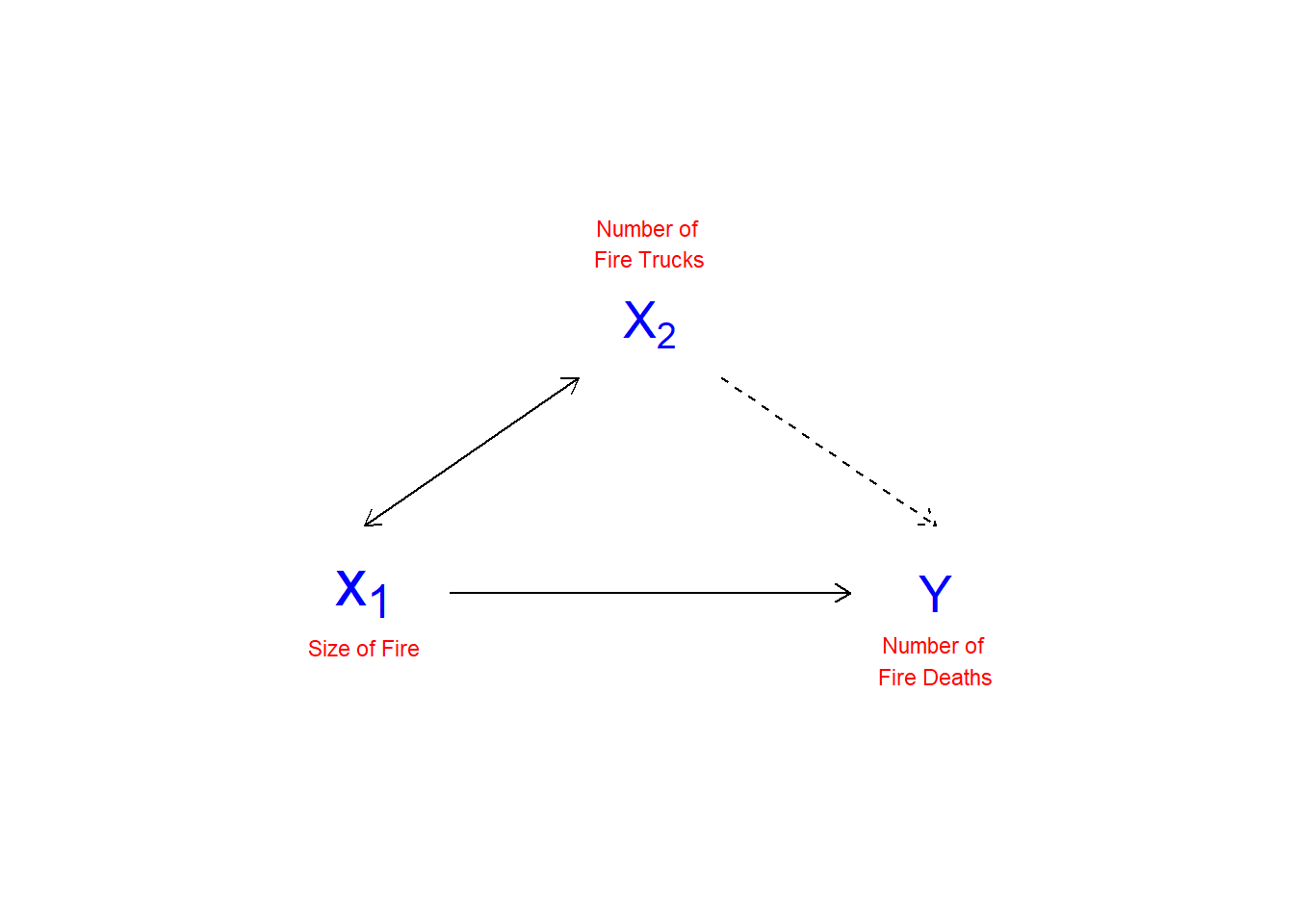
Para controlar las relaciones espurias, la regresión múltiple da cuenta de los efectos parciales de un XX sobre otro XX. Los efectos parciales se refieren a la varianza compartida entre YY y XX, lo que se ilustra en la Figura\(\PageIndex{2}\). En este ejemplo, el número de muertes resultantes de incendios domiciliarios se asocia positivamente con el número de camiones de bomberos que se envían al lugar del incendio. Un análisis simple concluiría que si se envían menos camiones, se producirían menos muertes relacionadas con incendios. Por supuesto, el número de camiones enviados al incendio, y el número de muertes relacionadas con el fuego, son ambos impulsados por la magnitud del incendio. Un control adecuado del tamaño del incendio, por lo tanto presumiblemente eliminaría la asociación positiva entre el número de camiones de bomberos en el lugar y el número de muertes (e incluso podría revertir la dirección de la relación, ya que el mayor número de camiones puede suprimir más rápidamente el incendio).

## Warning: Removed 1 rows containing missing values (geom_point).

## Warning: Removed 1 rows containing missing values (geom_point).

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'

## Warning in is.na(x): is.na() applied to non-(list or vector) of type
## 'expression'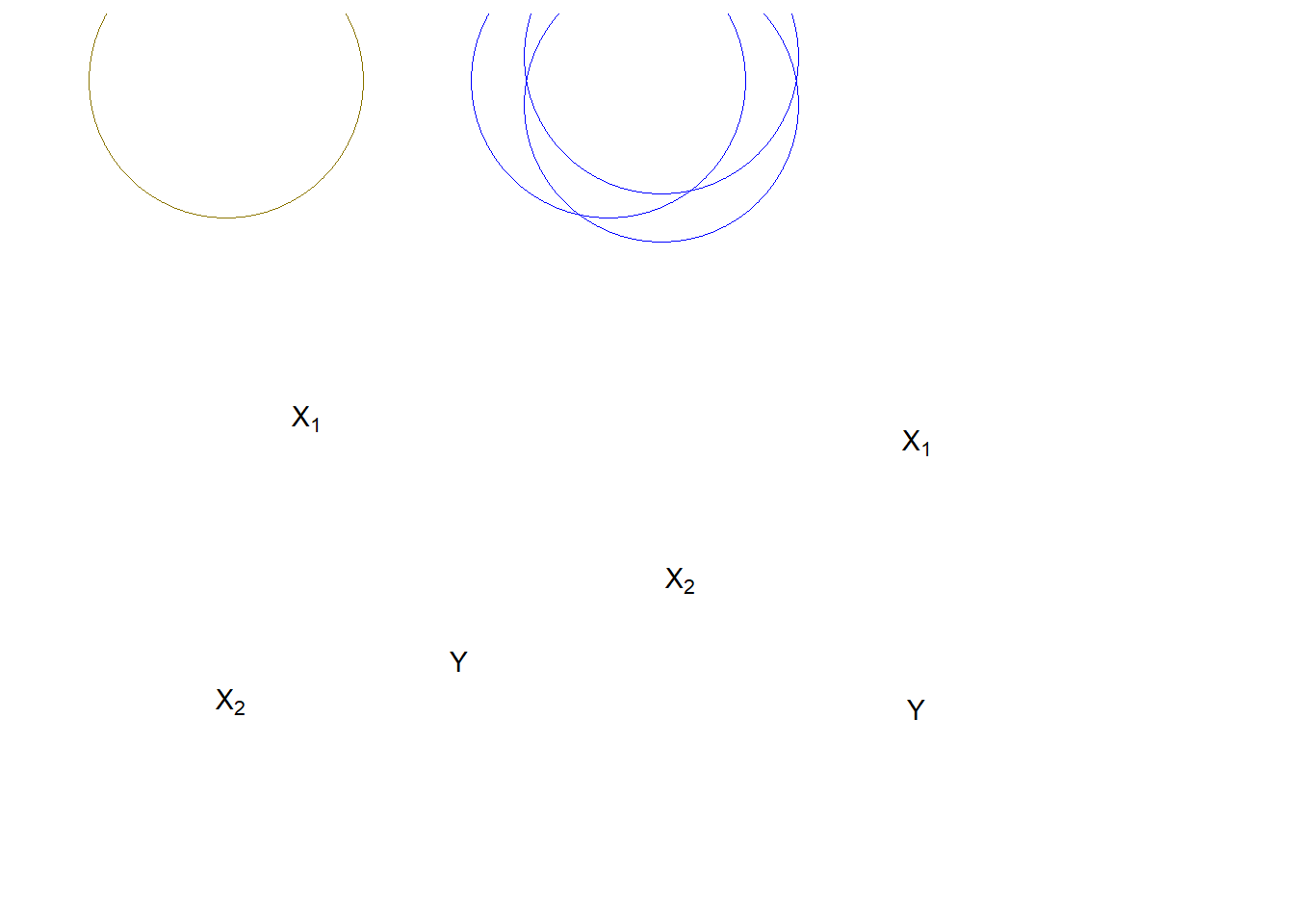

Figura\(\PageIndex{2}\): Efectos Parciales

En la Figura\(\PageIndex{2}\), el diagrama de Venn de la izquierda muestra un par de XXs que conjuntamente predecirían YY mejor que cualquiera de los XX solos. Sin embargo, el área solapada entre X1X1 y X2X2 causa cierta confusión. Eso habría que eliminar para estimar el efecto “puro” de X1X1 en YY. El diagrama de la derecha representa un caso peligroso. En general, X1X1+X2X2 explican bien YY, pero no sabemos cómo influye el individuo X1X1 o X2X2 en YY. Esto nubla nuestra capacidad de ver los efectos de cualquiera de los XSxS en YY. En el caso extremo de explicaciones totalmente superpuestas por los IVs, nos enfrentamos a la condición de multicolinealidad que hace imposible la estimación de los coeficientes de regresión parcial (los BSB).

Al calcular el efecto de X1X1 en YY, necesitamos eliminar el efecto de los otros XXs tanto en X1X1 como en YY. Si bien la regresión múltiple hace esto por nosotros, caminaremos por un ejemplo para ilustrar los conceptos.

Efectos Parciales

En un caso con dos IVs, X1X1 y X2X2

y=a+b1xi1+b2xi2+eiy=a+b1xi1+b2xi2+ei

Eliminar el efecto de X2X2 y YY

^YI=A1+B1Xi2+EIY|x2YI^=A1+B1Xi2+EIY|x2

Eliminar el efecto de X2X2 en X1X1:

^Xi=A2+B2XI2+EIX1|X2XI^=A2+B2XI2+EIX1|X2

Entonces,

EIY|x2=0+B3eIX1|x2EIY|x2=0+B3eIX1|x2 y B3eIX1|x2=B1XI1B3eIX1|x2=B1xi1

Como ejemplo, utilizaremos la edad y la ideología para predecir el riesgo percibido del cambio climático.

ds.temp <- filter(ds) %>% dplyr::select(glbcc_risk, ideol, age) %>%
  na.omit()

ols1 <- lm(glbcc_risk ~ ideol+age, data = ds.temp)
summary(ols1)

## 
## Call:
## lm(formula = glbcc_risk ~ ideol + age, data = ds.temp)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.7913 -1.6252  0.2785  1.4674  6.6075 
## 
## Coefficients:
##              Estimate Std. Error t value            Pr(>|t|)    
## (Intercept) 11.096064   0.244640  45.357 <0.0000000000000002 ***
## ideol       -1.042748   0.028674 -36.366 <0.0000000000000002 ***
## age         -0.004872   0.003500  -1.392               0.164    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.479 on 2510 degrees of freedom
## Multiple R-squared:  0.3488, Adjusted R-squared:  0.3483 
## F-statistic: 672.2 on 2 and 2510 DF,  p-value: < 0.00000000000000022

Obsérvese que el coeficiente estimado para ideología es -1.0427478. Para ver cómo la regresión múltiple elimina la varianza compartida primero retrocedemos el riesgo de cambio climático en la edad y creamos un objeto ols2.resids de los residuales.

ols2 <- lm(glbcc_risk ~ age, data = ds.temp)
summary(ols2)

## 
## Call:
## lm(formula = glbcc_risk ~ age, data = ds.temp)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.4924 -2.1000  0.0799  2.5376  4.5867 
## 
## Coefficients:
##              Estimate Std. Error t value             Pr(>|t|)    
## (Intercept)  6.933835   0.267116  25.958 < 0.0000000000000002 ***
## age         -0.016350   0.004307  -3.796              0.00015 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.062 on 2511 degrees of freedom
## Multiple R-squared:  0.005706,   Adjusted R-squared:  0.00531 
## F-statistic: 14.41 on 1 and 2511 DF,  p-value: 0.0001504

ols2.resids <- ols2$residuals

Nótese que, al modelarse solo, el efecto estimado de la edad en glbccrsk es mayor (-0.0164) que en la regresión múltiple con ideología (-0.00487). Esto se debe a que la edad se correlaciona con la ideología, y —porque la ideología también está relacionada con glbccrsk— cuando no “controlamos” la ideología, la variable de edad conlleva parte de la influencia de la ideología.

A continuación, retrocedemos la ideología sobre la edad y creamos un objeto de los residuos.

ols3 <- lm(ideol ~ age, data = ds.temp)
summary(ols3)

## 
## Call:
## lm(formula = ideol ~ age, data = ds.temp)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.9492 -0.8502  0.2709  1.3480  2.7332 
## 
## Coefficients:
##             Estimate Std. Error t value             Pr(>|t|)    
## (Intercept) 3.991597   0.150478  26.526 < 0.0000000000000002 ***
## age         0.011007   0.002426   4.537           0.00000598 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.725 on 2511 degrees of freedom
## Multiple R-squared:  0.00813,    Adjusted R-squared:  0.007735 
## F-statistic: 20.58 on 1 and 2511 DF,  p-value: 0.000005981

ols3.resids <- ols3$residuals

Finalmente, retrocedemos los residuos de ols2 en los residuales de ols3. Tenga en cuenta que esta regresión no incluye un término de intercepción.

ols4 <- lm(ols2.resids ~ 0 + ols3.resids)
summary(ols4)

## 
## Call:
## lm(formula = ols2.resids ~ 0 + ols3.resids)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.7913 -1.6252  0.2785  1.4674  6.6075 
## 
## Coefficients:
##             Estimate Std. Error t value            Pr(>|t|)    
## ols3.resids -1.04275    0.02866  -36.38 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.478 on 2512 degrees of freedom
## Multiple R-squared:  0.3451, Adjusted R-squared:  0.3448 
## F-statistic:  1324 on 1 and 2512 DF,  p-value: < 0.00000000000000022

Como se muestra, el BB estimado para EIX1|X2EIX1|X2, coincide con el BB estimado para ideología en la primera regresión. Lo que hemos hecho, y lo que hace la regresión múltiple, está limpio” tanto YY como X1X1 (ideología) de sus correlaciones con X2X2 (edad) mediante el uso de los residuales de las regresiones bivariadas.