3.2: Medidas de Tendencia Central
- Page ID
- 150690
En el apartado anterior vimos que hay varias formas de definir tendencia central. Esta sección define las tres medidas más comunes de tendencia central: la media, la mediana y el modo. Las relaciones entre estas medidas de tendencia central y las definiciones dadas en el apartado anterior probablemente no te serán obvias.
En esta sección se dan únicamente las definiciones básicas de la media, mediana y modo. En una sección posterior se presenta una discusión adicional sobre los méritos relativos y las aplicaciones adecuadas de estas estadísticas.
Media Aritmética
La media aritmética es la medida más común de tendencia central. Es simplemente la suma de los números divididos por el número de números. El símbolo “\(\mu \)” (pronunciado “mew”) se utiliza para la media de una población. El símbolo “\(\overline{\mathrm{X}}\)” (pronunciado “X-bar”) se utiliza para la media de una muestra. La fórmula para\(\mu \) se muestra a continuación:
\[\mu=\dfrac{\sum \mathrm{X}}{N}\]
donde\(\Sigma \mathbf{X} \) está la suma de todos los números en la población y\(N\) es el número de números en la población.
La fórmula para\(\overline{\mathrm{X}} \) es esencialmente idéntica:
\[\overline{\mathrm{X}}=\dfrac{\sum \mathrm{X}}{N} \]
donde\(\Sigma \mathbf{X} \) es la suma de todos los números en la muestra y\(N\) es el número de números en la muestra. La única distinción entre estas dos ecuaciones es si nos estamos refiriendo a la población (en cuyo caso usamos el parámetro\(\mu \)) o una muestra de esa población (en cuyo caso usamos el estadístico\(\overline{\mathrm{X}}\)).
A modo de ejemplo, la media de los números 1, 2, 3, 6, 8 es 20/5 = 4 independientemente de que los números constituyan toda la población o sólo una muestra de la población.
La figura\(\PageIndex{1}\) muestra el número de pases de touchdown (TD) lanzados por cada uno de los 31 equipos de la Liga Nacional de Futbol en la temporada 2000. El número medio de pases de touchdown lanzados es 20.45 como se muestra a continuación.
\[\mu=\dfrac{\sum X}{N}=\dfrac{634}{31}=20.45 \nonumber \]
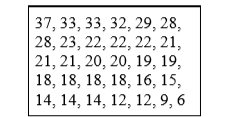
Si bien la media aritmética no es la única “media” (también hay una media geométrica, una media armónica, y muchas otras que están todas fuera del alcance de este curso), es con mucho la más utilizada. Por lo tanto, si se usa el término “media” sin especificar si es la media aritmética, la media geométrica, o alguna otra media, se supone que se refiere a la media aritmética.
Mediana La mediana también es una medida de tendencia central de uso frecuente. La mediana es el punto medio de una distribución: el mismo número de puntuaciones está por encima de la mediana que por debajo de ella. Para los datos de la Figura\(\PageIndex{1}\), hay 31 puntajes. La puntuación 16 más alta (que equivale a 20) es la mediana porque hay 15 puntuaciones por debajo de la puntuación 16 y 15 puntuaciones por encima de la puntuación 16. La mediana también se puede considerar como el percentil 50.
Cuando hay un número impar de números, la mediana es simplemente el número medio. Por ejemplo, la mediana de 2, 4 y 7 es 4. Cuando hay un número par de números, la mediana es la media de los dos números medios. Así, la mediana de los números 2, 4, 7, 12 es:
\[\dfrac{4+7}{2}=5.5 \nonumber \]
Cuando hay números con los mismos valores, cada aparición de ese valor se cuenta. Por ejemplo, en el conjunto de números 1, 3, 4, 4, 5, 8 y 9, la mediana es 4 porque hay tres números (1, 3 y 4) por debajo y tres números (5, 8 y 9) por encima de él. Si solo contáramos 4 una vez, la mediana se calcularía incorrectamente en 4.5 (4+5 dividido por 2). En caso de duda, escribir todos los números en orden y marcarlos uno a la vez desde arriba e abajo siempre te llevará a la respuesta correcta.
Modo
El modo es el valor que ocurre con mayor frecuencia en el conjunto de datos. Para los datos de la Figura\(\PageIndex{1}\), el modo es 18 ya que más equipos (4) tuvieron 18 pases de touchdown que cualquier otro número de pases de touchdown. Con datos continuos, como el tiempo de respuesta medido a muchos decimales, la frecuencia de cada valor es uno ya que no hay dos puntuaciones exactamente iguales (ver discusión de variables continuas). Por lo tanto, el modo de datos continuos normalmente se calcula a partir de una distribución de frecuencia agrupada. \(\PageIndex{1}\)La tabla muestra una distribución de frecuencia agrupada para los datos de tiempo de respuesta objetivo. Dado que el intervalo con la frecuencia más alta es 600-700, el modo es el medio de ese intervalo (650). Aunque el modo no se utiliza frecuentemente para datos continuos, es sin embargo una medida importante de tendencia central, ya que es la única medida que podemos usar en datos cualitativos o categóricos.
| Rango | Frecuencia |
|---|---|
| 500 - 600 | 3 |
| 600 - 700 | 6 |
| 700 - 800 | 5 |
| 800 - 900 | 5 |
| 900 - 1000 | 0 |
| 1000 - 1100 | 1 |
Más sobre la media y la mediana
En la sección “Qué es tendencia central”, vimos que el centro de una distribución podría definirse de tres maneras:
- el punto en el que se equilibraría una distribución
- el valor cuya desviación absoluta promedio de todos los demás valores se minimiza
- el valor cuya diferencia al cuadrado de todos los demás valores se minimiza.
La media es el punto en el que se equilibraría una distribución, la mediana es el valor que minimiza la suma de las desviaciones absolutas, y la media es el valor que minimiza la suma de las desviaciones cuadradas.
En el cuadro se\(\PageIndex{2}\) muestran las desviaciones absolutas y cuadradas de los números 2, 3, 4, 9 y 16 a partir de su mediana de 4 y su media de 6.8. Se puede ver que la suma de las desviaciones absolutas de la mediana (20) es menor que la suma de las desviaciones absolutas de la media (22.8). Por otro lado, la suma de las desviaciones cuadradas de la mediana (174) es mayor que la suma de las desviaciones cuadradas de la media (134.8).
| Valor | Desviación absoluta de la mediana | Desviación absoluta de la media | Desviación cuadrada de la mediana | Desviación cuadrada de la media |
|---|---|---|---|---|
| 2 | 2 | 4.8 | 4 | 23.04 |
| 3 | 1 | 3.8 | 1 | 14.44 |
| 4 | 0 | 2.8 | 0 | 7.84 |
| 9 | 5 | 2.2 | 25 | 4.84 |
| 16 | 12 | 9.2 | 144 | 84.64 |
| Total | 20 | 22.8 | 174 | 134.8 |
La figura\(\PageIndex{2}\) muestra que la distribución se equilibra a la media de 6.8 y no a la mediana de 4. Las ventajas y desventajas relativas de la media y la mediana se discuten en la sección “Comparando medidas” más adelante en este capítulo.

Cuando una distribución es simétrica, entonces la media y la mediana son las mismas. Considera la siguiente distribución: 1, 3, 4, 5, 6, 7, 9. La media y la mediana son ambas 5. La media, mediana y modo son idénticos en la distribución normal acampanada.
Comparando Medidas de Tendencia Central
¿Cómo se comparan entre sí las diversas medidas de tendencia central? Para distribuciones simétricas, la media y mediana, como es el modo excepto en distribuciones bimodales. Las diferencias entre las medidas ocurren con distribuciones sesgadas. La figura\(\PageIndex{3}\) muestra la distribución de 642 puntajes en una prueba introductoria de psicología. Observe que esta distribución tiene un ligero sesgo positivo.
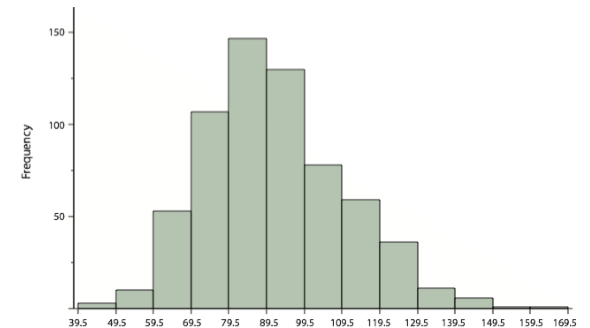
Las medidas de tendencia central se muestran en la Tabla\(\PageIndex{3}\). Observe que no difieren mucho, con la excepción de que el modo es considerablemente menor que las otras medidas. Cuando las distribuciones tienen un sesgo positivo, la media suele ser mayor que la mediana, aunque puede no estar en distribuciones bimodales. Para estos datos, la media de 91.58 es mayor que la mediana de 90. Este patrón se mantiene cierto para cualquier sesgo: el modo permanecerá en el punto más alto de la distribución, la mediana se sacará ligeramente hacia la cola sesgada (el extremo más largo de la distribución), y la media se sacará más lejos. Por lo tanto, la media es más sensible al sesgo que la mediana o modo, y en casos de sesgo extremo, la media puede que ya no sea apropiada para usar.
| Medir | Valor |
|---|---|
| Modo | 84.00 |
| Mediana | 90.00 |
| Media | 91.58 |
La distribución de los salarios del béisbol (en 1994) que se muestra en la Figura\(\PageIndex{4}\) tiene un sesgo mucho más pronunciado que la distribución en la Figura\(\PageIndex{3}\).
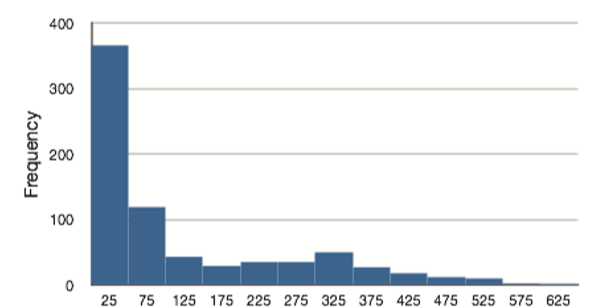
En el cuadro se\(\PageIndex{4}\) muestran las medidas de tendencia central para estos datos. El gran sesgo da como resultado valores muy diferentes para estas medidas. Ninguna medida única de tendencia central es suficiente para datos como estos. Si te hicieron la pregunta muy general: “Entonces, ¿qué hacen los beisbolistas?” y contestó con la media de 1.183.000 dólares, no habrías contado toda la historia ya que solo alrededor de un tercio de los beisbolistas ganan tanto. Si respondieras con la modalidad de 250.000 dólares o la mediana de 500.000 dólares, no estarías dando ninguna indicación de que algunos jugadores ganan muchos millones de dólares. Afortunadamente, no es necesario resumir una distribución con un solo número. Cuando las diversas medidas difieren, nuestra opinión es que se debe informar la media y la mediana. A veces también vale la pena reportar el modo. En los medios se suele reportar la mediana para resumir el centro de las distribuciones sesgadas. Escucharás sobre los salarios medios y los precios medios de las casas vendidas, etc. Esto es mejor que reportar solo la media, pero sería informativo escuchar más estadísticas.
| Medir | Valor |
|---|---|
| Modo | 250 |
| Mediana | 500 |
| Media | 1,183 |


