3.3: Difusión y Variabilidad
- Page ID
- 150689
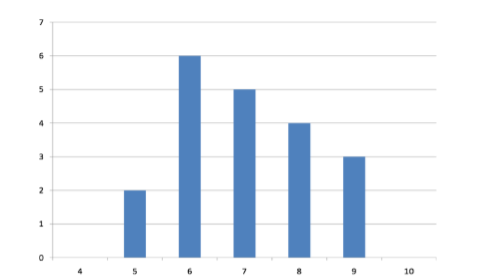
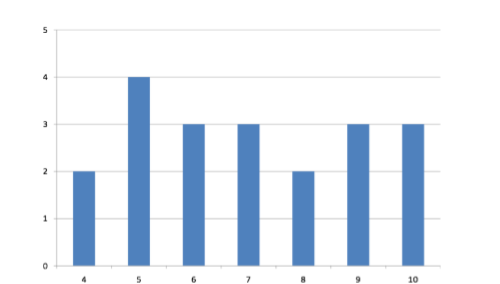
La variabilidad se refiere a lo “extendido” que está un grupo de puntajes. Para ver a qué nos referimos con spread out, considera gráficas en la Figura\(\PageIndex{1}\). Estas gráficas representan las puntuaciones en dos cuestionarios. La puntuación media para cada cuestionario es de 7.0. A pesar de la igualdad de medios, se puede ver que las distribuciones son bastante diferentes. Específicamente, las puntuaciones del Quiz 1 están más densamente empaquetadas y las del Quiz 2 están más extendidas. Las diferencias entre los estudiantes fueron mucho mayores en el Quiz 2 que en el Quiz 1.
Los términos variabilidad, dispersión y dispersión son sinónimos, y se refieren a cómo se extiende una distribución. Así como en la sección sobre tendencia central donde discutimos medidas del centro de una distribución de puntajes, en este capítulo discutiremos medidas de la variabilidad de una distribución. Existen tres medidas de variabilidad de uso frecuente: rango, varianza y desviación estándar. En los próximos párrafos, veremos cada una de estas medidas de variabilidad con más detalle.
Rango
El rango es la medida de variabilidad más simple de calcular, y una que probablemente hayas encontrado muchas veces en tu vida. El rango es simplemente el puntaje más alto menos el puntaje más bajo. Tomemos algunos ejemplos. ¿Cuál es el rango del siguiente grupo de números: 10, 2, 5, 6, 7, 3, 4? Bueno, el número más alto es 10, y el número más bajo es 2, por lo que 10 - 2 = 8. El rango es de 8. Tomemos otro ejemplo. Aquí hay un conjunto de datos con 10 números: 99, 45, 23, 67, 45, 91, 82, 78, 62, 51. ¿Cuál es el rango? El número más alto es 99 y el número más bajo es 23, por lo que 99 - 23 es igual a 76; el rango es 76. Consideremos ahora los dos cuestionarios que se muestran en Figura\(\PageIndex{1}\) y Figura\(\PageIndex{2}\). En el Quiz 1, la puntuación más baja es 5 y la puntuación más alta es 9. Por lo tanto, el rango es 4. El rango en el Quiz 2 fue mayor: la puntuación más baja fue 4 y la puntuación más alta fue 10. Por lo tanto el rango es de 6.
El problema con el uso de rango es que es extremadamente sensible a los valores atípicos, y un número lejos del resto de los datos alterará en gran medida el valor del rango. Por ejemplo, en el conjunto de números 1, 3, 4, 4, 5, 8 y 9, el rango es 8 (9 — 1).
No obstante, si sumamos una sola persona cuya puntuación no está ni cerca del resto de las puntuaciones, digamos, 20, el rango más que duplica del 8 al 19.
Gama Intercuartil
El rango intercuartil (IQR) es el rango del 50% medio de las puntuaciones en una distribución y a veces se usa para comunicar dónde se encuentra la mayor parte de los datos en la distribución. Se calcula de la siguiente manera:
\[\text {IQR} = 75\text {th percentile }- 25\text {th percentile}\]
Para el Quiz 1, el percentil 75 es 8 y el percentil 25 es 6. El rango intercuartílico es, por lo tanto, 2. Para el Quiz 2, que tiene mayor difusión, el percentil 75 es 9, el percentil 25 es 5 y el rango intercuartil es 4. Recordemos que en la discusión de las parcelas de caja, el percentil 75 se llamó la bisagra superior y el percentil 25 se llamó la bisagra inferior. Usando esta terminología, el rango intercuartílico se conoce como el H-spread.
Suma de Cuadrados
La variabilidad también se puede definir en términos de cuán cerca están las puntuaciones en la distribución a la mitad de la distribución. Usando la media como la medida de la mitad de la distribución, podemos ver qué tan lejos, en promedio, está cada punto de datos del centro. Los datos del Quiz 1 se muestran en la Tabla\(\PageIndex{1}\). La puntuación media es 7.0 (\(\Sigma \mathrm{X} / \mathrm{N}= 140/20 = 7\)). Por lo tanto, la columna “\(X-\overline {X}\)” contiene desviaciones (hasta qué punto se desvía cada puntaje de la media), aquí calculadas como la puntuación menos 7. La columna “\((X-\overline {X})^{2}\)” tiene las “Desviaciones Cuadradas” y es simplemente la columna anterior al cuadrado.
Hay algunas cosas a tener en cuenta sobre cómo\(\PageIndex{1}\) se formatea Table, ya que este es el formato que usarás para calcular la varianza (y, pronto, la desviación estándar). Las puntuaciones de datos brutos (\(\mathrm{X}\)) siempre se colocan en la columna más a la izquierda. Esta columna se suma luego en la parte inferior para facilitar el cálculo de la media (simplemente se divide este número por el número de puntuaciones en la tabla). Una vez que tengas la media, puedes trabajar fácilmente por la columna media calculando las puntuaciones de desviación. Esta columna también se suma y tiene una propiedad muy importante: siempre sumará a 0 (o cerca de cero si tiene error de redondeo debido a muchos decimales). Este paso se usa como un control de tus matemáticas para asegurarte de que no has cometido un error. Si esta columna suma a 0, puede pasar a rellenar la tercera columna de desviaciones cuadradas. Esta columna también se suma y tiene su propio nombre: la Suma de Cuadrados (abreviada como\(SS\) y dada la fórmula\(∑(X-\overline {X})^{2}\)). Como veremos, la Suma de Cuadrados aparece una y otra vez en diferentes fórmulas —es un valor muy importante, y esta tabla hace que sea sencillo de calcular sin error.
| \(\mathrm{X}\) | \(X-\overline{X}\) | \((X-\overline {X})^{2}\) |
|---|---|---|
| \ (\ mathrm {X}\) ">9 | \ (X-\ overline {X}\) ">2 | \ ((X-\ overline {X}) ^ {2}\) ">4 |
| \ (\ mathrm {X}\) ">9 | \ (X-\ overline {X}\) ">2 | \ ((X-\ overline {X}) ^ {2}\) ">4 |
| \ (\ mathrm {X}\) ">9 | \ (X-\ overline {X}\) ">2 | \ ((X-\ overline {X}) ^ {2}\) ">4 |
| \ (\ mathrm {X}\) ">8 | \ (X-\ overline {X}\) ">1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">8 | \ (X-\ overline {X}\) ">1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">8 | \ (X-\ overline {X}\) ">1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">8 | \ (X-\ overline {X}\) ">1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">7 | \ (X-\ overline {X}\) ">0 | \ ((X-\ overline {X}) ^ {2}\) ">0 |
| \ (\ mathrm {X}\) ">7 | \ (X-\ overline {X}\) ">0 | \ ((X-\ overline {X}) ^ {2}\) ">0 |
| \ (\ mathrm {X}\) ">7 | \ (X-\ overline {X}\) ">0 | \ ((X-\ overline {X}) ^ {2}\) ">0 |
| \ (\ mathrm {X}\) ">7 | \ (X-\ overline {X}\) ">0 | \ ((X-\ overline {X}) ^ {2}\) ">0 |
| \ (\ mathrm {X}\) ">7 | \ (X-\ overline {X}\) ">0 | \ ((X-\ overline {X}) ^ {2}\) ">0 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">6 | \ (X-\ overline {X}\) ">-1 | \ ((X-\ overline {X}) ^ {2}\) ">1 |
| \ (\ mathrm {X}\) ">5 | \ (X-\ overline {X}\) ">-2 | \ ((X-\ overline {X}) ^ {2}\) ">4 |
| \ (\ mathrm {X}\) ">5 | \ (X-\ overline {X}\) ">-2 | \ ((X-\ overline {X}) ^ {2}\) ">4 |
| \ (\ mathrm {X}\) ">\(\Sigma = 140\) | \ (X-\ overline {X}\) ">\(\Sigma = 0\) | \ ((X-\ overline {X}) ^ {2}\) ">\(\Sigma = 30\) |
Varianza
Ahora que tenemos calculada la Suma de Cuadrados, podemos usarla para calcular nuestra medida formal de distancia promedio desde la media, la varianza. La varianza se define como la diferencia cuadrática promedio de las puntuaciones con respecto a la media. Cuadramos las puntuaciones de desviación porque, como vimos en la tabla Suma de Cuadrados, la suma de las desviaciones brutas siempre es 0, y no hay nada que podamos hacer matemáticamente sin cambiar eso.
El parámetro poblacional para varianza es\(σ^2\) (“sigma-cuadrado”) y se calcula como:
\[\sigma^{2}=\dfrac{\sum(X-\mu)^{2}}{N} \]
Observe que el numerador esa fórmula es idéntica a la fórmula para Suma de Cuadrados presentada anteriormente con\(\overline {X}\) reemplazado por\(μ\). Así, podemos usar la tabla Suma de Cuadrados para calcular fácilmente el numerador y luego simplemente dividir ese valor por\(N\) para obtener varianza. Si asumimos que los valores en Tabla\(\PageIndex{1}\) representan la población completa, entonces podemos tomar nuestro valor de Suma de Cuadrados y dividirlo por\(N\) para obtener nuestra varianza poblacional:
\[\sigma^{2}=\dfrac{30}{20}=1.5 \nonumber \]
Entonces, en promedio, los puntajes en esta población están a 1.5 unidades cuadradas de distancia de la media. Esta medida de propagación es mucho más robusta (término que utilizan los estadísticos para significar resilientes o resistentes a) valores atípicos que el rango, por lo que es un valor mucho más útil para calcular. Adicionalmente, como veremos en futuros capítulos, la varianza juega un papel central en la estadística inferencial.
El estadístico muestral utilizado para estimar la varianza es\(s^2\) (“s-cuadrado”):
\[s^{2}=\dfrac{\sum(X-\overline{X})^{2}}{N-1} \]
Esta fórmula es muy similar a la fórmula para la varianza poblacional con un cambio: ahora dividimos por\(N – 1\) en lugar de\(N\). El valor\(N – 1\) tiene un nombre especial: los grados de libertad (abreviados como\(df\)). No es necesario entender en profundidad qué son los grados de libertad (esencialmente dan cuenta del hecho de que tenemos que usar una estadística de muestra para estimar la media (\(\overline {X}\)) antes de estimar la varianza) para calcular la varianza, pero saber que el denominador se llama\(df\) proporciona una buena taquigrafía para la fórmula de varianza:\(SS/df\).
Volviendo a los valores en Tabla\(\PageIndex{1}\) y tratando esas puntuaciones como una muestra, podemos estimar la varianza de la muestra como:
\[s^{2}=\dfrac{30}{20-1}=1.58 \]
Observe que este valor es ligeramente mayor al que calculamos cuando asumimos que estos puntajes eran la población completa. Esto se debe a que nuestro valor en el denominador es ligeramente menor, haciendo que el valor final sea más grande. En general, a medida que el tamaño\(N\) de tu muestra aumenta, el efecto de restar 1 se vuelve cada vez menos. Comparando un tamaño de muestra de 10 con un tamaño de muestra de 1000; 10 — 1 = 9, o 90% del valor original, mientras que 1000 — 1 = 999, o 99.9% del valor original. Así, tamaños de muestra más grandes acercarán la estimación de la varianza muestral a la varianza poblacional. Esta es una idea y principio clave en las estadísticas que veremos una y otra vez: los tamaños de muestra más grandes reflejan mejor la población.
Desviación estándar
La desviación estándar es simplemente la raíz cuadrada de la varianza. Esta es una estadística útil e interpretable porque tomar la raíz cuadrada de la varianza (recordando que la varianza es la diferencia cuadrada promedio) devuelve la desviación estándar a las unidades originales de la medida que usamos. Así, al reportar estadísticas descriptivas en un estudio, los científicos prácticamente siempre reportan la media y la desviación estándar. Por lo tanto, la desviación estándar es la medida de propagación más utilizada para nuestros fines.
El parámetro poblacional para la desviación estándar es\(σ\) (“sigma”), que, intuitivamente, es la raíz cuadrada del parámetro de varianza\(σ^2\) (en ocasiones, los símbolos funcionan muy bien de esa manera). La fórmula es simplemente la fórmula para la varianza bajo un signo de raíz cuadrada:
\[\sigma=\sqrt{\dfrac{\sum(X-\mu)^{2}}{N}} \]
Volver a nuestro ejemplo anterior de Table\(\PageIndex{1}\):
\[\sigma=\sqrt{\dfrac{30}{20}}=\sqrt{1.5}=1.22 \nonumber \]
El estadístico muestral sigue las mismas convenciones y se da como\(s\):
\[s=\sqrt{\dfrac{\sum(X-\overline {X})^{2}}{N-1}}=\sqrt{\dfrac{S S}{d f}} \]
La desviación estándar de la muestra de la Tabla\(\PageIndex{1}\) es:
\[s=\sqrt{\dfrac{30}{20-1}}=\sqrt{1.58}=1.26 \nonumber \]
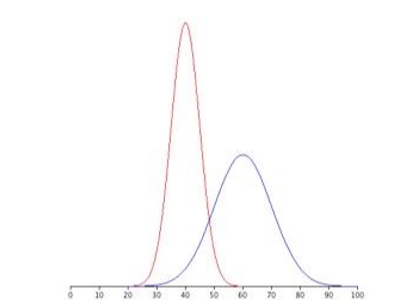
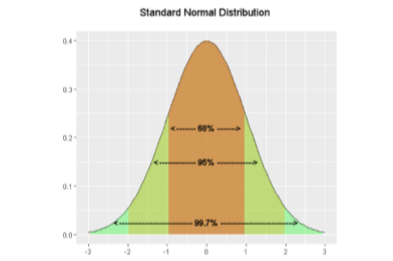
La desviación estándar es una medida especialmente útil de variabilidad cuando la distribución es normal o aproximadamente normal porque se puede calcular la proporción de la distribución dentro de un número dado de desviaciones estándar de la media. Por ejemplo, 68% de la distribución está dentro de una desviación estándar (arriba y abajo) de la media y aproximadamente 95% de la distribución está dentro de dos desviaciones estándar de la media. Por lo tanto, si tuvieras una distribución normal con una media de 50 y una desviación estándar de 10, entonces 68% de la distribución estaría entre 50 - 10 = 40 y 50 +10 =60. De igual manera, alrededor del 95% de la distribución estaría entre 50 - 2 x 10 = 30 y 50 + 2 x 10 = 70.
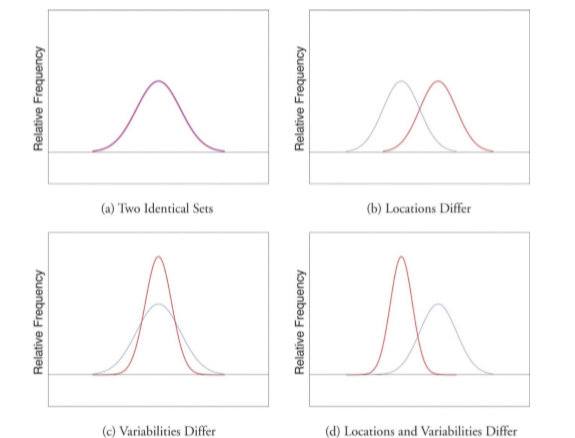
La figura\(\PageIndex{4}\) muestra dos distribuciones normales. La distribución roja tiene una media de 40 y una desviación estándar de 5; la distribución azul tiene una media de 60 y una desviación estándar de 10. Para la distribución roja, 68% de la distribución está entre 45 y 55; para la distribución azul, 68% está entre 50 y 70. Observe que a medida que la desviación estándar se hace más pequeña, la distribución se vuelve mucho más estrecha, independientemente de dónde se encuentre el centro de la distribución (media). La figura\(\PageIndex{5}\) presenta varios ejemplos más de este efecto.