7.5: Valores críticos, valores p y nivel de significancia

Un valor de probabilidad bajo arroja dudas sobre la hipótesis nula. ¿Qué tan bajo debe ser el valor de probabilidad para concluir que la hipótesis nula es falsa? Aunque claramente no hay una respuesta correcta o incorrecta a esta pregunta, es convencional concluir que la hipótesis nula es falsa si el valor de probabilidad es menor a 0.05. Investigadores más conservadores concluyen que la hipótesis nula es falsa solo si el valor de probabilidad es menor a 0.01. Cuando un investigador concluye que la hipótesis nula es falsa, se dice que el investigador rechazó la hipótesis nula. El valor de probabilidad por debajo del cual se rechaza la hipótesis nula se denomina nivel α o simplemente\(α\) (“alfa”). También se le llama el nivel de significancia. Si α no se especifica explícitamente, asuma que\(α\) = 0.05.

El nivel de significancia es un umbral que establecemos antes de recolectar datos para determinar si debemos o no rechazar la hipótesis nula. Establecimos este valor de antemano para evitar sesgarnos viendo nuestros resultados y luego determinando qué criterios debemos usar. Si nuestros datos producen valores que cumplen o superan este umbral, entonces tenemos evidencia suficiente para rechazar la hipótesis nula; si no, fallamos en rechazar el nulo (nunca “aceptamos” el nulo).

Hay dos criterios que utilizamos para evaluar si nuestros datos cumplen con los umbrales establecidos por nuestro nivel de significancia elegido, y ambos tienen que ver con nuestras discusiones de probabilidad y distribuciones. Recordemos que la probabilidad se refiere a la probabilidad de un evento, dada alguna situación o conjunto de condiciones. En las pruebas de hipótesis, esa situación es la suposición de que el valor de hipótesis nulo es el valor correcto, o que no hay efecto. El valor establecido en H0 es nuestra condición bajo la cual interpretamos nuestros resultados. Para rechazar esta suposición, y con ello rechazar la hipótesis nula, necesitamos resultados que serían muy improbables si el nulo fuera cierto. Ahora recordemos que los valores de z que caen en las colas de la distribución normal estándar representan valores poco probables. Es decir, la proporción del área bajo la curva como o más extrema que\(z\) es muy pequeña a medida que nos metemos en las colas de la distribución. Nuestro nivel de significancia corresponde al área bajo la cola que es exactamente igual a α: si usamos nuestro criterio normal de\(α\) = .05, entonces el 5% del área bajo la curva se convierte en lo que llamamos la región de rechazo (también llamada región crítica) de la distribución. Esto se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La región de rechazo para una prueba de una cola.

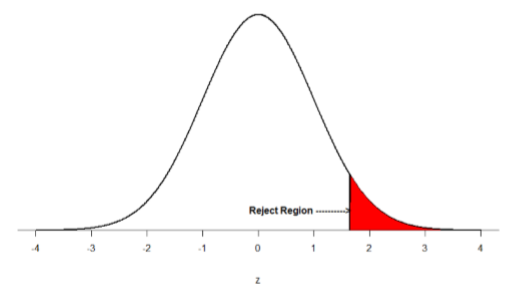
La región de rechazo sombreada nos lleva el 5% del área bajo la curva. Cualquier resultado que caiga en esa región es evidencia suficiente para rechazar la hipótesis nula.

La región de rechazo está delimitada por un\(z\) valor específico, al igual que cualquier área bajo la curva. En las pruebas de hipótesis, el valor correspondiente a una región de rechazo específica se denomina valor crítico,\(z_{crit}\) (“\(z\)-crit”) o\(z*\) (de ahí el otro nombre “región crítica”). Encontrar el valor crítico funciona exactamente igual que encontrar la puntuación z correspondiente a cualquier área bajo la curva como hicimos en la Unidad 1. Si vamos a la tabla normal, encontraremos que la puntuación z correspondiente al 5% del área bajo la curva es igual a 1.645 (\(z\)= 1.64 corresponde a 0.0405 y\(z\) = 1.65 corresponde a 0.0495, así que .05 está exactamente entre ellas) si vamos a la derecha y -1.645 si vamos a la izquierda. La dirección debe estar determinada por su hipótesis alternativa, y dibujar luego sombrear la distribución es útil para mantener la direccionalidad recta.

Supongamos, sin embargo, que queremos hacer una prueba no direccional. Tenemos que poner la región crítica en ambas colas, pero no queremos aumentar el tamaño general de la región de rechazo (por razones que veremos más adelante). Para ello, simplemente lo dividimos por la mitad para que una proporción igual del área bajo la curva caiga en la región de rechazo de cada cola. Para\(α\) = .05, esto significa que 2.5% del área está en cada cola, la cual, con base en la tabla z, corresponde a valores críticos de\(z*\) = ±1.96. Esto se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Región de rechazo de dos colas.

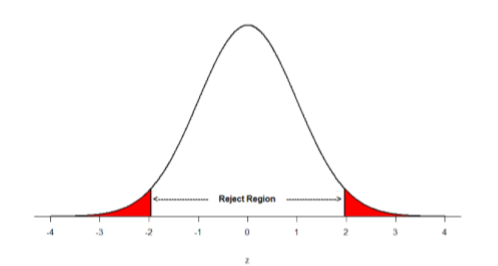
Así, cualquier\(z\) -score que caiga fuera de ±1.96 (mayor a 1.96 en valor absoluto) cae en la región de rechazo. Cuando usamos\(z\) -scores de esta manera, el valor obtenido de\(z\) (a veces llamado\(z\) -obtenido) es algo conocido como estadística de prueba, que es simplemente una estadística inferencial utilizada para probar una hipótesis nula. La fórmula para nuestra\(z\) estadística no ha cambiado:

\[z=\dfrac{\overline{\mathrm{X}}-\mu}{\bar{\sigma} / \sqrt{\mathrm{n}}} \]

Para probar formalmente nuestra hipótesis, comparamos nuestro\(z\) estadístico obtenido con nuestro\(z\) valor crítico. Si\(\mathrm{Z}_{\mathrm{obt}}>\mathrm{Z}_{\mathrm{crit}}\), eso significa que cae en la región de rechazo (para ver por qué, trazar una línea para\(z\) = 2.5 en Figura\(\PageIndex{1}\) o Figura\(\PageIndex{2}\)) y así rechazamos\(H_0\). Si\(\mathrm{Z}_{\mathrm{obt}}<\mathrm{Z}_{\mathrm{crit}}\), no lo rechazamos. Recuerde que a medida que\(z\) se hace más grande, el área correspondiente bajo la curva más allá\(z\) se hace más pequeña. Así, la proporción, o\(p\) -valor, será menor que el área para\(α\), y si el área es menor, la probabilidad se vuelve más pequeña. Específicamente, la probabilidad de obtener ese resultado, o un resultado más extremo, bajo la condición de que la hipótesis nula sea verdadera se hace menor.

El\(z\) -estadístico es muy útil cuando estamos haciendo nuestros cálculos a mano. Sin embargo, cuando usamos software de computadora, nos reportará un\(p\) -valor, que es simplemente la proporción del área bajo la curva en las colas más allá de nuestra\(z\) estadística obtenida. Podemos comparar directamente este\(p\) -valor\(α\) para probar nuestra hipótesis nula: si\(p < α\), rechazamos\(H_0\), pero si\(p > α\), fallamos en rechazar. Obsérvese también que lo contrario siempre es cierto: si utilizamos valores críticos para probar nuestra hipótesis, siempre sabremos si\(p\) es mayor o menor que\(α\). Si rechazamos, sabemos que\(p < α\) debido a que el\(z\) -estadístico obtenido cae más lejos en la cola que el\(z\) -valor crítico que corresponde a\(α\), por lo que la proporción (\(p\)-valor) para ese\(z\) -estadístico será menor. Por el contrario, si no rechazamos, sabemos que la proporción será mayor que\(α\) porque el\(z\) -estadístico no estará tan lejos en la cola. Esto se ilustra para una prueba de una cola en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Relación entre\(α\),\(z_{obt}\), y\(p\)

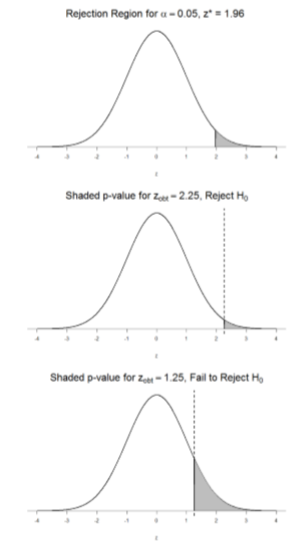
Cuando se rechaza la hipótesis nula, se dice que el efecto es estadísticamente significativo. Por ejemplo, en el estudio de caso Physicians Reacciones, el valor de probabilidad es 0.0057. Por lo tanto, el efecto de la obesidad es estadísticamente significativo y se rechaza la hipótesis nula de que la obesidad no hace diferencia. Es muy importante tener en cuenta que la significancia estadística significa sólo que se rechaza la hipótesis nula de exactamente ningún efecto; no significa que el efecto sea importante, que es lo que generalmente significa “significativo”. Cuando un efecto es significativo, puedes tener confianza en que el efecto no es exactamente cero. Encontrar que un efecto es significativo no te dice qué tan grande o importante es el efecto. No confundir la significación estadística con la significación práctica. Un pequeño efecto puede ser muy significativo si el tamaño de la muestra es lo suficientemente grande. ¿Por qué la palabra “significativo” en la frase “estadísticamente significativo” significa algo tan diferente de otros usos de la palabra? Curiosamente, esto se debe a que el significado de “significativo” en el lenguaje cotidiano ha cambiado. Resulta que cuando se desarrollaron los procedimientos para la prueba de hipótesis, algo era “significativo” si significaba algo. Así, encontrar que un efecto es estadísticamente significativo significa que el efecto es real y no por casualidad. A lo largo de los años, el significado de “significativo” cambió, lo que llevó a la posible mala interpretación.