3.10: Comparar medidas
- Page ID
- 152287
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Exponer en qué se diferencian las medidas en las distribuciones simétricas
- Determine qué medida (es) debe (n) ser utilizada (s) para describir el centro de una distribución sesgada
¿Cómo se comparan entre sí las diversas medidas de tendencia central? Para las distribuciones simétricas, la media, la mediana, la trimedia y la media recortada son iguales, al igual que el modo excepto en distribuciones bimodales. Las diferencias entre las medidas ocurren con distribuciones sesgadas. La figura\(\PageIndex{1}\) muestra la distribución de las\(642\) puntuaciones en una prueba introductoria de psicología. Observe que esta distribución tiene un ligero sesgo positivo.
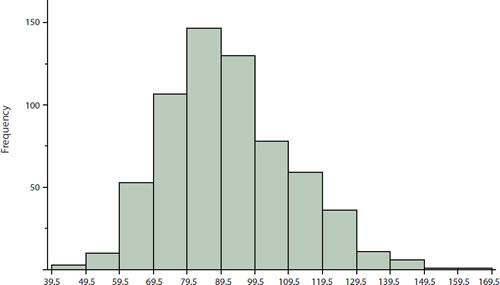
Las medidas de tendencia central se muestran en la Tabla\(\PageIndex{1}\). Observe que no difieren mucho, con la excepción de que el modo es considerablemente menor que las otras medidas. Cuando las distribuciones tienen un sesgo positivo, la media suele ser mayor que la mediana, aunque puede no estar en distribuciones bimodales. Para estos datos, la media de\(91.58\) es mayor que la mediana de\(90\). Por lo general, la media trimedia y recortada caerán entre la mediana y la media, aunque en este caso, la media recortada es ligeramente inferior a la mediana. La media geométrica es menor que todas las medidas excepto el modo.
| Medir | Valor |
|---|---|
| Modo | 84.00 |
| Mediana | 90.00 |
| Media Geométrica | 89.70 |
| Trimean | 90.25 |
| Media recortada 50% | 89.81 |
| Media | 91.58 |
La distribución de los salarios del béisbol (in\(1994\)) que se muestra en la Figura\(\PageIndex{2}\) tiene un sesgo mucho más pronunciado que la distribución en la Figura\(\PageIndex{2}\).
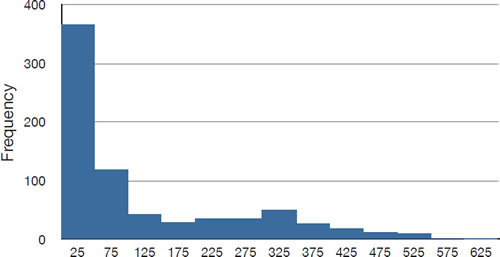
En el cuadro se\(\PageIndex{2}\) muestran las medidas de tendencia central para estos datos. El gran sesgo da como resultado valores muy diferentes para estas medidas. Ninguna medida única de tendencia central es suficiente para datos como estos. Si te hicieron la pregunta muy general: “Entonces, ¿qué hacen los beisbolistas?” y respondió con la media de\(\$1,183,000\), no habrías contado toda la historia ya que solo alrededor de un tercio de los beisbolistas ganan tanto. Si respondieras con la modalidad de\(\$250,000\) o la mediana de\(\$500,000\), no estarías dando ninguna indicación de que algunos jugadores ganan muchos millones de dólares. Afortunadamente, no hay necesidad de resumir una distribución con un solo número. Cuando las diversas medidas difieren, nuestra opinión es que se debe reportar la media, mediana, y ya sea la trimedia o la media recortada\(50\%\). A veces también vale la pena reportar el modo. En los medios se suele reportar la mediana para resumir el centro de las distribuciones sesgadas. Escucharás sobre los salarios medios y los precios medios de las casas vendidas, etc. Esto es mejor que reportar solo la media, pero sería informativo escuchar más estadísticas.
| Medir | Valor |
|---|---|
| Modo | 250 |
| M edian | 500 |
| Media Geométrica | 555 |
| Trimean | 792 |
| Mea n Recorte 50% | 619 |
| Media | 1,183 |


