7.6: Aproximación normal al binomio

Última actualización
Guardar como PDF

Page ID: 152266

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Indicar la relación entre la distribución normal y la distribución binomial
Utilizar la distribución normal para aproximar la distribución binomial
Estado cuando la aproximación es adecuada

En la sección sobre la historia de la distribución normal, vimos que la distribución normal puede ser utilizada para aproximar la distribución binomial. En esta sección se muestra cómo calcular estas aproximaciones.

Empecemos con un ejemplo. Suponga que tiene una moneda justa y desea saber la probabilidad de que obtenga\(8\) cabezas de\(10\) volteretas. La distribución binomial tiene una media de\(\mu =N\pi =(10)(0.5)=5\) y una varianza de\(\sigma ^2=N\pi (1-\pi )=(10)(0.5)(0.5)=2.5\). Por lo tanto, la desviación estándar es\(1.5811\). Un total de\(8\) cabezas es desviaciones\((8 - 5)/1.5811 = 1.897\) estándar por encima de la media de la distribución. La pregunta entonces es: “¿Cuál es la probabilidad de obtener un valor exactamente desviaciones\(1.897\) estándar por encima de la media?” Te puede sorprender saber que la respuesta es\(0\): La probabilidad de que algún punto específico sea\(0\). El problema es que la distribución binomial es una distribución de probabilidad discreta, mientras que la distribución normal es una distribución continua.

La solución es redondear y considerar cualquier valor de\(7.5\)\(8.5\) a para representar un resultado de\(8\) cabezas. Usando este enfoque, calculamos el área bajo una curva normal de\(7.5\) a\(8.5\). El área en verde en la Figura\(\PageIndex{1}\) es una aproximación de la probabilidad de obtener\(8\) cabezas.

Figura\(\PageIndex{1}\): *Aproximación a la probabilidad de\(8\) cabezas con la distribución normal.*

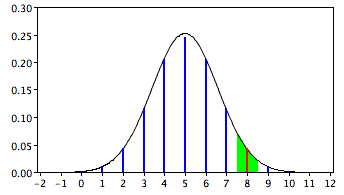
Por lo tanto, la solución es computar esta área. Primero calculamos el área de abajo\(8.5\) y luego restamos el área de abajo\(7.5\).

Los resultados del uso de la calculadora de área normal para encontrar el área a continuación se\(8.5\) muestran en la Figura\(\PageIndex{2}\). Los resultados para\(7.5\) se muestran en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{2}\): Área abajo\(8.5\)

Figura\(\PageIndex{3}\): Área abajo\(7.5\)

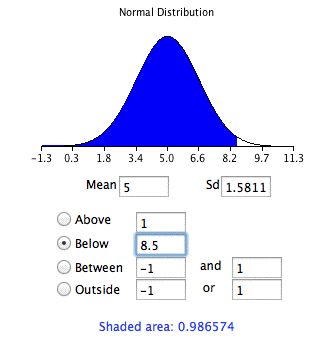
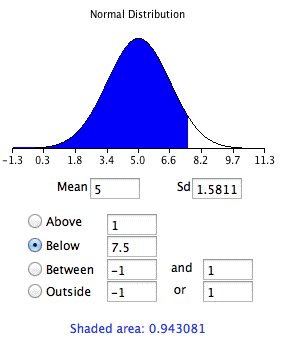
La diferencia entre las áreas es\(0.044\), que es la aproximación de la probabilidad binomial. Para estos parámetros, la aproximación es muy precisa. La demostración en la siguiente sección le permite explorar su precisión con diferentes parámetros.

Si no tenía la calculadora de área normal, podría encontrar la solución usando una tabla de la distribución normal estándar (una\(Z\) tabla) de la siguiente manera:

Encuentra una\(Z\) puntuación para\(8.5\) usar la fórmula\(Z = (8.5 - 5)/1.5811 = 2.21\).
Encuentra el área debajo\(Z\) de una de\(2.21 = 0.987\).
Encuentra una\(Z\) puntuación para\(7.5\) usar la fórmula\(Z = (7.5 - 5)/1.5811 = 1.58\).
Encuentra el área debajo\(Z\) de una de\(1.58 = 0.943\).
Restar el valor en paso\(4\) del valor en paso\(2\) para obtener\(0.044\).

La misma lógica se aplica al calcular la probabilidad de un rango de resultados. Por ejemplo, para calcular la probabilidad de\(8\)\(10\) voltear, calcular el área de\(7.5\) a\(10.5\).

La precisión de la aproximación depende de los valores de\(N\) y\(\pi\). Una regla general es que la aproximación es buena si ambos\(N\pi\) y ambos\(N(1-\pi )\) son mayores que\(10\).