10.E: Estimación (Ejercicios)
- Page ID
- 151983
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Es posible que desee utilizar el Laboratorio de Análisis y varias calculadoras para algunos de estos ejercicios.
Calculadoras:
- Distribución t inversa: Encuentra t para un intervalo de confianza.
- t Distribución: Computa áreas de la distribución t.
- Fisher's r a z': Calcula transformaciones en ambas direcciones.
- Distribución Normal Inversa: Utilizar para intervalos de confianza.
Preguntas Generales
Q1
¿Cuándo se consideraría estadística la nota media en una clase en un examen final? ¿Cuándo se consideraría un parámetro? (sección pertinente)
Q2
Definir sesgo en términos de valor esperado. (sección pertinente)
Q3
¿Es posible que una estadística sea imparcial pero muy imprecisa? ¿Qué tal ser muy preciso pero sesgado? (sección pertinente)
Q4
¿Por qué un intervalo de\(99\%\) confianza es más amplio que un intervalo de\(95\%\) confianza? (sección relevante y sección relevante)
Q5
Cuando construes un intervalo de\(95\%\) confianza, ¿en qué\(95\%\) confías? (sección pertinente)
Q6
¿Cuál es la diferencia en el cálculo de un intervalo de confianza entre los casos en los que se conoce la desviación estándar de la población y los casos en los que hay que estimarla? (sección relevante y sección relevante)
Q7
Supongamos que un investigador encontró que la correlación entre una prueba que él o ella desarrolló y el desempeño laboral estaba\(0.55\) en un estudio de\(28\) empleados. Si las correlaciones bajo\(0.35\) se consideran inaceptables, ¿tendría alguna reserva sobre el uso de esta prueba para seleccionar a los solicitantes de empleo? (sección pertinente)
Q8
¿Cuál es el efecto del tamaño de la muestra en el ancho de un intervalo de confianza? (sección relevante y sección relevante)
Q9
¿Cómo se compara la\(t\) distribución con la distribución normal? ¿Cómo afecta esta diferencia al tamaño de los intervalos de confianza construidos usando\(z\) respecto a los construidos usando\(t\)? ¿El tamaño de la muestra hace la diferencia? (sección pertinente)
Q10
Se está investigando la efectividad de un medicamento para la presión arterial. ¿Cómo podría un experimentador demostrar que, en promedio, la reducción de la presión arterial sistólica es\(20\) o mayor? (sección relevante y sección relevante)
Q11
Se sabe que una población se distribuye normalmente con una desviación estándar de\(2.8\).
- Calcular el intervalo de\(95\%\) confianza sobre la media con base en la siguiente muestra de nueve:\(8, 9, 10, 13, 14, 16, 17, 20, 21\).
- Ahora calcula el intervalo de\(99\%\) confianza usando los mismos datos. (sección pertinente)
Q12
Una persona afirma ser capaz de predecir el resultado de voltear una moneda. Esta persona es\(16/25\) tiempos correctos. Calcular el intervalo de\(95\%\) confianza en la proporción de veces que esta persona puede predecir los volteos de monedas correctamente. ¿Qué conclusión puedes sacar sobre esta prueba de su capacidad para predecir el futuro? (sección pertinente)
Q13
¿Qué significa que la varianza (calculada dividiendo por\(N\)) es una estadística sesgada? (sección pertinente)
Q14
Un intervalo de confianza para la media poblacional computada a partir\(N\) de una de\(16\) rangos de\(12\) a\(28\). Se va a tomar una nueva muestra de\(36\) observaciones. No se puede saber de antemano exactamente cuál será el intervalo de confianza porque depende de la muestra aleatoria. Aun así, deberías tener alguna idea de lo que va a ser. Da tu mejor estimación. (sección pertinente)
Q15
Se toma una muestra de\(22\) una población de puntajes de exámenes, y la media de su muestra es\(60\).
- Sabes que la desviación estándar de la población es\(10\). Cuál es el intervalo de\(99\%\) confianza en la población media.
- Ahora suponga que no conoce la desviación estándar de la población, pero la desviación estándar en su muestra lo es\(10\). ¿Cuál es el intervalo de\(99\%\) confianza en la media ahora? (sección pertinente)
Q16
Lees sobre una encuesta en un periódico y encuentras que\(70\%\) de las\(250\) personas muestreadas prefieren Candidato\(A\). Te sorprende esta encuesta porque pensaste que más como\(50\%\) de la población prefería a este candidato. A partir de esta muestra, ¿es posible\(50\%\) una proporción poblacional? Compute el intervalo de\(95\%\) confianza para estar seguro. (sección pertinente)
Q17
Se calcularon las alturas para adolescentes varones y niñas. La estatura media para la muestra de\(12\) niños fue\(174\) cm y la varianza fue\(62\). Para la muestra de\(12\) niñas, la media fue\(166\) cm y la varianza fue\(65\).
- ¿Cuál es el intervalo de\(95\%\) confianza sobre la diferencia entre medias poblacionales?
- ¿Cuál es el intervalo de\(99\%\) confianza sobre la diferencia entre medias poblacionales?
- ¿Crees que la diferencia media en la población podría ser sobre\(5\)? ¿Por qué o por qué no? (sección pertinente)
Q18
Te interesó cuánto tiempo estudia la especialización en psicología promedio en tu universidad por noche, así que pediste a las carreras de\(10\) psicología que te indicaran la cantidad que estudian. Te dijeron las siguientes veces:\(2, 1.5, 3, 2, 3.5, 1, 0.5, 3, 2, 4\).
- Encontrar el intervalo de\(95\%\) confianza en la media poblacional.
- Encontrar el intervalo de\(90\%\) confianza en la media poblacional. (sección pertinente)
Q19
Verdadero/falso: A medida que aumenta el tamaño de la muestra, aumenta la probabilidad de que el intervalo de confianza contenga la media poblacional. (sección relevante y sección relevante)
Q20
Verdadero/falso: Tienes una muestra de\(9\) hombres y una muestra de\(8\) mujeres. Los grados de libertad para el\(t\) valor en su intervalo de confianza sobre la diferencia entre medias es\(16\). (sección relevante y sección relevante)
Q21
Verdadero/falso: Las letras griegas se utilizan para las estadísticas a diferencia de los parámetros. (sección pertinente)
Q22
Verdadero/falso: Para construir un intervalo de confianza sobre la diferencia entre medias, es necesario asumir que las poblaciones tienen la misma varianza y ambas están distribuidas normalmente. (sección pertinente)
Q23
Verdadero/falso: La distribución roja representa la sección\(t\) distribution and the blue distribution represents the normal distribution. ( relevante)
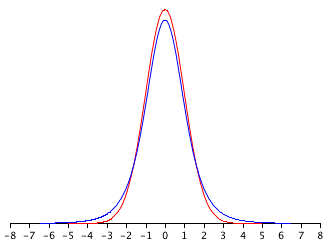
Preguntas de casos prácticos
Las siguientes preguntas son del estudio de caso Angry Moods (AM).
Q24
(AM #6c) ¿Hay alguna diferencia en cuanto hombres y mujeres usan el comportamiento agresivo para mejorar un estado de ánimo enojado? Para las puntuaciones de “Anger-Out”, computar un intervalo de\(99\%\) confianza sobre la diferencia entre medias de género. (sección pertinente)
Q25
(AM #10) Calcula el intervalo de\(95\%\) confianza para la diferencia entre la puntuación media de Anger-In para los atletas y los no atletas. ¿Qué puedes concluir? (sección pertinente)
Q26
Encuentra el intervalo de\(95\%\) confianza en la correlación poblacional entre las puntuaciones Anger-Out y Control-Out. (sección pertinente)
Las siguientes preguntas son del estudio de caso Flatulencia (F).
Q27
(F #8) Compara hombres y mujeres en la variable “perday”. Calcular el intervalo de\(95\%\) confianza sobre la diferencia entre medias. (sección pertinente)
Q28
(F #10) ¿Cuál es el intervalo de\(95\%\) confianza del tiempo medio que la gente espera antes de tirarse pedos frente a una pareja romántica? (sección pertinente)
Las siguientes preguntas utilizan datos del estudio de caso Animal Research (AR).
Q29
(AR #3) ¿Qué porcentaje de las mujeres estudiadas en esta muestra coincidieron firmemente (dieron una calificación de\(7\)) en que usar animales para la investigación es incorrecto?
Q30
Usa la proporción que calculaste en #29. Calcular el intervalo de\(95\%\) confianza en la proporción poblacional de mujeres que coinciden firmemente en que la investigación animal es incorrecta. (sección pertinente)
Q31
Calcular un intervalo de\(95\%\) confianza sobre la diferencia entre las medias de género con respecto a sus creencias de que la investigación animal es incorrecta. (sección pertinente)
La siguiente pregunta es del estudio de caso Tratamiento del TDAH (AT).
Q32
(AT #8) ¿Cuál es la correlación entre el número correcto de respuestas de los participantes después de tomar el placebo y su número correcto de respuestas después de tomar\(0.60\) mg/kg de MPH? Calcular el intervalo de\(95\%\) confianza en la correlación poblacional. (sección pertinente)
La siguiente pregunta es del estudio de caso Armas y Agresión (WA).
Q33
(WA #4) Recordemos que la hipótesis es que una persona puede nombrar una palabra agresiva más rápidamente si va precedida de una palabra arma primo que si va precedida de una palabra neutra prima. El primer paso para probar esta hipótesis es calcular la diferencia entre
- el tiempo de denominación de palabras agresivas cuando son precedidas por una palabra neutral prime y
- el tiempo de denominación de palabras agresivas cuando son precedidas por una palabra arma prima por separado para cada uno de los\(32\) participantes. Es decir, computar un\(- aw\) para cada participante.
- ¿Se apoyaría la hipótesis de este estudio si la diferencia fuera positiva o negativa?
- ¿Cuál es la media de esta puntuación de diferencia? (sección pertinente)
- ¿Cuál es la desviación estándar de esta puntuación de diferencia? (sección pertinente)
- ¿Cuál es el intervalo de confianza del 95% de la puntuación de diferencia media? (sección pertinente)
- Qué dice el intervalo de confianza calculado en (d) sobre la hipótesis.
La siguiente pregunta es del estudio de caso Dieta y Salud (WA).
Q34
Calcular un intervalo de\(95\%\) confianza sobre la proporción de personas sanas que siguen la dieta AHA.
| Cánceres | Muertes | Enfermedad no mortal | Saludable | Total | |
| AHA |
Las siguientes preguntas son de (reproducidas con permiso) Visitar el sitio
Visitar el sitio
Q35
Supongamos que toma una muestra aleatoria de\(10,000\) estadounidenses y encuentra que\(1,111\) son zurdos. Se realiza una prueba de significancia para evaluar si los datos de la muestra proporcionan evidencia\(10\%\) de que más de todos los estadounidenses son zurdos, y se calcula una estadística de prueba de\(3.70\) y un\(p\) valor de\(0.0001\). Además, se calcula un intervalo de\(99\%\) confianza para que sea la proporción de zurdos en Estados Unidos\((0.103,0.119)\). Considere las siguientes afirmaciones: La muestra proporciona pruebas contundentes de que más\(10\%\) de todos los estadounidenses son zurdos. La muestra proporciona evidencia de que la proporción de zurdos en América es mucho mayor que\(10\%\). ¿Cuál de estas dos afirmaciones es la conclusión más apropiada a sacar? Explica tu respuesta con base en los resultados de la prueba de significancia y el intervalo de confianza.
Q36
Un estudiante quería estudiar las edades de las parejas que solicitan licencias de matrimonio en su condado. Estudió una muestra de licencias de\(94\) matrimonio y encontró que en\(67\) los casos el esposo era mayor que la esposa. ¿Los datos de la muestra proporcionan evidencia contundente de que el esposo suele ser mayor que la esposa entre las parejas que solicitan licencias de matrimonio en ese condado? Explique brevemente y justifique su respuesta.
Q37
Imagínese que hay\(100\) diferentes investigadores cada uno estudiando los hábitos de sueño de los estudiantes universitarios de primer año. Cada investigador toma una muestra aleatoria de tamaño\(50\) de la misma población de estudiantes de primer año. Cada investigador está tratando de estimar la media de horas de sueño que los estudiantes de primer año obtienen por la noche, y cada uno construye un intervalo de\(95\%\) confianza para la media. Aproximadamente ¿cuántos de estos intervalos de\(100\) confianza NO capturarán la verdadera media?
- Ninguno
- \(1\)o\(2\)
- \(3\)a\(7\)
- alrededor de la mitad
- \(95\)a\(100\)
- otro
Respuestas Seleccionadas
S11
- \((12.39, 16.05)\)
S12
\((0.43, 0.85)\)
S15
- \((53.96, 66.04)\)
S17
- \((1.25, 14.75)\)
S18
- \((1.45, 3.05)\)
S26
\((-0.713, -0.414)\)
S27
\((-0.98, 3.09)\)
S29
\(41\%\)
S33
- \(7.16\)


