2.3: Histogramas, Polígonos de Frecuencia y Gráficas de Series de Tiempo
- Page ID
- 153258
Para la mayor parte del trabajo que realices en este libro, utilizarás un histograma para mostrar los datos. Una ventaja de un histograma es que puede mostrar fácilmente grandes conjuntos de datos. Una regla general es usar un histograma cuando el conjunto de datos consta de 100 valores o más.
Un histograma consiste en cajas contiguas (contiguas). Tiene tanto un eje horizontal como un eje vertical. El eje horizontal está etiquetado con lo que representan los datos (por ejemplo, la distancia de tu casa a la escuela). El eje vertical está etiquetado ya sea frecuencia o frecuencia relativa (o porcentaje de frecuencia o probabilidad). La gráfica tendrá la misma forma con cualquiera de las etiquetas. El histograma (como el stemplot) puede darle la forma de los datos, el centro y la dispersión de los datos.
La frecuencia relativa es igual a la frecuencia para un valor observado de los datos dividido por el número total de valores de datos en la muestra. (Recuerde, la frecuencia se define como el número de veces que ocurre una respuesta). Si:
- \(f\)es frecuencia
- \(n\)es el número total de valores de datos (o la suma de las frecuencias individuales), y
- \(RF\)es la frecuencia relativa,
entonces:
\[RF=\dfrac{f}{n} \label{2.3.1}\]
Por ejemplo, si tres alumnos de la clase de inglés del señor Ahab, de 40 alumnos, recibieron del 90% al 100%, entonces, f = 3, n = 40, y RF = fn = 340 = 0.075. El 7.5% de los estudiantes recibió 90— 100%. 90— 100% son medidas cuantitativas.
Para construir un histograma, primero decida cuántas barras o intervalos, también llamados clases, representan los datos. Muchos histogramas constan de cinco a 15 barras o clases para mayor claridad. Se debe elegir el número de barras. Elija un punto de partida para que el primer intervalo sea menor que el valor de datos más pequeño. Un punto de partida conveniente es un valor menor llevado a cabo a una posición decimal más que el valor con más decimales. Por ejemplo, si el valor con más decimales es 6.1 y este es el valor más pequeño, un punto de partida conveniente es\(6.05 (6.1 – 0.05 = 6.05)\). Decimos que 6.05 tiene más precisión. Si el valor con más decimales es 2.23 y el valor más bajo es 1.5, un punto de partida conveniente es\(1.495 (1.5 – 0.005 = 1.495)\). Si el valor con más decimales es 3.234 y el valor más bajo es 1.0, un punto de partida conveniente es\(0.9995 (1.0 – 0.0005 = 0.9995)\). Si todos los datos resultan ser enteros y el valor más pequeño es dos, entonces un punto de partida conveniente es\(1.5 (2 - 0.5 = 1.5)\). Además, cuando el punto de partida y otros límites se llevan a un decimal adicional, ningún valor de datos caerá sobre un límite. Los siguientes dos ejemplos entran en detalle sobre cómo construir un histograma usando datos continuos y cómo crear un histograma usando datos discretos.
Ejemplo\(\PageIndex{1}\)
Los siguientes datos son las alturas (en pulgadas a la media pulgada más cercana) de 100 futbolistas semiprofesionales masculinos. Las alturas son datos continuos, ya que se mide la altura.
60; 60.5; 61; 61; 61.5
63.5; 63.5; 63.5
64; 64; 64; 64; 64; 64; 64; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5
66; 66; 66; 66; 66; 66; 66; 66; 66; 66; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67.5
68; 68; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69.5; 69.5; 69.5; 69.5; 69.5; 69.5
70; 70; 70; 70; 70; 70; 70.5; 70.5; 70.5; 71; 71; 71
72; 72; 72; 72.5; 72.5; 73; 73.5
74
El valor de datos más pequeño es 60. Dado que los datos con más decimales tienen un decimal (por ejemplo, 61.5), queremos que nuestro punto de partida tenga dos decimales. Dado que los números 0.5, 0.05, 0.005, etc. son números convenientes, usa 0.05 y restarlo de 60, el valor más pequeño, para el punto de partida conveniente.
60 — 0.05 = 59.95 que es más preciso que, digamos, 61.5 por un decimal. El punto de partida es, entonces, 59.95.
El valor más grande es 74, por lo que 74 + 0.05 = 74.05 es el valor final.
A continuación, calcule el ancho de cada barra o intervalo de clase. Para calcular este ancho, resta el punto inicial del valor final y divídalo por el número de barras (debes elegir el número de barras que desees). Supongamos que eliges ocho barras.
\[\dfrac{74.05−59.95}{8}=1.76\]Redondearemos hasta dos y haremos que cada barra o intervalo de clase sea de dos unidades de ancho. Redondear hasta dos es una forma de evitar que un valor caiga sobre un límite. El redondeo al siguiente número suele ser necesario incluso si va en contra de las reglas estándar de redondeo. Para este ejemplo, usar 1.76 como ancho también funcionaría. Una pauta que es seguida por algunos para el ancho de una barra o intervalo de clase es tomar la raíz cuadrada del número de valores de datos y luego redondear al número entero más cercano, si es necesario. Por ejemplo, si hay 150 valores de datos, tomar la raíz cuadrada de 150 y redondear a 12 barras o intervalos.
Los límites son:
- 59.95
- 59.95 + 2 = 61.95
- 61.95 + 2 = 63.95
- 63.95 + 2 = 65.95
- 65.95 + 2 = 67.95
- 67.95 + 2 = 69.95
- 69.95 + 2 = 71.95
- 71.95 + 2 = 73.95
- 73.95 + 2 = 75.95
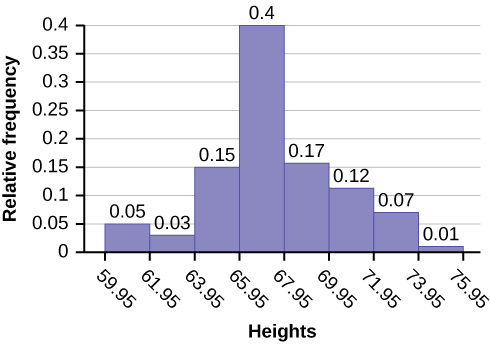
Las alturas de 60 a 61.5 pulgadas están en el intervalo 59.95—61.95. Las alturas que son 63.5 están en el intervalo 61.95—63.95. Las alturas que son de 64 a 64.5 están en el intervalo 63.95—65.95. Las alturas 66 a 67.5 están en el intervalo 65.95—67.95. Las alturas 68 a 69.5 están en el intervalo 67.95—69.95. Las alturas 70 a 71 están en el intervalo 69.95—71.95. Las alturas 72 a 73.5 están en el intervalo 71.95—73.95. La altura 74 está en el intervalo 73.95—75.95.
El siguiente histograma muestra las alturas en el eje x y la frecuencia relativa en el eje y.
Ejercicio\(\PageIndex{1}\)
Los siguientes datos son las tallas de zapatos de 50 estudiantes varones. Los tamaños son datos discretos ya que el tamaño del zapato se mide solo en unidades enteras y medias. Construir un histograma y calcular el ancho de cada barra o intervalo de clase. Supongamos que eliges seis barras.
9; 9; 9.5; 9.5; 10; 10; 10; 10; 10; 10.5; 10.5; 10.5; 10.5; 10.5; 10.5; 10.5; 10.5; 10.5 11; 11;
11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11.5; 11.5; 11.5; 11.5; 11.5; 11.5; 11.5; 11.5; 12; 12;
12; 12; 12; 12.5; 12.5; 12.5; 12.5; 12.5; 12.5; 12.5; 12.5; 12.5; 12.5; 14
Contestar
Valor más pequeño: 9
Valor más grande: 14
Valor inicial conveniente: 9 — 0.05 = 8.95
Valor final conveniente: 14 + 0.05 = 14.05
\(\frac{14.05-8.95}{6}\) = 0.85
Los cálculos sugieren usar 0.85 como el ancho de cada barra o intervalo de clase. También puedes usar un intervalo con un ancho igual a uno.
Ejemplo\(\PageIndex{2}\)
Los siguientes datos son el número de libros comprados por 50 estudiantes universitarios de medio tiempo en ABC College. El número de libros son datos discretos, ya que se cuentan los libros.
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2;
2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2;
2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2;
2; 2; 2; 2; 2; 2; 2; 2
; 2; 2; 2; 2; 2; 2; 2; 2
Once alumnos compran un libro. Diez alumnos compran dos libros. Dieciséis alumnos compran tres libros. Seis alumnos compran cuatro libros. Cinco estudiantes compran cinco libros. Dos estudiantes compran seis libros.
Debido a que los datos son enteros, resta 0.5 de 1, el valor de datos más pequeño y suma 0.5 a 6, el valor de datos más grande. Entonces el punto de partida es 0.5 y el valor final es 6.5.
A continuación, calcule el ancho de cada barra o intervalo de clase. Si los datos son discretos y no hay demasiados valores diferentes, lo más conveniente es un ancho que coloque los valores de datos en medio del intervalo de barra o clase. Dado que los datos constan de los números 1, 2, 3, 4, 5, 6, y el punto de partida es 0.5, un ancho de uno coloca el 1 en el medio del intervalo de 0.5 a 1.5, el 2 en el medio del intervalo de 1.5 a 2.5, el 3 en el medio del intervalo de 2.5 a 3.5, el 4 en el medio del intervalo de _____ __ a _______, el 5 en el medio del intervalo de _______ a _______, y el _______ en el medio del intervalo de _______ a _______.
Contestar
Calcule el número de barras de la siguiente manera:
\(\frac{6.5 - 0.5}{\text{number of bars}}\) = 1
donde 1 es el ancho de una barra. Por lo tanto, barras = 6.
El siguiente histograma muestra el número de libros en el eje x y la frecuencia en el eje y.

Nota
Ir a [enlace]. Hay instrucciones de calculadora para ingresar datos y para crear un histograma personalizado. Crea el histograma para Ejemplo.
- Presione Y=. Presiona CLEAR para eliminar cualquier ecuación.
- Presione STAT 1:EDIT. Si L1 tiene datos en él, flecha hacia arriba en el nombre L1, presione CLEAR y luego flecha hacia abajo. Si es necesario, haga lo mismo para L2.
- En L1, ingrese 1, 2, 3, 4, 5, 6.
- En L2, ingrese 11, 10, 16, 6, 5, 2.
- Presione VENTANA. Establecer Xmin = .5, Xscl = (6.5 — .5) /6, Ymin = —1, Ymax = 20, Yscl = 1, Xres = 1.
- Presione 2 nd Y=. Comience presionando 4:Plotsoff ENTER.
- Presione 2 nd Y=. Presione 1:Plot1. Presione ENTER. Flecha hacia abajo a TIPO. Flecha a la 3ª imagen (histograma). Presione ENTER.
- Flecha abajo a Xlist: Ingresa L1 (2 nd 1). Flecha hacia abajo a Freq. Ingrese L2 (2 nd 2).
- Presione GRAPH.
- Utilice la tecla TRACE y las teclas de flecha para examinar el histograma.
Ejercicio\(\PageIndex{2}\)
Los siguientes datos son el número de deportes que juegan 50 estudiantes deportistas. El número de deportes es datos discretos ya que se cuentan los deportes.
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1
2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2;
3; 3; 3; 3; 3; 3; 3; 3
20 estudiantes deportistas practican un deporte. 22 estudiantes deportistas practican dos deportes. Ocho estudiantes deportistas practican tres deportes.
Rellene los espacios en blanco para la siguiente oración. Dado que los datos consisten en los números 1, 2, 3, y el punto de partida es 0.5, un ancho de uno coloca el 1 en el medio del intervalo 0.5 a _____, el 2 en el medio del intervalo de _____ a _____, y el 3 en el medio del intervalo de _____ a _____.
Contestar
1.5
1.5 a 2.5
2.5 a 3.5
Ejemplo\(\PageIndex{3}\)
Usando este conjunto de datos, construya un histograma.
| 9.95 | 10 | 2.25 | 16.75 | 0 |
| 19.5 | 22.5 | 7.5 | 15 | 12.75 |
| 5.5 | 11 | 10 | 20.75 | 17.5 |
| 23 | 21.9 | 24 | 23.75 | 18 |
| 20 | 15 | 22.9 | 18.8 | 20.5 |
Contestar

Algunos valores en este conjunto de datos caen en los límites para los intervalos de clase. Un valor se cuenta en un intervalo de clase si cae en el límite izquierdo, pero no si cae en el límite derecho. Diferentes investigadores pueden configurar histogramas para los mismos datos de diferentes maneras. Hay más de una forma correcta de configurar un histograma.
Ejercicio\(\PageIndex{3}\)
Los siguientes datos representan el número de empleados de diversos restaurantes de la ciudad de Nueva York. Usando estos datos, cree un histograma.
22; 35; 15; 26; 40; 28; 18; 20; 25; 34; 39; 42; 24; 22; 19; 27; 22; 34; 40; 20; 38 y 28
Use 10—19 como primer intervalo.
Cuenta el dinero (facturas y cambio) en tu bolsillo o bolso. Su instructor registrará los montos. Como clase, construya un histograma que muestre los datos. Discuta cuántos intervalos cree que es apropiado. Es posible que desee experimentar con el número de intervalos.
Polígonos de frecuencia
Los polígonos de frecuencia son análogos a los gráficos de líneas, y así como los gráficos de líneas hacen que los datos continuos sean visualmente fáciles de interpretar, también lo hacen los polígonos de frecuencia. Para construir un polígono de frecuencia, primero examine los datos y decida el número de intervalos, o intervalos de clase, a utilizar en el eje x y el eje y. Después de elegir los rangos apropiados, comience a trazar los puntos de datos. Después de trazar todos los puntos, dibuja segmentos de línea para conectarlos.
Ejemplo\(\PageIndex{4}\)
Se construyó un polígono de frecuencia a partir de la tabla de frecuencias a continuación.
| Bote Inferior | Encuadernación superior | Frecuencia | Frecuencia Acumulada |
|---|---|---|---|
| 49.5 | 59.5 | 5 | 5 |
| 59.5 | 69.5 | 10 | 15 |
| 69.5 | 79.5 | 30 | 45 |
| 79.5 | 89.5 | 40 | 85 |
| 89.5 | 99.5 | 15 | 100 |

La primera etiqueta en el eje x es 44.5. Esto representa un intervalo que se extiende de 39.5 a 49.5. Dado que el puntaje de prueba más bajo es 54.5, este intervalo se usa solo para permitir que la gráfica toque el eje x. El punto etiquetado 54.5 representa el siguiente intervalo, o el primer intervalo “real” de la tabla, y contiene cinco puntuaciones. Este razonamiento se sigue para cada uno de los intervalos restantes con el punto 104.5 representando el intervalo de 99.5 a 109.5. Nuevamente, este intervalo no contiene datos y solo se usa para que la gráfica toque el eje x. Al mirar la gráfica, decimos que esta distribución está sesgada porque un lado de la gráfica no refleja el otro lado.
Ejercicio\(\PageIndex{4}\)
Construir un polígono de frecuencia de las edades de los presidentes de Estados Unidos en la inauguración que se muestra en la Tabla.
| Edad en la Inauguración | Frecuencia |
|---|---|
| 41.5—46.5 | 4 |
| 46.5—51.5 | 11 |
| 51.5—56.5 | 14 |
| 56.5—61.5 | 9 |
| 61.5—66.5 | 4 |
| 66.5—71.5 | 2 |
Contestar
La primera etiqueta en el eje x es 39. Esto representa un intervalo que se extiende de 36.5 a 41.5. Dado que no hay edades menores a 41.5, este intervalo se usa únicamente para permitir que la gráfica toque el eje x. El punto etiquetado 44 representa el siguiente intervalo, o el primer intervalo “real” de la tabla, y contiene cuatro puntuaciones. Este razonamiento se sigue para cada uno de los intervalos restantes con el punto 74 representando el intervalo de 71.5 a 76.5. Nuevamente, este intervalo no contiene datos y solo se usa para que la gráfica toque el eje x. Al mirar la gráfica, decimos que esta distribución está sesgada porque un lado de la gráfica no refleja el otro lado.
. 
Figura\(\PageIndex{5}\).
Los polígonos de frecuencia son útiles para comparar distribuciones. Esto se logra superponiendo los polígonos de frecuencia dibujados para diferentes conjuntos de datos.
Ejemplo\(\PageIndex{5}\)
Construiremos un polígono de frecuencia de superposición comparando las puntuaciones de Ejemplo con la calificación numérica final de los estudiantes.
| Bote Inferior | Encuadernación superior | Frecuencia | Frecuencia Acumulada |
|---|---|---|---|
| 49.5 | 59.5 | 5 | 5 |
| 59.5 | 69.5 | 10 | 15 |
| 69.5 | 79.5 | 30 | 45 |
| 79.5 | 89.5 | 40 | 85 |
| 89.5 | 99.5 | 15 | 100 |
| Bote Inferior | Encuadernación superior | Frecuencia | Frecuencia Acumulada |
|---|---|---|---|
| 49.5 | 59.5 | 10 | 10 |
| 59.5 | 69.5 | 10 | 20 |
| 69.5 | 79.5 | 30 | 50 |
| 79.5 | 89.5 | 45 | 95 |
| 89.5 | 99.5 | 5 | 100 |

Supongamos que queremos estudiar el rango de temperatura de una región durante todo un mes. Todos los días al mediodía notamos la temperatura y anotamos esto en un registro. Con estos datos se podrían realizar diversos estudios estadísticos. Podríamos encontrar la temperatura media o mediana del mes. Podríamos construir un histograma que muestre el número de días que las temperaturas alcanzan cierto rango de valores. Sin embargo, todos estos métodos ignoran una parte de los datos que hemos recopilado.
Una característica de los datos que tal vez queramos considerar es la del tiempo. Dado que cada fecha está emparejada con la lectura de temperatura del día, no tenemos que pensar en los datos como aleatorios. En cambio, podemos usar los tiempos dados para imponer un orden cronológico a los datos. Un gráfico que reconoce este orden y muestra la temperatura cambiante a medida que avanza el mes se llama gráfico de series de tiempo.
Construyendo un gráfico de series de tiempo
Para construir un gráfico de series de tiempo, debemos mirar ambas piezas de nuestro conjunto de datos emparejados. Comenzamos con un sistema de coordenadas cartesianas estándar. El eje horizontal se utiliza para trazar los incrementos de fecha u hora, y el eje vertical se utiliza para trazar los valores de la variable que estamos midiendo. Al hacer esto, hacemos que cada punto de la gráfica corresponda a una fecha y una cantidad medida. Los puntos en la gráfica suelen estar conectados por líneas rectas en el orden en que ocurren.
Ejemplo\(\PageIndex{6}\)
Los siguientes datos muestran el Índice Anual de Precios al Consumidor, cada mes, por diez años. Construya una gráfica de serie temporal solo para los datos del Índice Anual de Precios al Consumidor.
| Año | Ene | Feb | Mar | Abr | Mayo | Jun | Jul |
|---|---|---|---|---|---|---|---|
| 2003 | 181.7 | 183.1 | 184.2 | 183.8 | 183.5 | 183.7 | 183.9 |
| 2004 | 185.2 | 186.2 | 187.4 | 188.0 | 189.1 | 189.7 | 189.4 |
| 2005 | 190.7 | 191.8 | 193.3 | 194.6 | 194.4 | 194.5 | 195.4 |
| 2006 | 198.3 | 198.7 | 199.8 | 201.5 | 202.5 | 202.9 | 203.5 |
| 2007 | 202.416 | 203.499 | 205.352 | 206.686 | 207.949 | 208.352 | 208.299 |
| 2008 | 211.080 | 211.693 | 213.528 | 214.823 | 216.632 | 218.815 | 219.964 |
| 2009 | 211.143 | 212.193 | 212.709 | 213.240 | 213.856 | 215.693 | 215.351 |
| 2010 | 216.687 | 216.741 | 217.631 | 218.009 | 218.178 | 217.965 | 218.011 |
| 2011 | 220.223 | 221.309 | 223.467 | 224.906 | 225.964 | 225.722 | 225.922 |
| 2012 | 226.665 | 227.663 | 229.392 | 230.085 | 229.815 | 229.478 | 229.104 |
| Año | Ago | Sep | Oct | Nov | Dic | Anual |
|---|---|---|---|---|---|---|
| 2003 | 184.6 | 185.2 | 185.0 | 184.5 | 184.3 | 184.0 |
| 2004 | 189.5 | 189.9 | 190.9 | 191.0 | 190.3 | 188.9 |
| 2005 | 196.4 | 198.8 | 199.2 | 197.6 | 196.8 | 195.3 |
| 2006 | 203.9 | 202.9 | 201.8 | 201.5 | 201.8 | 201.6 |
| 2007 | 207.917 | 208.490 | 208.936 | 210.177 | 210.036 | 207.342 |
| 2008 | 219.086 | 218.783 | 216.573 | 212.425 | 210.228 | 215.303 |
| 2009 | 215.834 | 215.969 | 216.177 | 216.330 | 215.949 | 214.537 |
| 2010 | 218.312 | 218.439 | 218.711 | 218.803 | 219.179 | 218.056 |
| 2011 | 226.545 | 226.889 | 226.421 | 226.230 | 225.672 | 224.939 |
| 2012 | 230.379 | 231.407 | 231.317 | 230.221 | 229.601 | 229.594 |
Contestar

Ejercicio\(\PageIndex{5}\)
La siguiente tabla es una porción de un conjunto de datos de www.worldbank.org. Utilice la tabla para construir una gráfica de series de tiempo para las emisiones de CO 2 para Estados Unidos.
| Ucrania | Reino Unido | Estados Unidos | |
|---|---|---|---|
| 2003 | 352,259 | 540,640 | 5,681,664 |
| 2004 | 343,121 | 540,409 | 5,790,761 |
| 2005 | 339,029 | 541,990 | 5,826,394 |
| 2006 | 327,797 | 542,045 | 5,737,615 |
| 2007 | 328,357 | 528,631 | 5,828,697 |
| 2008 | 323,657 | 522,247 | 5,656,839 |
| 2009 | 272,176 | 474,579 | 5,299,563 |

Usos de un gráfico de series de tiempo
Los gráficos de series temporales son herramientas importantes en diversas aplicaciones de la estadística. Al registrar valores de la misma variable durante un periodo prolongado de tiempo, a veces es difícil discernir alguna tendencia o patrón. Sin embargo, una vez que se muestran gráficamente los mismos puntos de datos, algunas entidades saltan. Los gráficos de series temporales hacen que las tendencias sean fáciles de detectar.
Revisar
Un histograma es una versión gráfica de una distribución de frecuencias. La gráfica consiste en barras de igual ancho dibujadas adyacentes entre sí. La escala horizontal representa clases de valores de datos cuantitativos y la escala vertical representa frecuencias. Las alturas de las barras corresponden a valores de frecuencia. Los histogramas se utilizan típicamente para conjuntos de datos cuantitativos, continuos y grandes. Un polígono de frecuencia también se puede utilizar al graficar grandes conjuntos de datos con puntos de datos que se repiten. Los datos suelen ir en el eje y con la frecuencia graficada en el eje x. Los gráficos de series temporales pueden ser útiles cuando se observan grandes cantidades de datos para una variable durante un período de tiempo.Glosario
Referencias
- Datos sobre homicidios anuales en Detroit, 1961-73, del libro de Gunst & Mason 'Análisis de regresión y su aplicación', Marcel Dekker
- “Cronología: Guía para los presidentes de Estados Unidos: Información sobre el lugar de nacimiento de cada presidente, partido político, mandato y más”. Escolástica, 2013. Disponible en línea en www.scholastic.com/profesores/a... -us-presidentes (consultado el 3 de abril de 2013).
- “Presidentes”. Hecho Monstruo. Pearson Education, 2007. Disponible en línea en http://www.factmonster.com/ipka/A0194030.html (consultado el 3 de abril de 2013).
- “Estadísticas de Seguridad Alimentaria”. Organización de las Naciones Unidas para la Alimentación y la Agricultura. Disponible en línea en http://www.fao.org/economic/ess/ess-fs/en/ (consultado el 3 de abril de 2013).
- “Índice de Precios al Consumidor”. Departamento del Trabajo de Estados Unidos: Buró de Estadísticas Laborales. Disponible en línea en http://data.bls.gov/pdq/SurveyOutputServlet (consultado el 3 de abril de 2013).
- “Emisiones de CO2 (kt).” El Banco Mundial, 2013. Disponible en línea en http://databank.worldbank.org/data/home.aspx (consultado el 3 de abril de 2013).
- “Datos de series de tiempo de nacimientos”. Oficina General de Registro Para Escocia, 2013. Disponible en línea en www.gro-scotland.gov.uk/stati... me-series.html (consultado el 3 de abril de 2013).
- “Demografía: Niños menores de 5 años con bajo peso”. Indexmundi. Disponible en línea en http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (consultado el 3 de abril de 2013).
- Gunst, Richard, Robert Mason. El análisis de regresión y su aplicación: un enfoque orientado a datos. CRC Press: 1980.
- “Sobrepeso y Obesidad: Datos sobre la Obesidad en Centros para el Control y Prevención de Enfermedades. Disponible en línea en http://www.cdc.gov/obesity/data/adult.html (consultado el 13 de septiembre de 2013).
- Frecuencia
- el número de veces que se produce un valor de los datos
- Histograma
- una representación gráfica en\(x-y\) forma de la distribución de datos en un conjunto de datos;\(x\) representa los datos y\(y\) representa la frecuencia, o frecuencia relativa. La gráfica consta de rectángulos contiguos.
- Frecuencia relativa
- la relación entre el número de veces que se produce un valor de los datos en el conjunto de todos los resultados y el número de todos los resultados


