11.7: Prueba de una varianza única
- Page ID
- 153154
Una prueba de una sola varianza supone que la distribución subyacente es normal. Las hipótesis nulas y alternativas se establecen en términos de la varianza poblacional (o desviación estándar poblacional). El estadístico de prueba es:
\[\chi^{2} = \frac{(n-1)s^{2}}{\sigma^{2}} \label{test}\]
donde:
- \(n\)es el número total de datos
- \(s^{2}\)es la varianza de la muestra
- \(\sigma^{2}\)es la varianza poblacional
Se puede pensar en\(s\) como la variable aleatoria en esta prueba. El número de grados de libertad es\(df = n - 1\). Una prueba de una sola varianza puede ser de cola derecha, de cola izquierda o de dos colas. El siguiente ejemplo te mostrará cómo configurar las hipótesis nulas y alternativas. Las hipótesis nulas y alternativas contienen declaraciones sobre la varianza poblacional.
Ejemplo\(\PageIndex{1}\)
Los instructores de matemáticas no solo están interesados en cómo les va a sus alumnos en los exámenes, en promedio, sino en cómo varían los puntajes de los exámenes. Para muchos instructores, la varianza (o desviación estándar) puede ser más importante que el promedio.
Supongamos que un instructor de matemáticas cree que la desviación estándar para su examen final es de cinco puntos. Uno de sus mejores alumnos piensa lo contrario. El alumno afirma que la desviación estándar es de más de cinco puntos. Si el alumno realizara una prueba de hipótesis, ¿cuáles serían las hipótesis nulas y alternativas?
Contestar
A pesar de que se nos da la desviación estándar poblacional, podemos configurar la prueba utilizando la varianza poblacional de la siguiente manera.
- \(H_{0}: \sigma^{2} = 5^{2}\)
- \(H_{a}: \sigma^{2} > 5^{2}\)
Ejercicio\(\PageIndex{1}\)
Un instructor de SCUBA quiere registrar las profundidades colectivas que cada uno de sus alumnos se sumerge durante su checkout. Le interesa cómo varían las profundidades, a pesar de que todos deberían haber estado a la misma profundidad. Cree que la desviación estándar es de tres pies. Su asistente piensa que la desviación estándar es de menos de tres pies. Si el instructor realizara una prueba, ¿cuáles serían las hipótesis nulas y alternativas?
- Contestar
-
- \(H_{0}: \sigma^{2} = 3^{2}\)
- \(H_{a}: \sigma^{2} > 3^{2}\)
Ejemplo\(\PageIndex{2}\)
Con líneas individuales en sus diversas ventanas, una oficina de correos encuentra que la desviación estándar para los tiempos de espera normalmente distribuidos para los clientes el viernes por la tarde es de 7.2 minutos. La oficina de correos experimenta con una sola línea de espera principal y encuentra que para una muestra aleatoria de 25 clientes, los tiempos de espera para los clientes tienen una desviación estándar de 3.5 minutos.
Con un nivel de significancia del 5%, pruebe la afirmación de que una sola línea causa una menor variación entre los tiempos de espera (tiempos de espera más cortos) para los clientes.
Contestar
Dado que la afirmación es que una sola línea causa menos variación, esta es una prueba de una sola varianza. El parámetro es la varianza poblacional\(\sigma^{2}\), o la desviación estándar poblacional,\(\sigma\).
Variable aleatoria: La desviación estándar de la muestra\(s\),, es la variable aleatoria. Vamos\(s = \text{standard deviation for the waiting times}\).
- \(H_{0}: \sigma^{2} = 7.2^{2}\)
- \(H_{a}: \sigma^{2} < 7.2^{2}\)
La palabra “menos” te dice que esta es una prueba de cola izquierda.
Distribución para la prueba:\(\chi^{2}_{24}\), donde:
- \(n = \text{the number of customers sampled}\)
- \(df = n - 1 = 25 - 1 = 24\)
Calcular el estadístico de prueba (Ecuación\ ref {test}):
\[\chi^{2} = \frac{(n-1)s^{2}}{\sigma^{2}} = \frac{(25-1)(3.5)^{2}}{7.2^{2}} = 5.67 \nonumber\]
dónde\(n = 25\),\(s = 3.5\), y\(\sigma = 7.2\).
Gráfica:
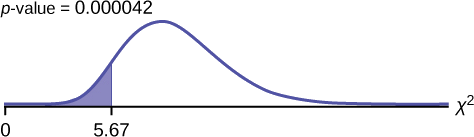
Declaración de probabilidad:\(p\text{-value} = P(\chi^{2} < 5.67) = 0.000042\)
Comparar\(\alpha\) y el\(p\text{-value}\):
\[\alpha = 0.05 (p\text{-value} = 0.000042 \alpha > p\text{-value} \nonumber\]
Tomar una decisión: Desde\(\alpha > p\text{-value}\), rechazar\(H_{0}\). Esto quiere decir que rechazas\(\sigma^{2} = 7.2^{2}\). En otras palabras, no crees que la variación en los tiempos de espera sea de 7.2 minutos; piensas que la variación en los tiempos de espera es menor.
Conclusión: A un nivel de significancia del 5%, a partir de los datos, hay evidencia suficiente para concluir que una sola línea provoca una menor variación entre los tiempos de espera o con una sola línea, los tiempos de espera del cliente varían menos de 7.2 minutos.
En 2do DISTR.T.R., use 7:χ2cdf. La sintaxis es (inferior, superior, df) para la lista de parámetros. Por ejemplo, χ2cdf (-1E99,5.67,24). El\(p\text{-value} = 0.000042\).
Ejercicio\(\PageIndex{2}\)
La FCC realiza pruebas de velocidad de banda ancha para medir la cantidad de datos por segundo que pasan entre la computadora de un consumidor e Internet. A agosto de 2012, la desviación estándar de las velocidades de Internet entre los Proveedores de Servicios de Internet (ISP) era de 12.2 por ciento. Supongamos que se toma una muestra de 15 ISP, y la desviación estándar es 13.2. Un analista afirma que la desviación estándar de velocidades es más de lo que se reportó. Indicar las hipótesis nulas y alternativas, computar los grados de libertad, el estadístico de prueba, esbozar la gráfica del valor p y sacar una conclusión. Prueba al nivel de significancia del 1%.
- Contestar
-
- \(H_{0}: \sigma^{2} = 12.2^{2}\)
- \(H_{a}: \sigma^{2} > 12.2^{2}\)
En
2do DISTR.L, uso7:χ2cdf. La sintaxis es(inferior, superior, df)para la lista de parámetros.χ2cdf (16.39,10^99,14). El\(p\text{-value} = 0.2902\).\(df = 14\)
\[\text{chi}^{2} \text{test statistic} = 16.39 \nonumber\]

Figura\(\PageIndex{2}\). El\(p\text{-value}\) es\(0.2902\), por lo que declinamos rechazar la hipótesis nula. No hay evidencia suficiente para sugerir que la varianza sea mayor que\(12.2^{2}\).
Referencias
- “Guías de precios de AppleInsider”. Apple Insider, 2013. Disponible en línea en http://appleinsider.com/mac_price_guide (consultado el 14 de mayo de 2013).
- Datos del Banco Mundial, 5 de junio de 2012.
Revisar
Para probar la variabilidad, utilice la prueba de chi-cuadrado de una sola varianza. La prueba puede ser izquierda, derecha o de dos colas, y sus hipótesis siempre se expresan en términos de varianza (o desviación estándar).
Revisión de Fórmula
\(\chi^{2} = \frac{(n-1) \cdot s^{2}}{\sigma^{2}}\)Prueba de un único estadístico de varianza donde:
\(n: \text{sample size}\)
\(s: \text{sample standard deviation}\)
\(\sigma: \text{population standard deviation}\)
\(df = n – 1 \text{Degrees of freedom}\)
Prueba de una varianza única
- Utilice la prueba para determinar la variación.
- Los grados de libertad es el\(\text{number of samples} - 1\).
- El estadístico de prueba es\(\frac{(n-1) \cdot s^{2}}{\sigma^{2}}\), dónde\(n = \text{the total number of data}\)\(s^{2} = \text{sample variance}\), y\(\sigma^{2} = \text{population variance}\).
- La prueba puede ser izquierda, derecha o de dos colas.
Usa la siguiente información para responder a los siguientes tres ejercicios: La desviación estándar de un arquero para sus golpes es de seis (los datos se miden en distancia desde el centro del objetivo). Un observador afirma que la desviación estándar es menor.
Ejercicio\(\PageIndex{3}\)
¿Qué tipo de prueba se debe utilizar?
Contestar
una prueba de una sola varianza
Ejercicio\(\PageIndex{4}\)
Indicar las hipótesis nulas y alternativas.
Ejercicio\(\PageIndex{5}\)
¿Es esta una prueba de cola derecha, cola izquierda o de dos colas?
Contestar
una prueba de cola izquierda
Utilice la siguiente información para responder a los siguientes tres ejercicios: La desviación estándar de alturas para los alumnos de una escuela es de 0.81. Se toma una muestra aleatoria de 50 estudiantes, y la desviación estándar de alturas de la muestra es de 0.96. Un investigador a cargo del estudio considera que la desviación estándar de alturas para la escuela es mayor a 0.81.
Ejercicio\(\PageIndex{6}\)
¿Qué tipo de prueba se debe utilizar?
Ejercicio\(\PageIndex{5}\)
Indicar las hipótesis nulas y alternativas.
Contestar
\(H_{0}: \sigma^{2} = 0.81^{2}\);
\(H_{a}: \sigma^{2} > 0.81^{2}\)
Ejercicio\(\PageIndex{6}\)
\(df =\)________
Utilice la siguiente información para responder a los siguientes cuatro ejercicios: El tiempo promedio de espera en el consultorio de un médico varía. La desviación estándar de los tiempos de espera en un consultorio médico es de 3.4 minutos. Una muestra aleatoria de 30 pacientes en el consultorio del médico tiene una desviación estándar de tiempos de espera de 4.1 minutos. Un médico cree que la variación de los tiempos de espera es mayor de lo que se pensaba originalmente.
Ejercicio\(\PageIndex{7}\)
¿Qué tipo de prueba se debe utilizar?
Contestar
una prueba de una sola varianza
Ejercicio\(\PageIndex{8}\)
¿Cuál es el estadístico de prueba?
Ejercicio\(\PageIndex{9}\)
¿Cuál es el\(p\text{-value}\)?
Contestar
0.0542
Ejercicio\(\PageIndex{10}\)
¿Qué se puede concluir en el nivel de significancia del 5%?


