13.2: ANOVA de una vía
- Page ID
- 153470
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
El propósito de una prueba ANOVA unidireccional es determinar la existencia de una diferencia estadísticamente significativa entre varias medias grupales. La prueba en realidad utiliza varianzas para ayudar a determinar si las medias son iguales o no. Para realizar una prueba ANOVA unidireccional, hay varios supuestos básicos a cumplir:
Cinco supuestos básicos de ANOVA unidireccional a cumplir
- Se supone que cada población de la que se toma una muestra es normal.
- Todas las muestras son seleccionadas al azar e independientes.
- Se supone que las poblaciones tienen desviaciones estándar iguales (o varianzas).
- El factor es una variable categórica.
- La respuesta es una variable numérica.
Las hipótesis nulas y alternativas
La hipótesis nula es simplemente que todas las medias poblacionales grupales son iguales. La hipótesis alternativa es que al menos un par de medias es diferente. Por ejemplo, si hay\(k\) grupos:
- \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \dotsc = \mu_{k}\)
- \(H_{a}: \text{At least two of the group means} \mu_{2} = \mu_{3} = \dotsc = \mu_{k} \text{are not equal}\)
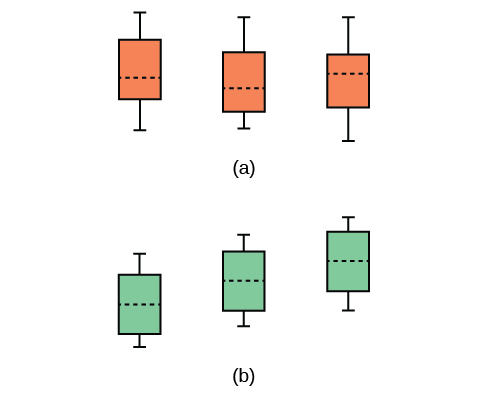
Las gráficas, un conjunto de gráficas de caja que representan la distribución de valores con las medias de grupo indicadas por una línea horizontal a través de la caja, ayudan en la comprensión de la prueba de hipótesis. En la primera gráfica (parcelas de caja roja),\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3}\) y las tres poblaciones tienen la misma distribución si la hipótesis nula es verdadera. La varianza de los datos combinados es aproximadamente la misma que la varianza de cada una de las poblaciones.
Si la hipótesis nula es falsa, entonces la varianza de los datos combinados es mayor que es causada por las diferentes medias como se muestra en la segunda gráfica (gráficas de caja verde).
Revisar
El análisis de varianza extiende la comparación de dos grupos a varios, cada uno un nivel de una variable categórica (factor). Las muestras de cada grupo son independientes y deben seleccionarse aleatoriamente de poblaciones normales con varianzas iguales. Probamos la hipótesis nula de medias iguales de la respuesta en cada grupo versus la hipótesis alternativa de que una o más medias grupales sean diferentes de las otras. Una prueba de hipótesis ANOVA unidireccional determina si varias medias poblacionales son iguales. La distribución para la prueba es la\(F\) distribución con dos grados de libertad diferentes.
Supuestos:
- Se supone que cada población de la que se toma una muestra es normal.
- Todas las muestras son seleccionadas al azar e independientes.
- Se supone que las poblaciones tienen desviaciones estándar iguales (o varianzas).
Glosario
- Análisis de varianza
- también denominado ANOVA, es un método para probar si las medias de tres o más poblaciones son iguales o no. El método es aplicable si:
- todas las poblaciones de interés se distribuyen normalmente.
- las poblaciones tienen desviaciones estándar iguales.
- muestras (no necesariamente del mismo tamaño) se seleccionan al azar e independientemente de cada población.
El estadístico de prueba para el análisis de varianza es el\(F\) -ratio.
- Uno-wayanova
- un método para comprobar si las medias de tres o más poblaciones son iguales o no; el método es aplicable si:
- todas las poblaciones de interés se distribuyen normalmente.
- las poblaciones tienen desviaciones estándar iguales.
- muestras (no necesariamente del mismo tamaño) se seleccionan al azar e independientemente de cada población.
El estadístico de prueba para el análisis de varianza es el\(F\) -ratio.
- Varianza
- media de las desviaciones cuadradas de la media; el cuadrado de la desviación estándar. Para un conjunto de datos, una desviación se puede representar como\(x - \bar{x}\) donde\(x\) es un valor de los datos y\(\bar{x}\) es la media de la muestra. La varianza muestral es igual a la suma de los cuadrados de las desviaciones dividida por la diferencia del tamaño de la muestra y uno.
Colaboradores y Atribuciones
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


