13.4: Datos sobre la distribución F
- Page ID
- 153481
Aquí hay algunos datos sobre la\(F\) distribución:
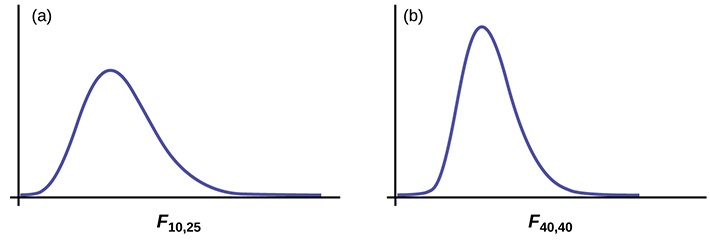
- La curva no es simétrica sino sesgada hacia la derecha.
- Hay una curva diferente para cada conjunto de\(dfs\).
- El\(F\) estadístico es mayor o igual a cero.
- A medida que los grados de libertad para el numerador y para el denominador se hacen más grandes, la curva se aproxima a la normal.
- Otros usos para la\(F\) distribución incluyen comparar dos varianzas y Análisis de varianza bidireccional. El análisis bidireccional está fuera del alcance de este capítulo.
Ejemplo\(\PageIndex{1}\)
Volvamos al ejercicio de rebanar tomate. Las medias de los rendimientos de tomate bajo las cinco condiciones de acolchado están representadas por\(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}, \mu_{5}\). Realizaremos una prueba de hipótesis para determinar si todos los medios son iguales o al menos uno es diferente. Usando un nivel de significancia del 5%, pruebe la hipótesis nula de que no hay diferencia en los rendimientos medios entre los cinco grupos contra la hipótesis alternativa de que al menos una media es diferente del resto.
Responder
Las hipótesis nulas y alternativas son:
- \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5}\)
- \(H_{a}: \mu_{i} \neq \mu_{j}\)algunos\(i \neq j\)
Los resultados de ANOVA de una vía se muestran en la Tabla
| Fuente de variación | Suma de Cuadrados (\(SS\)) | Grados de Libertad (\(df\)) | Cuadrado medio (\(MS\)) | \(F\) |
|---|---|---|---|---|
| Factor (Entre) | \ (SS\))” style="vertical-align:middle; ">36.648,561 | \ (df\))” style="vertical-align:middle; ">\(5 - 1 = 4\) | \ (MS\))” style="vertical-align:middle; ">\(\dfrac{36,648,561}{4} = 9,162,140\) | \ (F\)” style="vertical-align:middle;” class="lt-stats-809">
\(\dfrac{9,162,140}{2,044,672.6} = 4.4810\) |
| Error (Dentro) | \ (SS\))” style="vertical-align:middle; ">20,446,726 | \ (df\))” style="vertical-align:middle; ">\(15 - 5 = 10\) | \ (MS\))” style="vertical-align:middle;” class="lt-stats-809">
\(\dfrac{20,446,726}{10} = 2,044,672.6\) |
\ (F\)” style="vertical-align:middle; "> |
| Total | \ (SS\))” style="vertical-align:middle; ">57.095.287 | \ (df\))” style="vertical-align:middle; ">\(15 - 1 = 14\) | \ (MS\))” style="vertical-align:middle; "> | \ (F\)” style="vertical-align:middle; "> |
Distribución para la prueba:\(F_{4,10}\)
\[df(\text{num}) = 5 - 1 = 4\]
\[df(\text{denom}) = 15 - 5 = 10\]
Estadística de prueba:\(F = 4.4810\)
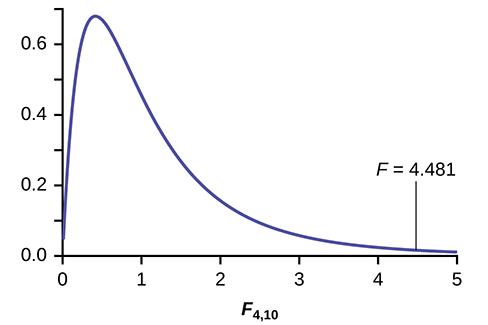
Declaración de probabilidad:\(p\text{-value} = P(F > 4.481) = 0.0248\).
Comparar\(\alpha\) y el\(p\text{-value}\):\(\alpha = 0.05, p\text{-value} = 0.0248\)
Tomar una decisión: Ya que\(\alpha > p\text{-value}\), rechazamos\(H_{0}\).
Conclusión: En el nivel de significancia del 5%, tenemos evidencia razonablemente sólida de que las diferencias en los rendimientos medios para cortar plantas de tomate cultivadas en diferentes condiciones de mulching son improbables debido solo al azar. Podemos concluir que al menos algunos de los mantillo condujeron a diferentes rendimientos medios.
Para encontrar estos resultados en la calculadora:
Presione STAT. Presione 1:EDITAR. Poner los datos en las listas L 1, L 2, L 3, L 4, L 5.
Presione STAT y flecha hacia arriba a PRUEBAS y flecha hacia abajo hasta ANOVA. Pulse ENTER y, a continuación, introduzca L 1, L 2, L 3, L 4, L 5). Presione ENTER. Verá que los valores de la tabla ANOVA anterior son fácilmente producidos por la calculadora, incluyendo el estadístico de prueba y el valor p de la prueba.
La calculadora muestra:
- \(F = 4.4810\)
- \(p = 0.0248\)(\(p\text{-value}\))
Factor
- \(df = 4\)
- \(SS = 36648560.9\)
- \(MS = 9162140.23\)
Error
- \(df = 10\)
- \(SS = 20446726\)
- \(MS = 2044672.6\)
Ejercicio\(\PageIndex{1}\)
El MRSA, o Staphylococcus aureus, puede causar infecciones bacterianas graves en pacientes hospitalarios. El cuadro muestra varios recuentos de colonias de diferentes pacientes que pueden tener o no MRSA.
| Conc = 0.6 | Conc = 0.8 | Conc = 1.0 | Conc = 1.2 | Conc = 1.4 |
|---|---|---|---|---|
| 9 | 16 | 22 | 30 | 27 |
| 66 | 93 | 147 | 199 | 168 |
| 98 | 82 | 120 | 148 | 132 |
Gráfica de los datos para las diferentes concentraciones:

Pruebe si el número medio de colonias es el mismo o diferente. Construye la tabla ANOVA (a mano o usando una calculadora TI-83, 83+ u 84+), encuentra el valor p y expresa tu conclusión. Utilizar un nivel de significancia del 5%.
Responder
Si bien existen diferencias en los diferenciales entre los grupos (Figura\(\PageIndex{1}\)), las diferencias no parecen ser lo suficientemente grandes como para causar preocupación.
Probamos la igualdad del número medio de colonias:
\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5}\)
\(H_{a}: \mu_{i} \neq \mu_{j}\)algunos\(i \neq j\)
Los resultados de la tabla ANOVA unidireccional se muestran en la Tabla.
| Fuente de variación | Suma de Cuadrados (\(SS\)) | Grados de Libertad (\(df\)) | Cuadrado medio (\(MS\)) | \(F\) |
|---|---|---|---|---|
| Factor (Entre) | \ (SS\))” style="vertical-align:middle; ">10.233 | \ (df\))” style="vertical-align:middle; ">\(5 - 1 = 4\) | \ (MS\))” style="vertical-align:middle; ">\(\dfrac{10,233}{4} = 2,558.25\) | \ (F\)” style="vertical-align:middle; ">\(\dfrac{2,558.25}{4,194.9} = 0.6099\) |
| Error (Dentro) | \ (SS\))” style="vertical-align:middle; ">41,949 | \ (df\))” style="vertical-align:middle; ">\(15 - 5 = 10\) | \ (MS\))” style="vertical-align:middle; "> | \ (F\)” style="vertical-align:middle; "> |
| Total | \ (SS\))” style="vertical-align:middle; ">52.182 | \ (df\))” style="vertical-align:middle; ">\(15 - 1 = 14\) | \ (MS\))” style="vertical-align:middle; ">\(\dfrac{41,949}{10} = 4,194.9\) | \ (F\)” style="vertical-align:middle; "> |
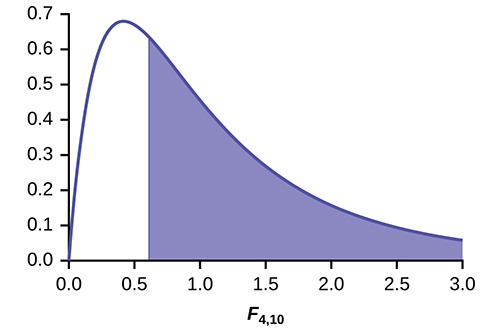
Figura\(\PageIndex{2}\)
Distribución para la prueba:\(F_{4,10}\)
Declaración de probabilidad:\(p\text{-value} = P(F > 0.6099) = 0.6649\).
Comparar\(\alpha\) y el\(p\text{-value}\):\(\alpha = 0.05, p\text{-value} = 0.669, \alpha > p\text{-value}\)
Tomar una decisión: Ya que\(\alpha > p\text{-value}\), no rechazamos\(H_{0}\).
Conclusión: Al nivel de significancia del 5%, no hay evidencia suficiente a partir de estos datos de que diferentes niveles de triptona causarán una diferencia significativa en el número medio de colonias bacterianas formadas.
Ejemplo\(\PageIndex{2}\)
Cuatro hermandades tomaron una muestra aleatoria de hermanas con respecto a sus medias de grado para el último trimestre. Los resultados se muestran en la Tabla.
| Sorority 1 | Sorority 2 | Sorority 3 | Sorority 4 |
|---|---|---|---|
| 2.17 | 2.63 | 2.63 | 3.79 |
| 1.85 | 1.77 | 3.78 | 3.45 |
| 2.83 | 3.25 | 4.00 | 3.08 |
| 1.69 | 1.86 | 2.55 | 2.26 |
| 3.33 | 2.21 | 2.45 | 3.18 |
Usando un nivel de significancia del 1%, ¿existe una diferencia en las calificaciones medias entre las hermandades?
Responder
\(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\)Dejen ser los medios poblacionales de las hermandades. Recuerde que la hipótesis nula afirma que los grupos de hermandad son de la misma distribución normal. La hipótesis alternativa dice que al menos dos de los grupos de hermandad provienen de poblaciones con diferentes distribuciones normales. Observe que los cuatro tamaños de muestra son cinco cada uno.
Este es un ejemplo de un diseño equilibrado, porque cada factor (es decir, hermandad de mujeres) tiene el mismo número de observaciones.
\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4}\)
\(H_{a}\): No todos los medios\(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\) son iguales.
Distribución para la prueba:\(F_{3,16}\)
donde\(k = 4\) grupos y\(n = 20\) muestras en total
\(df(\text{num}) = k - 1 = 4 - 1 = 3\)
\(df(\text{denom}) = n - k = 20 - 4 = 16\)
Calcular el estadístico de prueba:\(F = 2.23\)
Gráfica:
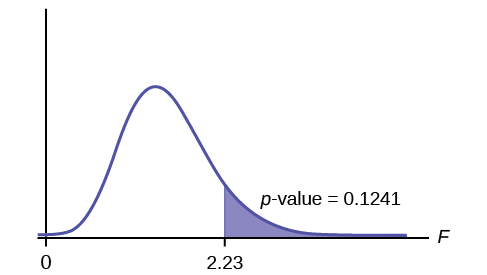
Declaración de probabilidad:\(p\text{-value} = P(F > 2.23) = 0.1241\)
Comparar\(\alpha\) y el\(p\text{-value}\):\(\alpha = 0.01\)
\(p\text{-value} = 0.1241\)
\(\alpha < p\text{-value}\)
Tomar una decisión: Ya que\(\alpha < p\text{-value}\), no se puede rechazar\(H_{0}\).
Conclusión: No hay evidencia suficiente para concluir que existe una diferencia entre las calificaciones medias para las hermandades.
Ponga los datos en listas L 1, L 2, L 3 y L 4. Presiona STAT y flecha hacia PRUEBAS. Flecha hacia abajo a F:ANOVA. Pulse INTRO e Intro (L1, L2, L3, L4).
La calculadora muestra el estadístico F, el\(p\text{-value}\) y los valores para la tabla ANOVA unidireccional:
\(F = 2.2303\)
\(p = 0.1241\)(\(p\text{-value}\))
Factor
\(df = 3\)
\(SS = 2.88732\)
\(MS = 0.96244\)
Error
\(df = 1\)
\(SS = 6.9044\)
\(MS = 0.431525\)
Ejercicio\(\PageIndex{2}\)
Cuatro equipos deportivos tomaron una muestra aleatoria de jugadores con respecto a sus GPA del último año. Los resultados se muestran en la Tabla.
| Basquetbol | Béisbol | Hockey | Lacrosse |
|---|---|---|---|
| 3.6 | 2.1 | 4.0 | 2.0 |
| 2.9 | 2.6 | 2.0 | 3.6 |
| 2.5 | 3.9 | 2.6 | 3.9 |
| 3.3 | 3.1 | 3.2 | 2.7 |
| 3.8 | 3.4 | 3.2 | 2.5 |
Utilizar un nivel de significancia del 5%, y determinar si existe una diferencia en el GPA entre los equipos.
Responder
Con un\(p\text{-value}\) de\(0.9271\), declinamos rechazar la hipótesis nula. No hay pruebas suficientes para concluir que existe una diferencia entre los GPA para los equipos deportivos.
Ejemplo\(\PageIndex{3}\)
Una clase de cuarto grado es estudiar el medio ambiente. Una de las tareas es cultivar plantas de frijol en diferentes suelos. Tommy optó por cultivar sus plantas de frijol en tierra que se encuentra fuera de su aula mezclada con pelusa secadora. Tara eligió cultivar sus plantas de frijol en tierra para macetas comprada en el vivero local. Nick optó por cultivar sus plantas de frijol en tierra del jardín de su madre. No se utilizaron químicos en las plantas, solo agua. Se cultivaron dentro del aula junto a un gran ventanal. Cada niño cultivó cinco plantas. Al final del periodo de crecimiento, se midió cada planta, produciendo los datos (en pulgadas) en la Tabla\(\PageIndex{3}\).
| Plantas de Tommy | Plantas de Tara | Plantas de Nick |
|---|---|---|
| 24 | 25 | 23 |
| 21 | 31 | 27 |
| 23 | 23 | 22 |
| 30 | 20 | 30 |
| 23 | 28 | 20 |
¿Parece que los tres medios en los que se cultivaron las plantas de frijol producen la misma altura media? Prueba a un nivel de significancia del 3%.
Responder
Esta vez, realizaremos los cálculos que conduzcan a la\(F'\) estadística. Observe que cada grupo tiene el mismo número de plantas, por lo que usaremos la fórmula
\[F' = \dfrac{n \cdot s_{\bar{x}}^{2}}{s^{2}_{\text{pooled}}}.\]
Primero, calcular la media muestral y la varianza muestral de cada grupo.
| Plantas de Tommy | Plantas de Tara | Plantas de Nick | |
|---|---|---|---|
| Media de la Muestra | 24.2 | 25.4 | 24.4 |
| Varianza de la muestra | 11.7 | 18.3 | 16.3 |
A continuación, calcular la varianza de las medias de tres grupos (Calcular la varianza de 24.2, 25.4 y 24.4). Varianza de las medias del grupo\(= 0.413 = s_{\bar{x}}^{2}\)
Entonces\(MS_{\text{between}} = ns_{\bar{x}}^{2} = (5)(0.413)\) dónde\(n = 5\) está el tamaño de la muestra (número de plantas que creció cada niño).
Calcular la media de las tres varianzas muestrales (Calcular la media de 11.7, 18.3 y 16.3). Promedio de las varianzas de la muestra\(= 15.433 = s^{2}_{\text{pooled}}\)
Entonces\(MS_{\text{within}} = s^{2}_{\text{pooled}} = 15.433\).
El\(F\) estadístico (o\(F\) ratio) es\(F = \dfrac{MS_{\text{between}}}{MS_{\text{within}}} = \dfrac{ns_{\bar{x}}^{2}}{s^{2}_{\text{pooled}}} = \dfrac{(5)(0.413)}{15.433} = 0.134\)
El\(dfs\) para el numerador\(= \text{the number of groups} - 1 = 3 - 1 = 2\).
El\(dfs\) para el denominador\(= \text{the total number of samples} - \text{the number of groups} = 15 - 3 = 12\)
La distribución para la prueba es\(F_{2,12}\) y el\(F\) estadístico es\(F = 0.134\)
El\(p\text{-value}\) es\(P(F > 0.134) = 0.8759\).
Decisión: Desde\(\alpha = 0.03\) y el\(p\text{-value} = 0.8759\), no rechace\(H_{0}\). (¿Por qué?)
Conclusión: Con un nivel de significancia de 3%, a partir de los datos de la muestra, la evidencia no es suficiente para concluir que las alturas medias de las plantas de frijol son diferentes.
Para calcular el\(p\text{-value}\):
*Prensa 2ª DISTR.C/
*Flecha hacia abajo hasta Fcdf (y presiona ENTER.
*Entrar 0.134, E99, 2, 12)
*Presione ENTER
El\(p\text{-value}\) es\(0.8759\).
Ejercicio\(\PageIndex{3}\)
Otro estudiante de cuarto grado también cultivó plantas de frijol, pero esta vez en una masa gelatinosa. Las alturas fueron (en pulgadas) 24, 28, 25, 30 y 32. Hacer una prueba ANOVA unidireccional en los cuatro grupos. ¿Las alturas de las plantas de frijol son diferentes? Utilice el mismo método que se muestra en Ejemplo\(\PageIndex{3}\).
Responder
- \(F = 0.9496\)
- \(p\text{-value} = 0.4402\)
A partir de los datos de la muestra, la evidencia no es suficiente para concluir que las alturas medias de las plantas de frijol son diferentes.
Ejercicio Colaborativo
De la clase, crear cuatro grupos del mismo tamaño de la siguiente manera: hombres menores de 22 años, hombres al menos 22, mujeres menores de 22 años, mujeres al menos 22. Haga que cada miembro de cada grupo registre el número de estados en los Estados Unidos que haya visitado. Ejecutar una prueba ANOVA para determinar si el número promedio de estados visitados en los cuatro grupos es el mismo. Prueba a un nivel de significancia del 1%. Utilice una de las hojas de solución en [link].
Referencias
- Datos de un aula de cuarto grado en 1994 en una escuela privada K — 12 en San José, CA.
- Mano, D.J., F. Daly, A.D. Lunn, K.J. McConway y E. Ostrowski. Manual de pequeños conjuntos de datos: datos para la fecundidad de la mosca frutífera. Londres: Chapman & Hall, 1994.
- Mano, D.J., F. Daly, A.D. Lunn, K.J. McConway y E. Ostrowski. Un manual de pequeños conjuntos de datos. Londres: Chapman & Hall, 1994, pg. 50.
- Mano, D.J., F. Daly, A.D. Lunn, K.J. McConway y E. Ostrowski. Un manual de pequeños conjuntos de datos. Londres: Chapman & Hall, 1994, pg. 118.
- “Clasificaciones MLB — 2012.” Disponible en línea en http://espn.go.com/mlb/standings/_/year/2012.
- Mackowiak, P. A., Wasserman, S. S., y Levine, M. M. (1992), “Una evaluación crítica de 98.6 grados F, el límite superior de la temperatura corporal normal, y otros legados de Carl Reinhold August Wunderlich”, Revista de la Asociación Médica Americana, 268, 1578-1580.
Revisar
La gráfica de la\(F\) distribución es siempre positiva y sesgada a la derecha, aunque la forma puede ser montada o exponencial dependiendo de la combinación de numerador y denominador grados de libertad. El\(F\) estadístico es la relación de una medida de la variación en las medias del grupo a una medida similar de la variación dentro de los grupos. Si la hipótesis nula es correcta, entonces el numerador debe ser pequeño comparado con el denominador. Se producirá una pequeña\(F\) estadística, y el área bajo la\(F\) curva a la derecha será grande, representando una grande\(p\text{-value}\). Cuando la hipótesis nula de medias de grupo iguales es incorrecta, entonces el numerador debe ser grande comparado con el denominador, dando una\(F\) estadística grande y un área pequeña (pequeña\(p\text{-value}\)) a la derecha del estadístico bajo la\(F\) curva.
Cuando los datos tienen tamaños de grupo desiguales (datos desequilibrados), entonces las técnicas discutidas anteriormente deben usarse para cálculos manuales. Sin embargo, en el caso de los datos balanceados (los grupos son del mismo tamaño), se pueden utilizar cálculos simplificados basados en medias y varianzas de grupo. En la práctica, por supuesto, el software suele emplearse en el análisis. Como en cualquier análisis, se deben utilizar gráficas de diversos tipos en conjunto con técnicas numéricas. ¡Siempre mira tus datos!


