5.3: Cálculos de probabilidad para variables aleatorias normales generales
- Page ID
- 151162
Objetivos de aprendizaje
- Aprender a calcular probabilidades relacionadas con cualquier variable aleatoria normal.
Si\(X\) es alguna variable aleatoria normal normalmente distribuida entonces Figura también se\(\PageIndex{1}\) puede utilizar para calcular una probabilidad de la forma
igualdad
Si\(X\) es una variable aleatoria normalmente distribuida con media\(\mu\) y desviación estándar\(\sigma\), entonces\[P(a<X<b)=P\left ( \frac{a-\mu }{\sigma }<Z<\frac{b-\mu }{\sigma } \right )\] donde\(Z\) denota una variable aleatoria normal estándar. \(a\)puede ser cualquier número decimal o\(-\infty\);\(b\) puede ser cualquier número decimal o\(\infty\).


Los nuevos puntos finales
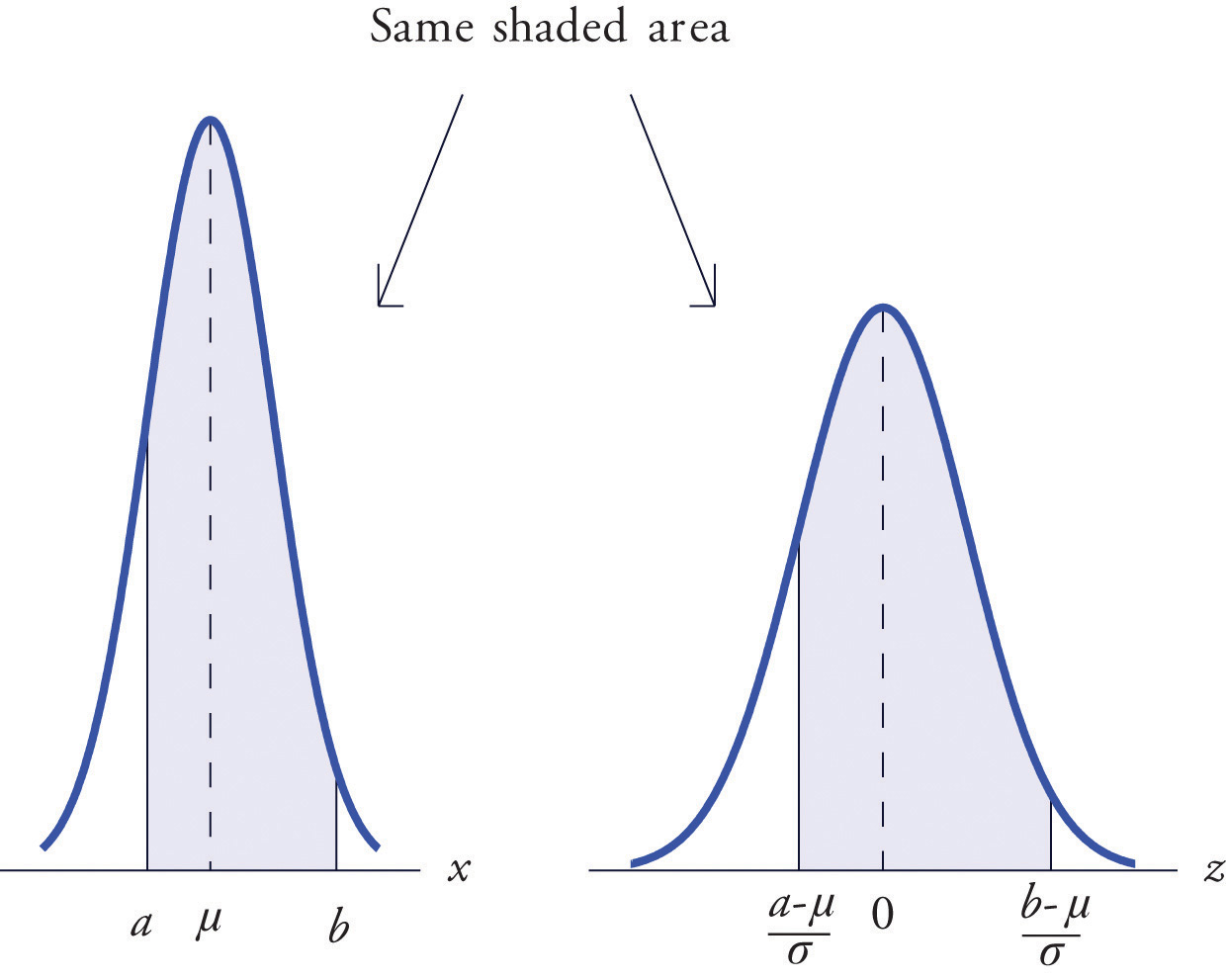
La figura\(\PageIndex{2}\) ilustra el significado de la igualdad geométricamente: las dos regiones sombreadas, una bajo la curva de densidad para\(X\) y la otra debajo de la curva de densidad para\(Z\), tienen la misma área. Sin embargo, en lugar de dibujar ambas curvas de campana, siempre dibujaremos una sola curva genérica en forma de campana con un\(x\) eje -eje y un\(z\) eje debajo de él.
Ejemplo\(\PageIndex{1}\)
Dejar\(X\) ser una variable aleatoria normal con media\(\mu =10\) y desviación estándar\(\sigma =2.5\). Calcula las siguientes probabilidades.
- \(P(X<14)\).
- \(P(8<X<14)\).
Solución:
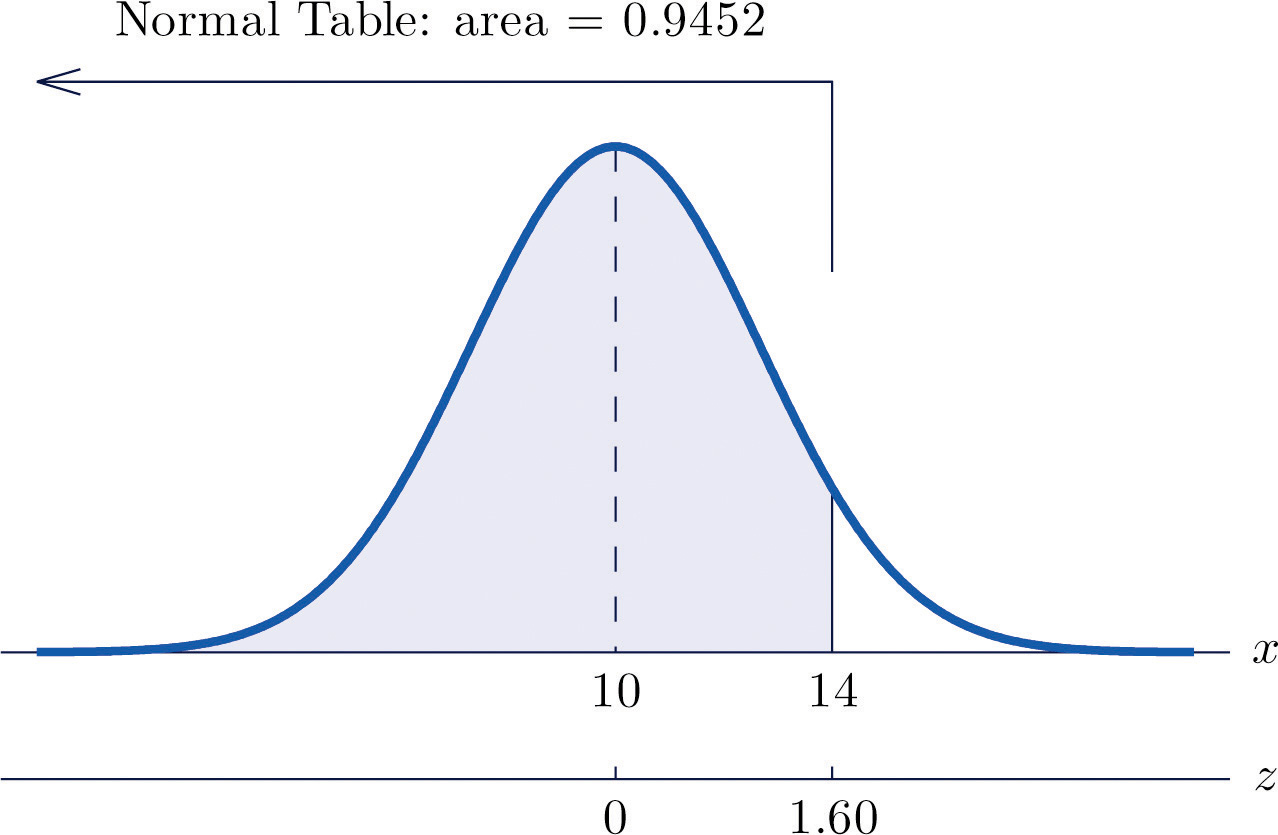
- Ver Figura\(\PageIndex{3}\) “Cálculos de Probabilidad para una Variable Aleatoria Normal General”. \[\begin{align*} P(X<14) &= P\left ( Z<\frac{14-\mu }{\sigma } \right )\\ &= P\left ( Z<\frac{14-10}{2.5} \right )\\ &= P(Z<1.60)\\ &= 0.9452 \end{align*}\]
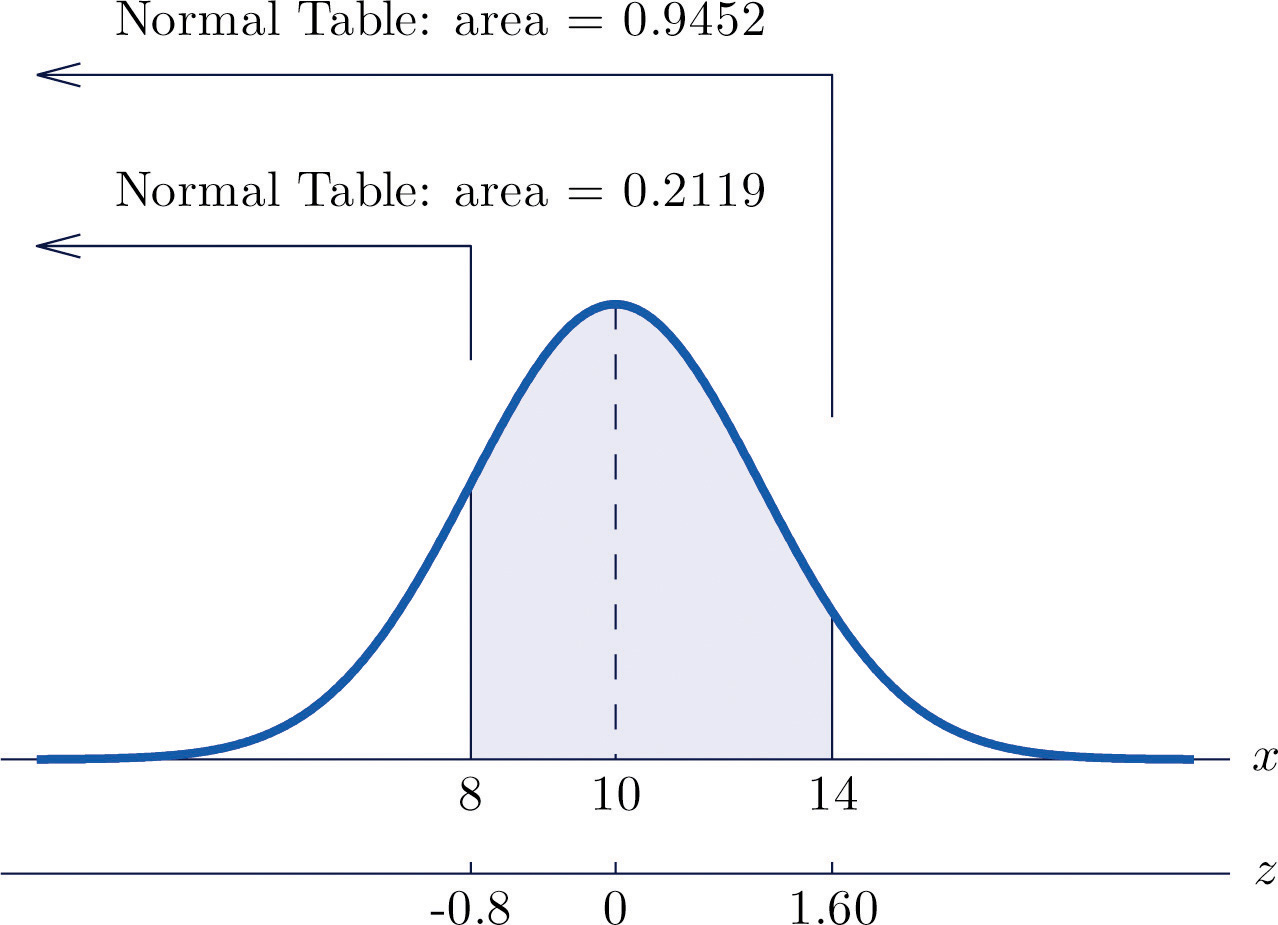
- Ver Figura\(\PageIndex{4}\) “Cálculos de Probabilidad para una Variable Aleatoria Normal General”. \[\begin{align*} P(8<X<14) &= P\left ( \frac{8-10}{2.5}<Z<\frac{14-10}{2.5} \right )\\ &= P\left ( -0.80<Z<1.60 \right )\\ &= 0.9452-0.2119\\ &= 0.7333 \end{align*}\]
Ejemplo\(\PageIndex{2}\)
Las vidas de la banda de rodadura de un determinado neumático de automóvil se distribuyen normalmente con\(37,500\) millas medias y millas de desviación\(4,500\) estándar. Encuentre la probabilidad de que la vida útil de la banda de rodadura de una llanta seleccionada al azar esté entre\(30,000\) y\(40,000\) millas.
Solución:
Dejar\(X\) denotar la vida de la banda de rodadura de un neumático seleccionado al azar. Para facilitar el trabajo con los números elegiremos miles de millas como unidades. Así\(\mu =37.5,\; \sigma =4.5\), y el problema es computar
\[\begin{align*} P(30<X<40) &= P\left ( \frac{30-\mu }{\sigma }<Z<\frac{40-\mu }{\sigma } \right )\\ &= P\left ( \frac{30-37.5}{4.5}<Z<\frac{40-37.5}{4.5} \right )\\ &= P\left ( -1.67<Z<0.56\right )\\ &= 0.7123-0.0475\\ &= 0.6648 \end{align*}\]
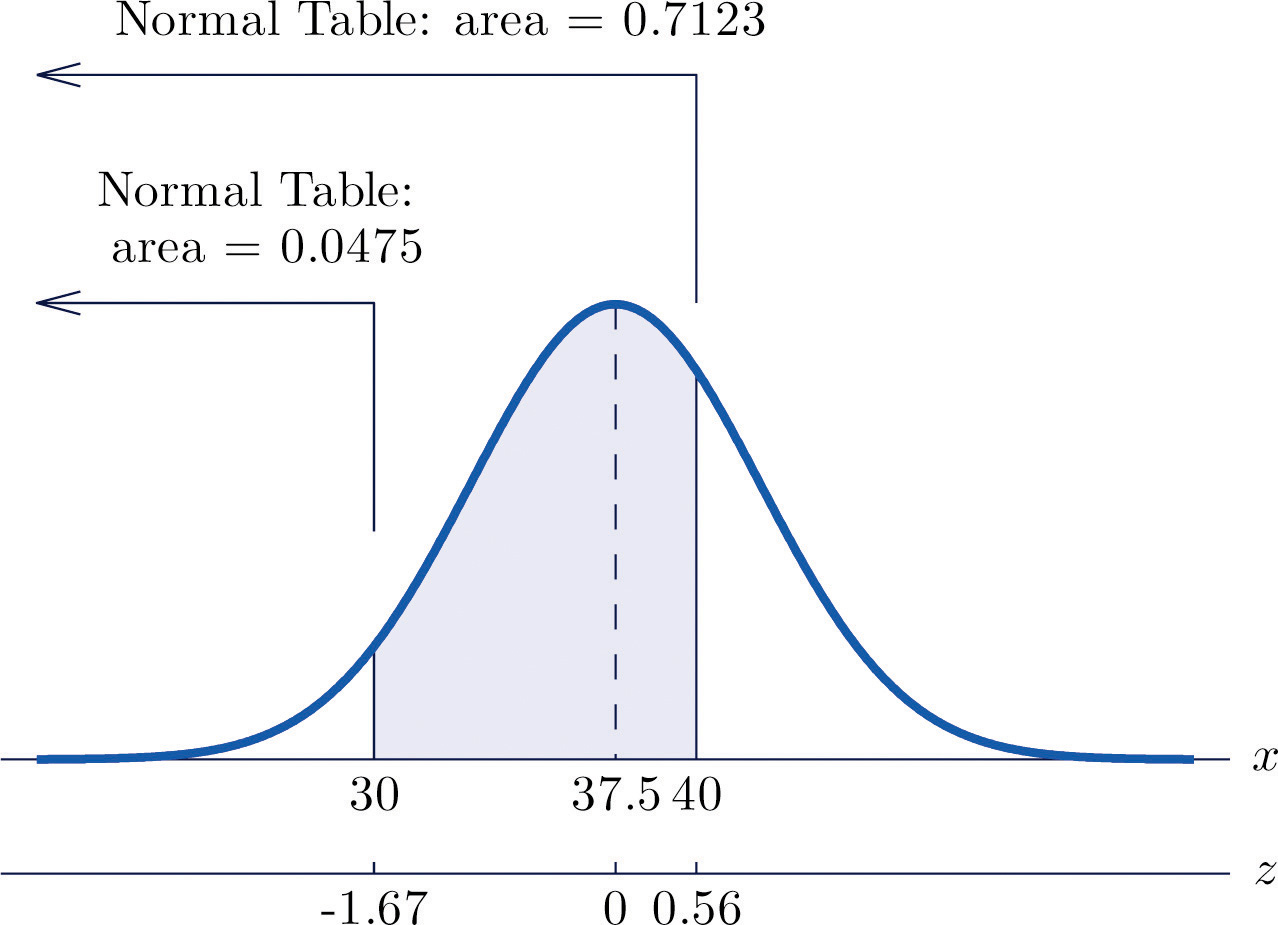
Obsérvese que las dos\(z\) puntuaciones se redondearon a dos decimales para utilizar la Figura\(\PageIndex{1}\) “Probabilidad Normal Acumulada”.
Ejemplo\(\PageIndex{3}\)
Los puntajes en un examen estandarizado de ingreso a la universidad (CEE) se distribuyen normalmente con media\(510\) y desviación estándar\(60\). Una universidad selectiva considera para la admisión solo a los aspirantes con puntajes superiores a CEE\(650\). Encontrar porcentaje de todas las personas que tomaron el CEE que cumplen con el requisito CEE de la universidad para su consideración para la admisión.
Solución:
Dejar\(X\) denotar la puntuación realizada en el CEE por un individuo seleccionado al azar. Entonces\(X\) se distribuye normalmente con media\(510\) y desviación estándar\(60\). La probabilidad de que se\(X\) encuentre en un intervalo determinado es la misma que la proporción de todas las puntuaciones de los exámenes que se encuentran en ese intervalo. Así la solución al problema es\(P(X>650)\), expresada como porcentaje. La figura\(\PageIndex{6}\) “Cálculos de probabilidad para las puntuaciones de los exámenes” ilustra el siguiente cálculo:
\[\begin{align*} P(X>650) &= P\left ( Z>\frac{650-\mu }{\sigma } \right )\\ &= P\left ( Z>\frac{650-510}{60} \right )\\ &= P(Z>2.33)\\ &= 1-0.9901\\ &= 0.0099 \end{align*}\]
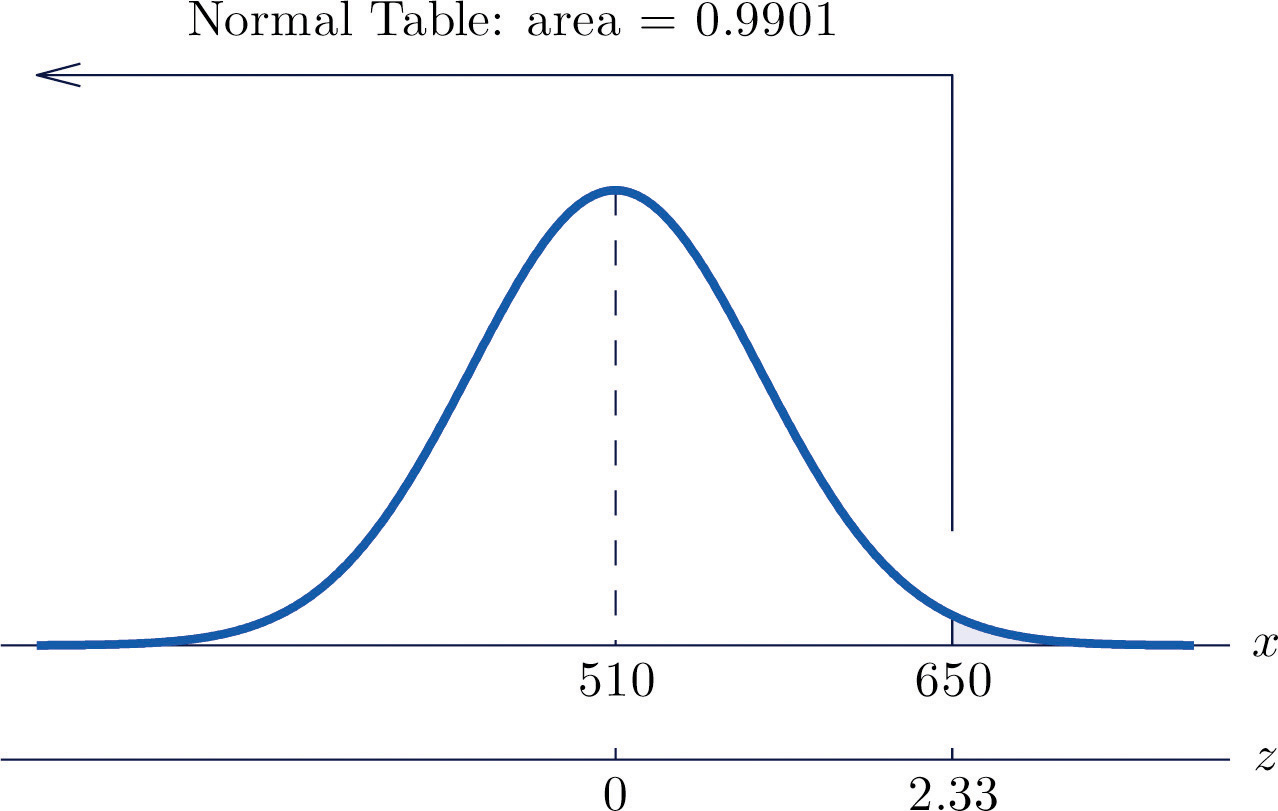
La proporción de todos los puntajes de CEE que superan\(650\) es\(0.0099\), por lo tanto\(0.99\%\) o sobre\(1\%\) hacer.
llave para llevar
- Las probabilidades para una variable aleatoria normal general se calculan usando Figura\(\PageIndex{1}\) después de convertir\(x\) -valores a\(z\) -scores.

