5.4: Áreas de Colas de Distribuciones
- Page ID
- 151158
Objetivos de aprendizaje
- Aprender a encontrar, para una variable aleatoria normal\(X\) y un área\(a\), el valor\(x^\ast\) de\(X\) así que\(P(X<x^\ast )=a\) o aquello\(P(X>x^\ast )=a\), lo que se requiera.
Definición: Colas Izquierda y Derecha
La cola izquierda de una curva\(y=f(x)\) de densidad de una variable aleatoria continua\(X\) cortada por un valor\(x^\ast\) de\(X\) es la región bajo la curva que está a la izquierda de\(x^\ast\), como lo muestra el sombreado en la Figura\(\PageIndex{1}\) (a). La cola derecha cortada por\(x^\ast\) se define de manera similar, como lo indica el sombreado en la Figura\(\PageIndex{1}\) (b).
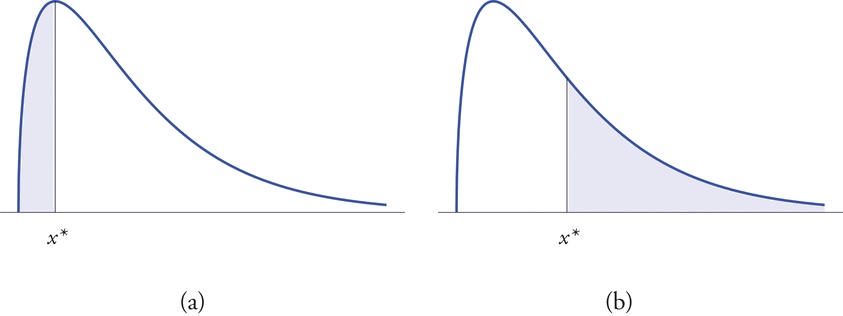
Las probabilidades tabuladas en la Figura 5.3.1 son áreas de colas izquierdas en la distribución normal estándar.
Colas de la Distribución Normal Estándar
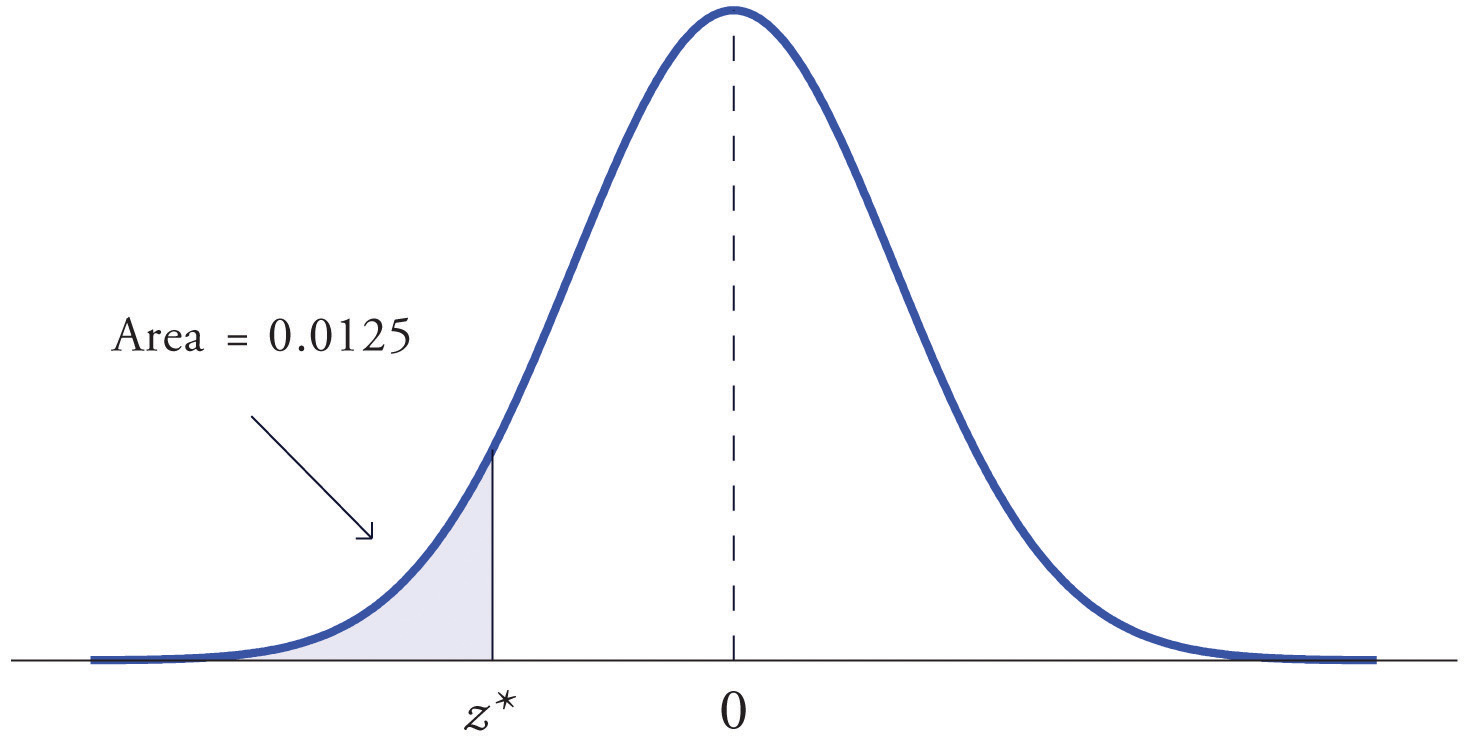
En ocasiones es importante poder resolver el tipo de problema ilustrado por la Figura\(\PageIndex{2}\). Tenemos en mente una cierta área específica, en este caso la zona\(0.0125\) de la región sombreada en la figura, y queremos encontrar el valor\(z^\ast\) de\(Z\) que la produce. Esto es exactamente lo contrario del tipo de problemas encontrados hasta el momento. En lugar de conocer un valor\(z^\ast\) de\(Z\) y encontrar un área correspondiente, conocemos la zona y queremos encontrar\(z^\ast\). En el caso que nos ocupa, en la terminología de la definición justo arriba, deseamos encontrar el valor\(z^\ast\) que corta una cola izquierda de área\(0.0125\) en la distribución normal estándar.
La idea de resolver tal problema es bastante simple, aunque a veces su implementación puede ser un poco complicada. En pocas palabras, se lee la tabla de probabilidad acumulativa para\(Z\) a la inversa, buscando el área relevante en el interior de la tabla y leyendo el valor de\(Z\) desde los márgenes.
Ejemplo\(\PageIndex{1}\)
Encuentra el valor\(z^\ast\) de\(Z\) según lo determinado por la Figura\(\PageIndex{2}\): el valor\(z^\ast\) que corta una cola izquierda del área\(0.0125\) en la distribución normal estándar. En símbolos, encuentra el número\(z^\ast\) tal que\(P(Z<z^\ast )=0.0125\).
Solución:
El número que se conoce,\(0.0125\), es el área de una cola izquierda, y como ya se mencionó las probabilidades tabuladas en la Figura 5.3.1 son áreas de colas izquierdas. Así, para resolver este problema sólo necesitamos buscar en el interior de la Figura 5.3.1 el número\(0.0125\). Se encuentra en la fila con el encabezado\(-2.2\) y en la columna con el encabezado\(0.04\). Esto significa que\(P(Z < -2.24)= 0.0125\), de ahí\(z^\ast=-2.24\).
Ejemplo\(\PageIndex{2}\)
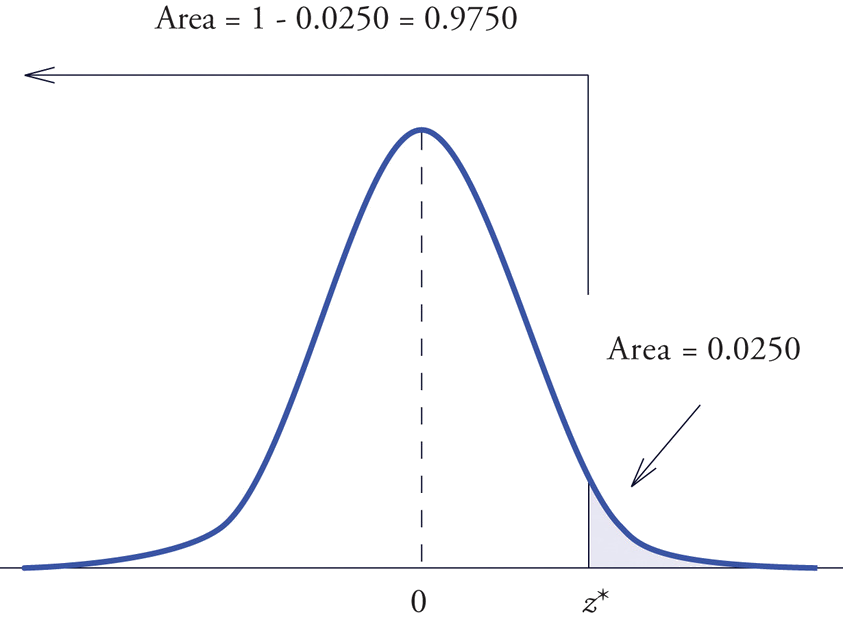
Encuentra el valor\(z^\ast\) de\(Z\) según lo determinado por la Figura\(\PageIndex{3}\): el valor\(z^\ast\) que corta una cola derecha de área\(0.0250\) en la distribución normal estándar. En símbolos, encuentra el número\(z^\ast\) tal que\(P(Z >z^\ast)= 0.0250\).
Solución:
La distinción importante entre este ejemplo y el anterior es que aquí es el área de una cola derecha la que se conoce. Para poder utilizar la Figura 5.3.1 primero debemos encontrar esa zona de la cola izquierda cortada por el número desconocido\(z^\ast\). Dado que el área total bajo la curva de densidad es\(1\), esa área es\(1-0.0250=0.9750\). Este es el número que buscamos en el interior de la Figura 5.3.1. Se encuentra en la fila con el encabezado\(1.9\) y en la columna con el encabezado\(0.06\). Por lo tanto\(z^\ast=1.96\).
Definición: variable aleatoria normal estándar
Se denota el valor de la variable aleatoria normal estándar\(Z\) que corta una cola derecha del área\(c\)\(z_c\). Por simetría, el valor de\(Z\) que corta una cola izquierda del área\(c\) es\(-z_c\). Ver Figura\(\PageIndex{4}\).
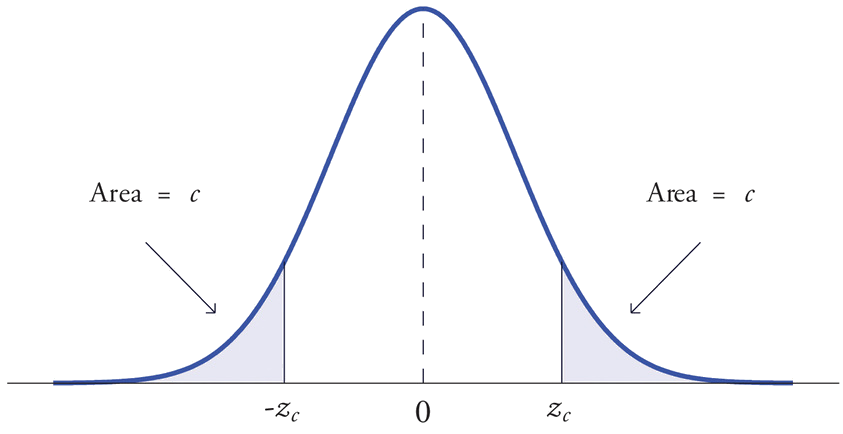
Los dos ejemplos anteriores fueron atípicos porque las áreas que buscábamos en el interior de la Figura 5.3.1 estaban realmente ahí. El siguiente ejemplo ilustra la situación que es más común.
Ejemplo\(\PageIndex{3}\)
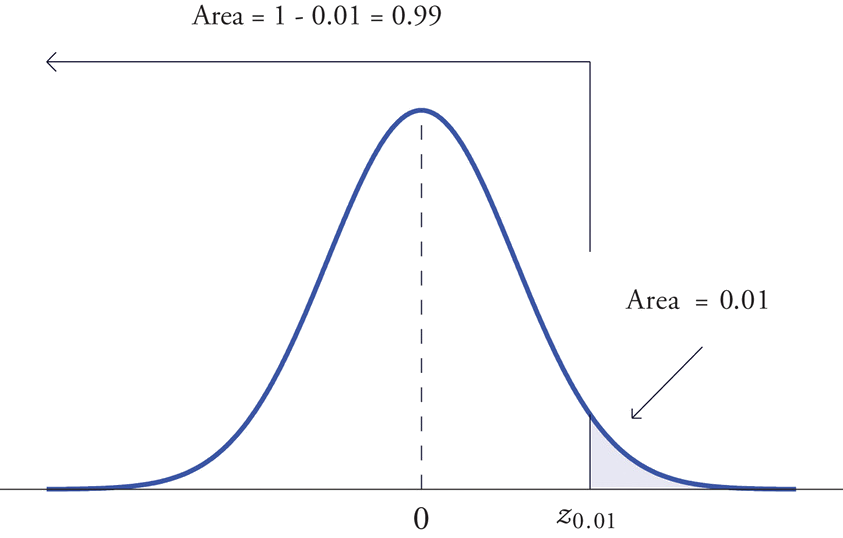
Encuentra\(z_{.01}\) y\(-z_{.01}\), los valores de\(Z\) ese corte las colas derecha e izquierda del área\(0.01\) en la distribución normal estándar.
Solución:
Ya que\(-z_{.01}\) corta una cola izquierda de área\(0.01\) y la Figura 5.3.1 es una tabla de colas izquierdas, buscamos el número\(0.0100\) en el interior de la mesa. No está ahí, sino que cae entre los dos números\(0.0102\) y\(0.0099\) en la fila con rumbo\(-2.3\). El número\(0.0099\) está\(0.0100\) más cerca de lo que\(0.0102\) es, así que para las centésimas lugar en\(-z_{.01}\) usamos el encabezado de la columna que contiene\(0.0099\), es decir,\(0.03\), y escribir\(-z_{.01}\approx -2.33\).
La respuesta a la segunda mitad del problema es automática: ya que\(-z_{.01}=-2.33\), concluimos inmediatamente que\(z_{.01}=2.33\).
Bien podríamos haber resuelto este problema buscando\(z_{.01}\) primero, y es instructivo volver a trabajar el problema de esta manera. Para empezar, primero debemos restar\(0.01\) de\(1\) para encontrar el área\(1-0.0100=0.9900\) de la cola izquierda cortada por el número desconocido\(z_{.01}\). Ver Figura\(\PageIndex{5}\). Después buscamos el área\(0.9900\) en Figura\(\PageIndex{5}\). No está ahí, sino que cae entre los números\(0.9898\) y\(0.9901\) en la fila con rumbo\(2.3\). Ya que\(0.9901\) está\(0.9900\) más cerca de lo que\(0.9898\) es, utilizamos el encabezamiento de columna por encima de ella\(0.03\),, para obtener la aproximación\(z_{.01}\approx 2.33\). Entonces finalmente\(-z_{.01}\approx -2.33\).
Colas de distribuciones normales generales
También surge el problema\(x^\ast\) de encontrar el valor de una variable aleatoria general normalmente distribuida\(X\) que corta una cola de un área especificada. Este problema puede resolverse en dos pasos.
- Supongamos que\(X\) es una variable aleatoria normalmente distribuida con media\(\mu\) y desviación estándar\(\sigma\). Para encontrar el valor\(x^\ast\) de\(X\) que corta una cola izquierda o derecha de área\(c\) en la distribución de\(X\):
- encontrar el valor\(z^\ast\) de\(Z\) que corta una cola izquierda o derecha del área\(c\) en la distribución normal estándar;\(z^\ast\) es la\(z\) -score de\(x^\ast\); computar\(x^\ast\) usando la fórmula de desandardización\[x^\ast =\mu +z^\ast \sigma\]
En definitiva, resolver el problema correspondiente para la distribución normal estándar, obteniendo con ello la\(z\) -score de\(x^\ast\), luego desandardizar para obtener\(x^\ast\).
Ejemplo\(\PageIndex{4}\)
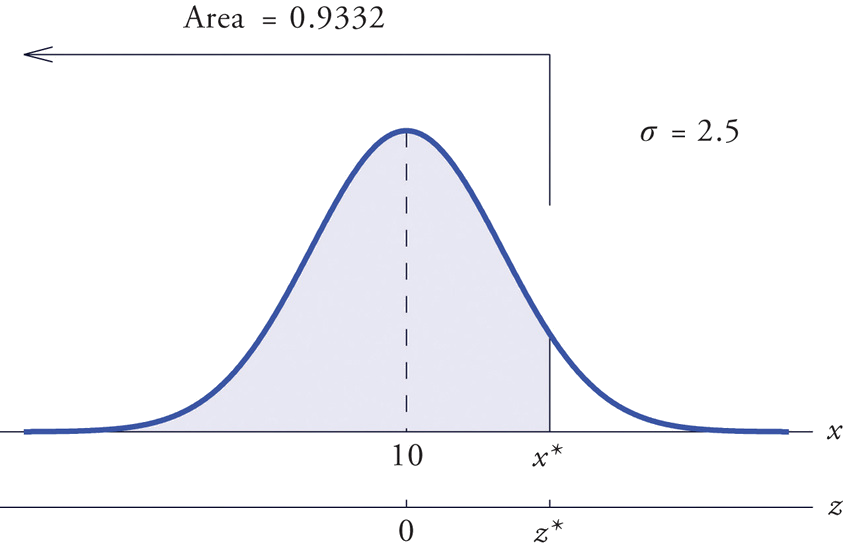
Encuentra\(x^\ast\) tal que\(P(X<x^\ast )=0.9332\), donde\(X\) es una variable aleatoria normal con media\(\mu =10\) y desviación estándar\(\sigma =2.5\).
Solución:
Todas las ideas para la solución se ilustran en la Figura\(\PageIndex{6}\). Dado que\(0.9332\) es el área de una cola izquierda, podemos encontrar\(z^\ast\) simplemente buscando\(0.9332\) en el interior de la Figura 5.3.1. Está en la fila y columna con encabezamientos\(1.5\) y\(0.00\), de ahí\(z^\ast=1.50\). Por\(x^\ast\) lo tanto, las desviaciones\(1.50\) estándar por encima de la media,
\[x^\ast =\mu +z^\ast \sigma =10+(1.50)\cdot (0.2)=13.75\]
Ejemplo\(\PageIndex{5}\)
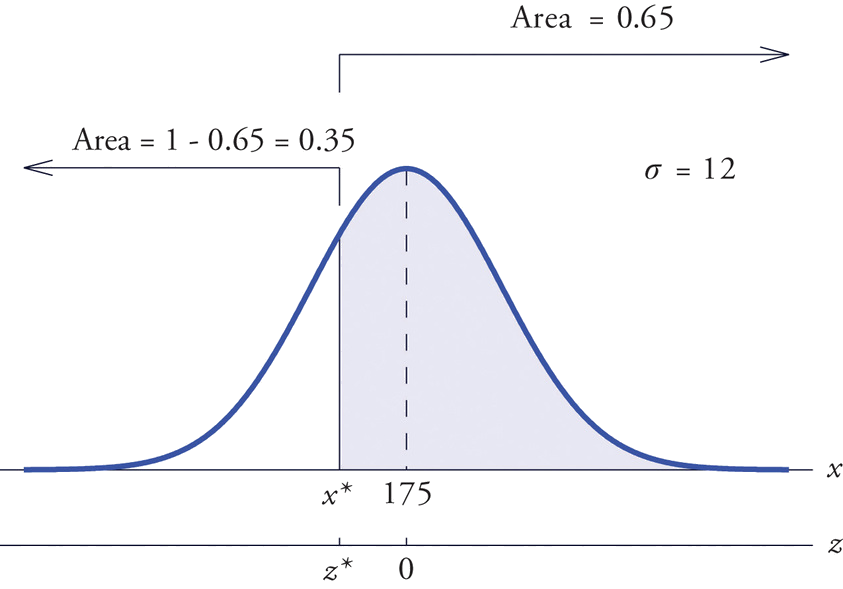
Encuentra\(x^\ast\) tal que\(P(X>x^\ast )=0.65\), donde\(X\) es una variable aleatoria normal con media\(\mu =175\) y desviación estándar\(\sigma =12\).
Solución:
La situación se ilustra en la Figura\(\PageIndex{7}\). Dado que\(0.65\) es el área de una cola derecha, primero la restamos\(1\) para obtener\(1-0.65=0.35\), el área de la cola izquierda complementaria. Nos encontramos\(z^\ast\) buscando\(0.3500\) en el interior de la Figura 5.3.1. No está presente, sino que se encuentra entre las entradas de la tabla\(0.3520\) y\(0.3483\). La entrada\(0.3483\) con encabezamientos de fila\(-0.3\) y columna y\(0.09\) está\(0.3500\) más cerca que la otra entrada, entonces\(z^\ast \approx -0.39\). Por\(x^\ast\) lo tanto, las desviaciones\(0.39\) estándar por debajo de la media,
\[x^\ast =\mu +z^\ast \sigma =175+(-0.39)\cdot (12)=170.32\]
Ejemplo\(\PageIndex{6}\)
Los puntajes en un examen estandarizado de ingreso a la universidad (CEE) se distribuyen normalmente con media\(510\) y desviación estándar\(60\). Una universidad selectiva decide dar seria consideración para la admisión a los aspirantes cuyos puntajes de CEE están en la parte superior\(5\%\) de todas las puntuaciones de CEE. Encuentra la puntuación mínima que cumpla con este criterio para consideración seria para la admisión.
Solución:
Dejar\(X\) denotar la puntuación realizada en el CEE por un individuo seleccionado al azar. Entonces\(X\) se distribuye normalmente con media\(510\) y desviación estándar\(60\). La probabilidad de que se\(X\) encuentre en un intervalo determinado es la misma que la proporción de todas las puntuaciones de los exámenes que se encuentran en ese intervalo. Así, la puntuación mínima que está en la parte superior\(5\%\) de todos los CEE es la puntuación\(x^\ast\) que corta una cola derecha en la distribución\(X\) del área\(0.05\) (\(5\%\)expresada como una proporción). Ver Figura\(\PageIndex{8}\).
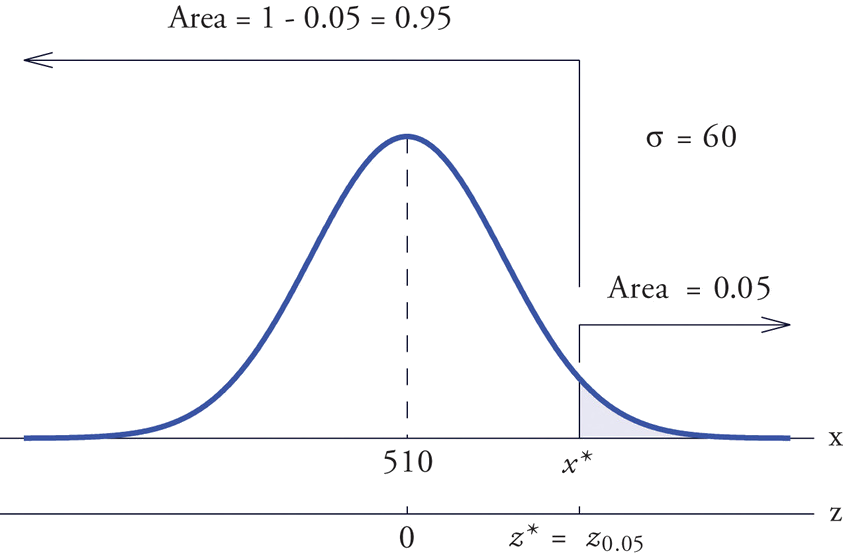
Dado que\(0.0500\) es el área de una cola derecha, primero la restamos\(1\) para obtener\(1-0.0500=0.9500\), el área de la cola izquierda complementaria. Nos encontramos\(z^\ast =z_{.05}\) buscando\(0.9500\) en el interior de la Figura 5.3.1. No está presente, y se encuentra exactamente a medio camino entre las dos entradas más cercanas que están,\(0.9495\) y\(0.9505\). En el caso de un empate como este, siempre promediaremos los valores de\(Z\) correspondientes a las dos entradas de tabla, obteniendo aquí el valor\(z^\ast =1.645\). Usando este valor, concluimos que\(x^\ast\) es desviaciones\(1.645\) estándar por encima de la media, por lo que
\[x^\ast =\mu +z^\ast \sigma =510+(1.645)\cdot (60)=608.7\]
Ejemplo\(\PageIndex{7}\)
Todos los niños de una escuela militar deben cursar un curso fijo lo más rápido posible como parte de un examen físico. Los tiempos de acabado se distribuyen normalmente con\(29\) minutos medios y minutos de desviación\(2\) estándar. La mitad\(75\%\) de todos los tiempos de finalización se clasifican como “promedio”. Encuentra el rango de tiempos que son tiempos promedio de finalización por esta definición.
Solución:
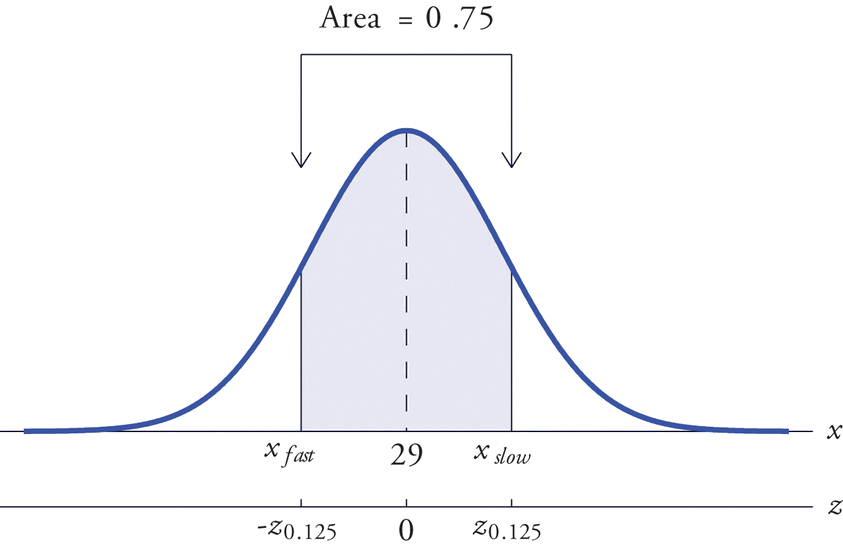
Dejar\(X\) denotar el tiempo de finalización de un niño seleccionado al azar. Entonces\(X\) se distribuye normalmente con media\(29\) y desviación estándar\(2\). La probabilidad de que se\(X\) encuentre en un intervalo determinado es la misma que la proporción de todos los tiempos de finalización que se encuentran en ese intervalo. Así la situación es como se muestra en la Figura\(\PageIndex{9}\). Debido a que el área en el medio correspondiente a los tiempos “promedio” es\(0.75\), las áreas de las dos colas suman\(1 - 0.75 = 0.25\) en total. Por la simetría de la curva de densidad cada cola debe tener la mitad de este total, o área\(0.125\) cada una. Así el tiempo más rápido que es “promedio” tiene\(z\) -score\(-z_{.125}\), que por la Figura 5.3.1 es\(-1.15\), y el tiempo más lento que es “promedio” tiene\(z\) -score\(z_{.125}=1.15\). Los tiempos más rápidos y lentos que aún se consideran promedio son
\[x_{fast}=\mu +(-z_{.125})\sigma =29+(-1.15)\cdot (2)=26.7\]
y
\[x_{slow}=\mu +z_{.125}\sigma =29+(1.15)\cdot (2)=31.3\]
Un niño tiene un tiempo promedio de finalización si corre el curso con un tiempo entre\(26.7\) y\(31.3\) minutos, o equivalentemente entre\(26\) minutos\(42\) segundos y\(31\) minutos\(18\) segundos.
Claves para llevar
- El problema de encontrar el número\(z^\ast\) para que la probabilidad\(P(Z<z^\ast )\) sea un valor especificado\(c\) se resuelve buscando el número\(c\) en el interior de la Figura 5.3.1 y leyendo\(z^\ast\) desde los márgenes.
- El problema de encontrar el número\(z^\ast\) para que la probabilidad\(P(Z>z^\ast )\) sea un valor especificado\(c\) se resuelve buscando la probabilidad complementaria\(1-c\) en el interior de la Figura 5.3.1 y leyendo\(z^\ast\) desde los márgenes.
- Para una variable aleatoria normal\(X\) con media\(\mu\) y desviación estándar\(\sigma\), el problema de encontrar el número\(x^\ast\) para que\(P(X<x^\ast )\) sea un valor especificado\(c\) (o así que\(P(X>x^\ast )\) sea un valor especificado\(c\)) se resuelve en dos pasos:
- (1) resolver el problema correspondiente para\(Z\) con el mismo valor de\(c\), obteniendo con ello el\(z\) -score,\(z^\ast\), de\(x^\ast\);
- (2) encontrar\(x^\ast\) usando\(x^\ast =\mu +z^\ast \sigma\).
- Se denota el valor de\(Z\) que corta una cola derecha de área\(c\) en la distribución normal estándar\(z_c\).

