10.4: La línea de regresión de mínimos cuadrados
- Page ID
- 151168
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Aprender a medir qué tan bien se ajusta una línea recta a una colección de datos.
- Aprender a construir la línea de regresión de mínimos cuadrados, la línea recta que mejor se ajusta a una colección de datos.
- Aprender el significado de la pendiente de la línea de regresión de mínimos cuadrados.
- Aprender a usar la línea de regresión de mínimos cuadrados para estimar la variable de respuesta\(y\) en términos de la variable predictora\(x\).
Bondad de Ajuste de una Línea Recta a Datos
Una vez dibujado el diagrama de dispersión de los datos y los supuestos del modelo descritos en las secciones anteriores al menos verificados visualmente (y quizás el coeficiente de correlación\(r\) calculado para verificar cuantitativamente la tendencia lineal), el siguiente paso en el análisis es encontrar la línea recta que mejor se ajusta a los datos. Explicaremos cómo medir qué tan bien se ajusta una línea recta a una colección de puntos examinando qué tan bien\(y=\frac{1}{2}x-1\) se ajusta la línea al conjunto de datos
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array}\]
(que se utilizará como ejemplo de ejecución para las siguientes tres secciones). Escribiremos la ecuación de esta línea como\(\hat{y}=\frac{1}{2}x-1\) con un acento en el\(y\) para indicar que los\(y\) -valores calculados usando esta ecuación no son de los datos. Esto lo haremos con todas las líneas aproximando conjuntos de datos. La línea\(\hat{y}=\frac{1}{2}x-1\) fue seleccionada como una que parece ajustarse razonablemente bien a los datos.
La idea de medir la bondad de ajuste de una línea recta a los datos se ilustra en la Figura\(\PageIndex{1}\), en la que la gráfica de la línea se\(\hat{y}=\frac{1}{2}x-1\) ha superpuesto sobre la gráfica de dispersión para el conjunto de datos de muestra.
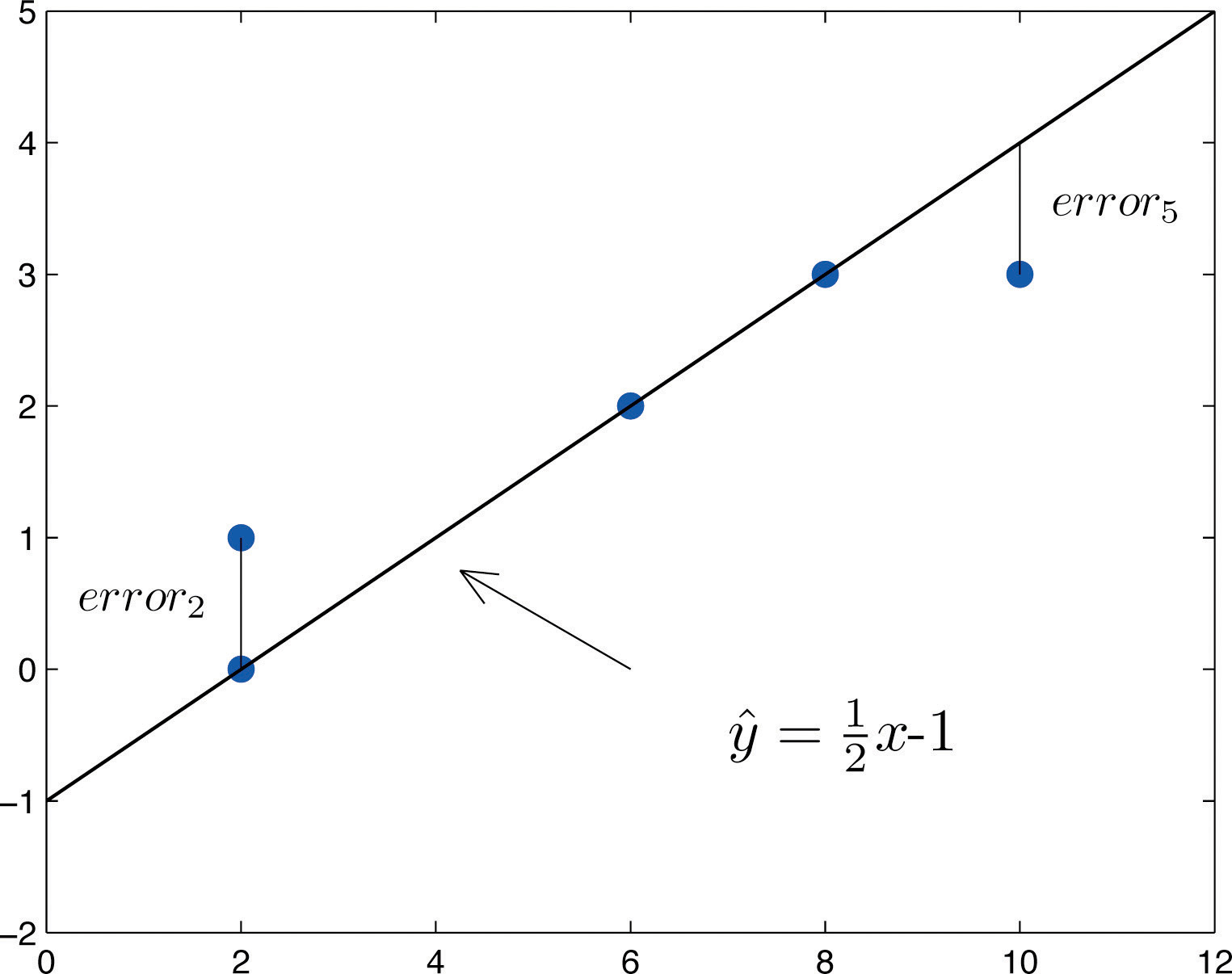
A cada punto del conjunto de datos se le asocia un “error”, la distancia vertical positiva o negativa del punto a la línea: positivo si el punto está por encima de la línea y negativo si está por debajo de la línea. El error se puede calcular como el\(y\) valor real del punto menos el\(y\) -valor\(\hat{y}\) que se “predice” insertando el\(x\) -valor del punto de datos en la fórmula para la línea:
\[\text{error at data point(x,y)}=(\text{true y})−(\text{predicted y})=y−\hat{y}\]
El cálculo del error para cada uno de los cinco puntos del conjunto de datos se muestra en la Tabla\(\PageIndex{1}\).
| \(x\) | \(y\) | \(\hat{y}=\frac{1}{2}x-1\) | \(y-\hat{y}\) | \((y-\hat{y})^2\) | |
|---|---|---|---|---|---|
| \ (x\) ">2 | \ (y\) ">0 | \ (\ hat {y} =\ frac {1} {2} x-1\) ">0 | \ (y-\ hat {y}\) ">0 | \ ((y-\ hat {y}) ^2\) ">0 | |
| \ (x\) ">2 | \ (y\) ">1 | \ (\ hat {y} =\ frac {1} {2} x-1\) ">0 | \ (y-\ hat {y}\) ">1 | \ ((y-\ hat {y}) ^2\) ">1 | |
| \ (x\) ">6 | \ (y\) ">2 | \ (\ hat {y} =\ frac {1} {2} x-1\) ">2 | \ (y-\ hat {y}\) ">0 | \ ((y-\ hat {y}) ^2\) ">0 | |
| \ (x\) ">8 | \ (y\) ">3 | \ (\ hat {y} =\ frac {1} {2} x-1\) ">3 | \ (y-\ hat {y}\) ">0 | \ ((y-\ hat {y}) ^2\) ">0 | |
| \ (x\) ">10 | \ (y\) ">3 | \ (\ hat {y} =\ frac {1} {2} x-1\) ">4 | \ (y-\ hat {y}\) ">−1 | \ ((y-\ hat {y}) ^2\) ">1 | |
| \(\sum\) | \ (x\) ">- | \ (y\) ">- | \ (\ hat {y} =\ frac {1} {2} x-1\) ">- | \ (y-\ hat {y}\) ">0 | \ ((y-\ hat {y}) ^2\) ">2 |
Un primer pensamiento para una medida de la bondad de ajuste de la línea a los datos sería simplemente agregar los errores en cada punto, pero el ejemplo muestra que esto no puede funcionar bien en general. La línea no se ajusta perfectamente a los datos (ninguna línea puede), sin embargo, debido a la cancelación de errores positivos y negativos la suma de los errores (la cuarta columna de números) es cero. En cambio, la bondad de ajuste se mide por la suma de los cuadrados de los errores. La cuadratura elimina los signos menos, por lo que no puede ocurrir ninguna cancelación. Para los datos y la línea en\(\PageIndex{1}\) la Figura la suma de los errores al cuadrado (la última columna de números) es\(2\). Este número mide la bondad de ajuste de la línea a los datos.
Definición: bondad de ajuste
La bondad de ajuste de una línea\(\hat{y}=mx+b\) a un conjunto de\(n\) pares\((x,y)\) de números en una muestra es la suma de los errores al cuadrado
\[\sum (y−\hat{y})^2\]
(\(n\)términos en la suma, uno por cada par de datos).
La línea de regresión de mínimos cuadrados
Dada cualquier colección de pares de números (excepto cuando todos los\(x\) valores -son iguales) y el diagrama de dispersión correspondiente, siempre existe exactamente una línea recta que se ajusta mejor a los datos que cualquier otra, en el sentido de minimizar la suma de los errores al cuadrado. Se llama la línea de regresión de mínimos cuadrados. Además hay fórmulas para su pendiente e\(y\) -intercepción.
Definición: Línea de regresión de mínimos cuadrados
Dada una colección de pares\((x,y)\) de números (en la que no todos los\(x\) valores -son iguales), existe una línea\(\hat{y}=\hat{β}_1x+\hat{β}_0\) que mejor se ajusta a los datos en el sentido de minimizar la suma de los errores al cuadrado. Se llama la línea de regresión de mínimos cuadrados. Su pendiente\(\hat{β}_1\) e\(y\) intercepción\(\hat{β}_0\) se calculan usando las fórmulas
\[\hat{β}_1=\dfrac{SS_{xy}}{SS_{xx}}\]
y
\[\hat{β}_0=\overline{y} - \hat{β}_1 x\]
donde
\[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2\]
y
\[ SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right )\]
\(\bar{x}\)es la media de todos los\(x\) -valores,\(\bar{y}\) es la media de todos los\(y\) -valores, y\(n\) es el número de pares en el conjunto de datos.
La ecuación
\[\hat{y}=\hat{β}_1x+\hat{β}_0\]
especificar la línea de regresión de mínimos cuadrados se llama la ecuación de regresión de mínimos cuadrados.
Recuerde de la Sección 10.3 que la línea con la ecuación\(y=\beta _1x+\beta _0\) se llama la línea de regresión poblacional. Los números\(\hat{\beta _1}\) y\(\hat{\beta _0}\) son estadísticas que estiman los parámetros poblacionales\(\beta _1\) y\(\beta _0\).
Calcularemos la línea de regresión de mínimos cuadrados para el conjunto de datos de cinco puntos, luego para un ejemplo más práctico que será otro ejemplo corriente para la introducción de nuevos conceptos en esta y las siguientes tres secciones.
Ejemplo\(\PageIndex{2}\)
Buscar la línea de regresión de mínimos cuadrados para el conjunto de datos de cinco puntos
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array}\]
y verificar que se ajuste mejor a los datos que la línea\(\hat{y}=\frac{1}{2}x-1\) considerada en la Sección 10.4.1 anterior.
Solución:
En la práctica real, el cálculo de la línea de regresión se realiza utilizando un paquete de cómputos estadísticos. Para aclarar el significado de las fórmulas mostramos los cómputos en forma tabular.
| \(x\) | \(y\) | \(x^2\) | \(xy\) | |
|---|---|---|---|---|
| \ (x\) ">2 | \ (y\) ">0 | \ (x^2\) ">4 | \ (xy\) ">0 | |
| \ (x\) ">2 | \ (y\) ">1 | \ (x^2\) ">4 | \ (xy\) ">2 | |
| \ (x\) ">6 | \ (y\) ">2 | \ (x^2\) ">36 | \ (xy\) ">12 | |
| \ (x\) ">8 | \ (y\) ">3 | \ (x^2\) ">64 | \ (xy\) ">24 | |
| \ (x\) ">10 | \ (y\) ">3 | \ (x^2\) ">100 | \ (xy\) ">30 | |
| \(\sum\) | \ (x\) ">28 | \ (y\) ">9 | \ (x^2\) ">208 | \ (xy\) ">68 |
En la última línea de la tabla tenemos la suma de los números en cada columna. Utilizándolos calculamos:
\[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2=208-\frac{1}{5}(28)^2=51.2\]
\[SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right )=68-\frac{1}{5}(28)(9)=17.6\]
\[\bar{x}=\frac{\sum x}{n}=\frac{28}{5}=5.6\\ \bar{y}=\frac{\sum y}{n}=\frac{9}{5}=1.8\]
para que
\[\hat{β}_1=\dfrac{SS_{xy}}{SS_{xx}}=\dfrac{17.6}{51.2}=0.34375\]
y
\[\hat{β}_0=\bar{y}−\hat{β}_1x−=1.8−(0.34375)(5.6)=−0.125\]
La línea de regresión de mínimos cuadrados para estos datos es
\[\hat{y}=0.34375 x−0.125\]
Los cálculos para medir qué tan bien se ajusta a los datos de la muestra se dan en la Tabla\(\PageIndex{2}\). La suma de los errores al cuadrado es la suma de los números en la última columna, que es\(0.75\). Es menor que\(2\), la suma de los errores al cuadrado para el ajuste de la línea\(\hat{y}=\frac{1}{2}x-1\) a este conjunto de datos.
| \(x\) | \(y\) | \(\hat{y}=0.34375x-0.125\) | \(y-\hat{y}\) | \((y-\hat{y})^2\) |
|---|---|---|---|---|
| \ (x\) ">2 | \ (y\) ">0 | \ (\ hat {y} =0.34375x-0.125\) ">0.5625 | \ (y-\ hat {y}\) ">−0.5625 | \ ((y-\ hat {y}) ^2\) ">0.31640625 |
| \ (x\) ">2 | \ (y\) ">1 | \ (\ hat {y} =0.34375x-0.125\) ">0.5625 | \ (y-\ hat {y}\) ">0.4375 | \ ((y-\ hat {y}) ^2\) ">0.19140625 |
| \ (x\) ">6 | \ (y\) ">2 | \ (\ hat {y} =0.34375x-0.125\) ">1.9375 | \ (y-\ hat {y}\) ">0.0625 | \ ((y-\ hat {y}) ^2\) ">0.00390625 |
| \ (x\) ">8 | \ (y\) ">3 | \ (\ hat {y} =0.34375x-0.125\) ">2.6250 | \ (y-\ hat {y}\) ">0.3750 | \ ((y-\ hat {y}) ^2\) ">0.14062500 |
| \ (x\) ">10 | \ (y\) ">3 | \ (\ hat {y} =0.34375x-0.125\) ">3.3125 | \ (y-\ hat {y}\) ">−0.3125 | \ ((y-\ hat {y}) ^2\) ">0.09765625 |
Ejemplo\(\PageIndex{3}\)
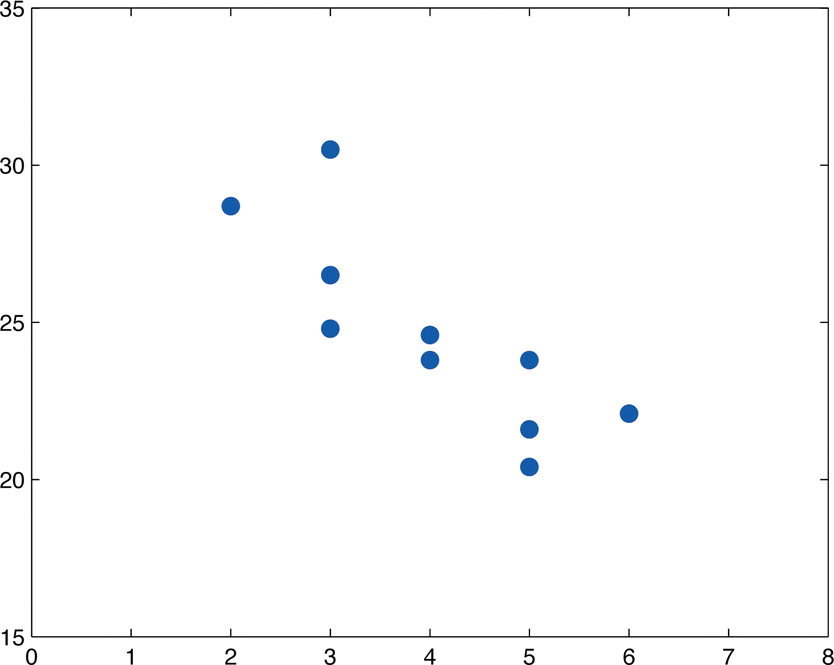
El cuadro\(\PageIndex{3}\) muestra la edad en años y el valor de venta en miles de dólares de una muestra aleatoria de diez automóviles de la misma marca y modelo.
- Construye el diagrama de dispersión.
- Calcular el coeficiente de correlación lineal\(r\). Interpretar su valor en el contexto del problema.
- Calcular la línea de regresión de mínimos cuadrados. Trócalo en el diagrama de dispersión.
- Interpretar el significado de la pendiente de la línea de regresión de mínimos cuadrados en el contexto del problema.
- Supongamos que se selecciona al azar un automóvil de cuatro años de esta marca y modelo. Utilice la ecuación de regresión para predecir su valor minorista.
- Supongamos que se selecciona al azar\(20\) un automóvil de un año de esta marca y modelo. Utilice la ecuación de regresión para predecir su valor minorista. Interpretar el resultado.
- Comente sobre la validez del uso de la ecuación de regresión para predecir el precio de un automóvil nuevo de esta marca y modelo.
| \(x\) | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \ (x\) ">\(y\) | 28.7 | 24.8 | 26.0 | 30.5 | 23.8 | 24.6 | 23.8 | 20.4 | 21.6 | 22.1 |
Solución:
- El diagrama de dispersión se muestra en la Figura\(\PageIndex{2}\).
-
Primero debemos computar\(SS_{xx},\; SS_{xy},\; SS_{yy}\), lo que significa computación\(\sum x,\; \sum y,\; \sum x^2,\; \sum y^2\; \text{and}\; \sum xy\). Utilizando un dispositivo informático obtenemos\[\sum x=40\; \; \sum y=246.3\; \; \sum x^2=174\; \; \sum y^2=6154.15\; \; \sum xy=956.5\]\[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2=174-\frac{1}{10}(40)^2=14\\ SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right )=956.5-\frac{1}{10}(40)(246.3)=-28.7\\ SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=6154.15-\frac{1}{10}(246.3)^2=87.781\] Así que\[r=\frac{SS_{xy}}{\sqrt{SS_{xx}\cdot SS_{yy}}}=\frac{-28.7}{\sqrt{(14)(87.781)}}=-0.819\] la edad y el valor de esta marca y modelo de automóvil están moderadamente fuertemente correlacionados negativamente. A medida que aumenta la edad, el valor del automóvil tiende a disminuir.
-
Usando los valores de\(\sum x\) y\(\sum y\) calculados en la parte (b),\[\bar{x}=\frac{\sum x}{n}=\frac{40}{10}=4\\ \bar{y}=\frac{\sum y}{n}=\frac{246.3}{10}=24.63\] Por lo tanto, usando los valores de\(SS_{xx}\) y\(SS_{xy}\) de la parte (b),\[\hat{\beta _1}=\frac{SS_{xy}}{SS_{xx}}=\frac{-28.7}{14}=-2.05\] y\[\hat{\beta _0}=\bar{y}-\hat{\beta _1}x=24.63-(-2.05)(4)=32.83\] La ecuación\(\bar{y}=\hat{\beta _1}x+\hat{\beta _0}\) de la línea de regresión de mínimos cuadrados para estos datos de muestra es\[\hat{y}=−2.05x+32.83\]
La figura\(\PageIndex{3}\) muestra el diagrama de dispersión con la gráfica de la línea de regresión de mínimos cuadrados superpuesta.
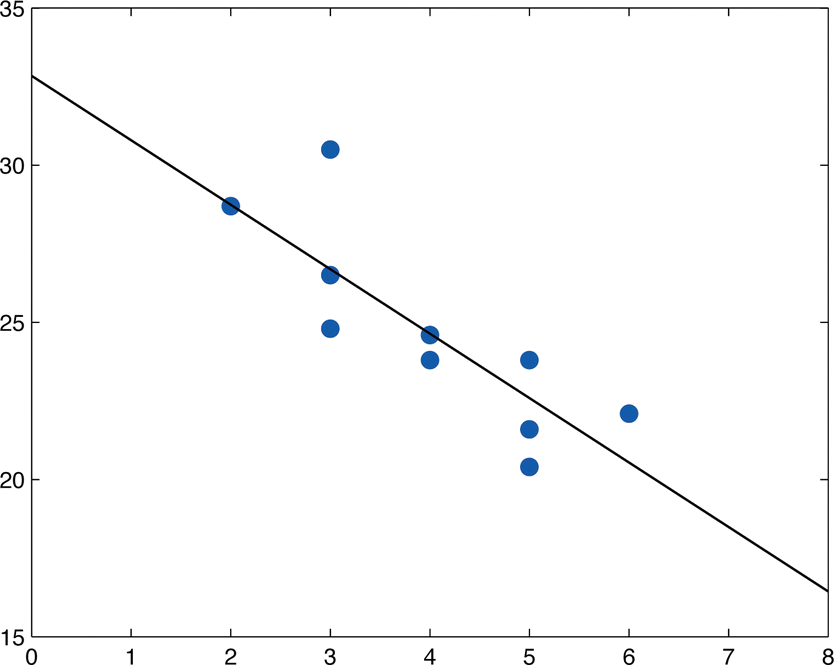
- La pendiente\(-2.05\) significa que por cada unidad se incrementa en\(x\) (año adicional de edad) el valor promedio de esta marca y modelo de vehículo disminuye en aproximadamente\(2.05\) unidades (aproximadamente\(\$2,050\)).
-
Ya que no sabemos nada del automóvil que no sea su antigüedad, asumimos que es de valor aproximadamente promedio y utilizamos el valor promedio de todos los vehículos de cuatro años de esta marca y modelo como nuestra estimación. El valor promedio es simplemente el valor de\(\hat{y}\) obtenido cuando\(4\) se inserta el número para\(x\) en la ecuación de regresión de mínimos cuadrados:\[\hat{y}=−2.05(4)+32.83=24.63\] que corresponde a\(\$24,630\).
-
Ahora\(x=20\) insertamos en la ecuación de regresión de mínimos cuadrados, para obtener\[\hat{y}=−2.05(20)+32.83=−8.17\] cuál corresponde a\(-\$8,170\). Algo está mal aquí, ya que un negativo no tiene sentido. El error surgió de aplicar la ecuación de regresión a un valor de\(x\) no en el rango\(x\) de valores en los datos originales, de dos a seis años. Aplicar la ecuación de regresión\(\bar{y}=\hat{\beta _1}x+\hat{\beta _0}\) a un valor\(x\) fuera del rango de\(x\) -valores en el conjunto de datos se llama extrapolación. Es un uso inválido de la ecuación de regresión y debe evitarse.
- El precio de un vehículo nuevo de esta marca y modelo es el valor del automóvil a la edad\(0\). Si el valor\(x=0\) se inserta en la ecuación de regresión el resultado es siempre\(\hat{\beta _0}\), la\(y\) -intercepción, en este caso\(32.83\), que corresponde a\(\$32,830\). Pero este es un caso de extrapolación, así como lo fue la parte (f), de ahí que este resultado no sea válido, aunque no obviamente así. En el contexto del problema, ya que los automóviles tienden a perder valor mucho más rápidamente inmediatamente después de ser comprados que después de tener varios años de antigüedad, el número\(\$32,830\) es probablemente una subestimación del precio de un automóvil nuevo de esta marca y modelo.
Para énfasis destacamos los puntos planteados por las partes (f) y (g) del ejemplo.
Definición: extrapolación
El proceso de usar la ecuación de regresión de mínimos cuadrados para estimar el valor de\(y\) a un valor de\(x\) que no se encuentra en el rango de los\(x\) valores -en el conjunto de datos que se utilizó para formar la línea de regresión se denomina extrapolación. Se trata de un uso inválido de la ecuación de regresión que puede dar lugar a errores, de ahí que se deba evitar.
La Suma de los Errores Cuadrados SSE
En general, para medir la bondad de ajuste de una línea a un conjunto de datos, debemos calcular el\(y\) valor predicho\(\hat{y}\) en cada punto del conjunto de datos, calcular cada error, cuadrarlo y luego sumar todos los cuadrados. En el caso de la línea de regresión de mínimos cuadrados, sin embargo, la línea que mejor se ajuste a los datos, la suma de los errores al cuadrado se puede calcular directamente a partir de los datos utilizando la siguiente fórmula
La suma de los errores al cuadrado para la línea de regresión de mínimos cuadrados se denota por\(SSE\). Se puede calcular usando la fórmula
\[SSE=SS_{yy}−\hat{β}_1SS_{xy}\]
Ejemplo\(\PageIndex{4}\)
Encuentra la suma de los errores al cuadrado\(SSE\) para la línea de regresión de mínimos cuadrados para el conjunto de datos de cinco puntos
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array}\]
Hazlo de dos maneras:
- utilizando la definición\(\sum (y-\hat{y})^2\);
- usando la fórmula\(SSE=SS_{yy}-\hat{\beta }_1SS_{xy}\).
Solución:
- La línea de regresión de mínimos cuadrados se computó en “Ejemplo\(\PageIndex{2}\)" y es\(\hat{y}=0.34375x-0.125\). Se encontró SSE al final de ese ejemplo usando la definición\(\sum (y-\hat{y})^2\). Los cómputos se tabularon en la Tabla\(\PageIndex{2}\). SSE es la suma de los números en la última columna, que es\(0.75\).
- Los números\(SS_{xy}\) y ya\(\hat{\beta _1}\) se computaron en “Ejemplo\(\PageIndex{2}\)" en el proceso de búsqueda de la línea de regresión de mínimos cuadrados. Así fue el número\(\sum y=9\). Debemos computar\(SS_{yy}\). Para ello es necesario computar primero\[\sum y^2=0+1^2+2^2+3^2+3^2=23\] Luego\[SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=23-\frac{1}{5}(9)^2=6.8\] para que\[SSE=SS_{yy}-\hat{\beta _1}SS_{xy}=6.8-(0.34375)(17.6)=0.75\]
Ejemplo\(\PageIndex{5}\)
Encuentra la suma de los errores al cuadrado\(SSE\) para la línea de regresión de mínimos cuadrados para el conjunto de datos, presentado en Tabla\(\PageIndex{3}\), sobre edad y valores de vehículos usados en “Ejemplo\(\PageIndex{3}\)”.
Solución:
De “Ejemplo\(\PageIndex{3}\)" ya sabemos que
\[SS_{xy}=-28.7,\; \hat{\beta _1}=-2.05,\; \text{and}\; \sum y=246.3\]
Para computar primero\(SS_{yy}\) computamos
\[\sum y^2=28.7^2+24.8^2+26.0^2+30.5^2+23.8^2+24.6^2+23.8^2+20.4^2+21.6^2+22.1^2=6154.15\]
Entonces
\[SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=6154.15-\frac{1}{10}(246.3)^2=87.781\]
Por lo tanto
\[SSE=SS_{yy}-\hat{\beta _1}SS_{xy}=87.781-(-2.05)(-28.7)=28.946\]
Llave para llevar
- Qué tan bien se ajusta una línea recta a un conjunto de datos se mide por la suma de los errores al cuadrado.
- La línea de regresión de mínimos cuadrados es la línea que mejor se ajusta a los datos. Su pendiente e\(y\) intercepción se calculan a partir de los datos utilizando fórmulas.
- La pendiente\(\hat{\beta _1}\) de la línea de regresión de mínimos cuadrados estima el tamaño y la dirección del cambio medio en la variable dependiente\(y\) cuando la variable independiente\(x\) se incrementa en una unidad.
- La suma de los errores al cuadrado\(SSE\) de la línea de regresión de mínimos cuadrados se puede calcular usando una fórmula, sin tener que computar todos los errores individuales.

