10.5: Inferencias estadísticas Acerca de β1

Última actualización
Guardar como PDF

Page ID: 151165

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Aprender a construir un intervalo de confianza para$β_1$, la pendiente de la línea de regresión poblacional.
Aprender a poner a prueba hipótesis respecto a$β_1$.

El parámetro$β_1$, la pendiente de la línea de regresión poblacional, es de primordial importancia en el análisis de regresión porque da la verdadera tasa de cambio en la media$ E(y)$ en respuesta a un incremento unitario en la variable predictora$x$. Por cada unidad el incremento en$x$ la media de la variable de respuesta$y$ cambia por$β_1$ unidades, aumentando si$β_1>0$ y disminuyendo si$β_1 <0$. Deseamos construir intervalos de confianza$β_1$ y probar hipótesis al respecto.

Intervalos de confianza para$β_1$

La pendiente$\hat{β}_1$ de la línea de regresión de mínimos cuadrados es una estimación puntual de$β_1$. Un intervalo de confianza para$β_1$ viene dado por la siguiente fórmula.

Definición:$100(1-\alpha )%$ Confidence Interval for the Slope $β_1$ of the Population Regression Line

\[ \hat{β}_1 \pm t_{α/2} \dfrac{s_{\epsilon}}{\sqrt{SS_{xx}}}\]

dónde$S_\varepsilon =\sqrt{\frac{SSE}{n-2}}$ y el número de grados de libertad es$df=n-2$.

Deben sostenerse los supuestos enumerados en la Sección 10.3.

Definición: desviación estándar de la muestra de errores

El estadístico$S_\varepsilon $ se denomina desviación estándar de la muestra de errores. Estima la desviación estándar$\sigma$ de los errores en la población de$y$ -valores para cada valor fijo de$x$ (ver Figura 10.3.1).

Ejemplo$\PageIndex{1}$

Construir el intervalo de$95\%$ confianza para la pendiente$β_1$ de la línea de regresión poblacional basado en el conjunto de datos de muestra de cinco puntos

\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber\]

Solución:

La estimación puntual$\hat{β}_1$ de$β_1$ se computó en el Ejemplo 10.4.2 como$\hat{β}_1=0.34375$. En el mismo ejemplo$SS_{xx}$ se encontró que sí$SS_{xx}=51.2$. La suma de los errores al cuadrado$SSE$ se computó en el Ejemplo 10.4.4 como$SSE=0.75$. Por lo tanto

\[S_\varepsilon =\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{0.75}{3}}=0.50 \nonumber\]

Nivel de confianza$\alpha =1-0.95=0.05$ lo$95\%$ significa$\alpha /2=0.025$. De la fila etiquetada$df=3$ en la Figura 7.1.6 obtenemos$t_{0.025}=3.182$. Por lo tanto

\[\hat{\beta _1}\pm t_{\alpha /2}\frac{S_\varepsilon }{\sqrt{SS_{xx}}}=0.34375\pm 3.182\left ( \frac{0.50}{\sqrt{51.2}} \right )=0.34375\pm 0.2223 \nonumber\]

que da el intervalo$(0.1215,0.5661)$. $95\%$Confiamos en que la pendiente$β_1$ de la línea de regresión poblacional es entre$0.1215$ y$0.5661$.

Ejemplo$\PageIndex{2}$

Utilizando los datos de muestra del Cuadro 10.4.3 construir un intervalo de$90\%$ confianza para la pendiente$β_1$ de la línea de regresión poblacional que relaciona la edad y el valor de los automóviles del Ejemplo 10.4.3. Interpretar el resultado en el contexto del problema.

Solución:

La estimación puntual$\hat{β}_1$ de$β_1$ se computó en el Ejemplo 10.4.3, como fue$SS_{xx}$. Sus valores son$\hat{β}_1=-2.05$ y$SS_{xx}=14$. La suma de los errores al cuadrado$SSE$ se computó en el Ejemplo 10.4.5 como$SSE=28.946$. Por lo tanto

\[S_\varepsilon =\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{28.946}{8}}=1.902169814 \nonumber\]

Nivel de confianza$\alpha =1-0.90=0.10$ lo$90\%$ significa$\alpha /2=0.05$. De la fila etiquetada$df=8$ en la Figura 7.1.6 obtenemos$t_{0.05}=1.860$. Por lo tanto

\[\hat{\beta _1}\pm t_{\alpha /2}\frac{S_\varepsilon }{\sqrt{SS_{xx}}}=-2.05\pm 1.860\left ( \frac{1.902169814}{\sqrt{14}} \right )=-2.05\pm 0.95 \nonumber\]

que da el intervalo$(-3.00,-1.10)$. $90\%$Confiamos en que la pendiente$β_1$ de la línea de regresión poblacional es entre$-3.00$ y$-1.10$. En el contexto del problema esto quiere decir que para los vehículos de esta marca y modelo de entre dos y seis años estamos$90\%$ seguros de que por cada año adicional de edad el valor promedio de dicho vehículo disminuye entre$\$1,100$ y$\$3,000$.

Hipótesis de prueba Acerca de β1

Las hipótesis respecto$β_1$ pueden probarse utilizando los mismos procedimientos de cinco pasos, ya sea el enfoque de valor crítico o el enfoque$p$ -valor, que se introdujeron en la Sección 8.1 y Sección 8.3. La hipótesis nula siempre tiene la forma$H_0: \beta _1=B_0$ donde$B_0$ es un número determinado a partir de la enunciación del problema. Las tres formas de la hipótesis alternativa, con la terminología para cada caso, son:

Forma de$H_a$	Terminología
\ (H_a\)” style="text-align:center;” class="lt-stats-546">$H_a: \beta _1<B_0$	Cola izquierda
\ (H_a\)” style="text-align:center;” class="lt-stats-546">$H_a: \beta _1>B_0$	Cola derecha
\ (H_a\)” style="text-align:center;” class="lt-stats-546">$H_a: \beta _1\neq B_0$	Dos colas

El valor cero para$B_0$ es de particular importancia ya que en ese caso lo es la hipótesis nula$H_0: \beta _1=0$, que corresponde a la situación en la que no$x$ es útil para predecir$y$. Porque si$β_1=0$ entonces la línea de regresión poblacional es horizontal, entonces la media$E(y)$ es la misma para cada valor de$x$ y estamos igual de bien en ignorar$x$ completamente y aproximarnos$y$ por su valor promedio. Dadas dos variables$x$ y$y$, la carga de la prueba$x$ es que es útil para predecir$y$, no que no lo sea. Así, la frase “probar si$x$ es útil para la predicción de”$y$, o palabras a tal efecto, significa realizar la prueba

\[H_0: \beta _1=0\; \; \text{vs.}\; \; H_a: \beta _1\neq 0\]

Estadístico de prueba estandarizado para pruebas de hipótesis relativas a la pendiente$β_1$ of the Population Regression Line

\[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}\]

El estadístico de prueba tiene la$t$ distribución de Student con$df=n-2$ grados de libertad.

Deben sostenerse los supuestos enumerados en la Sección 10.3.

Ejemplo$\PageIndex{3}$

Probar, a$2\%$ nivel de significancia, si la variable$x$ es útil para predecir con$y$ base en la información del conjunto de datos de cinco puntos

\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber\]

Solución:

Realizaremos la prueba utilizando el enfoque de valor crítico.

Paso 1. Dado que$x$ es útil para predecir$y$ precisamente cuando la pendiente$β_1$ de la línea de regresión poblacional es distinta de cero, la prueba relevante es\[H_0: \beta _1=0\\ \text{vs.}\\ H_a: \beta _1\neq 0\; \; @\; \; \alpha =0.02 \nonumber\]
Paso 2. El estadístico de prueba es\[T=\frac{\hat{\beta _1}}{S_\varepsilon /\sqrt{SS_{xx}}}\] y tiene la$t$ distribución de Student con$n-2=5-2=3$ grados de libertad.
Paso 3. Del Ejemplo 10.4.1,$β_1=0.34375 $ y$SS_{xx}=51.2$. De “Ejemplo$\PageIndex{1}$ “,$S_\varepsilon =0.50$. Por lo tanto, el valor del estadístico de prueba es\[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}=\frac{0.34375}{0.50/\sqrt{51.2}}=4.919 \nonumber\]
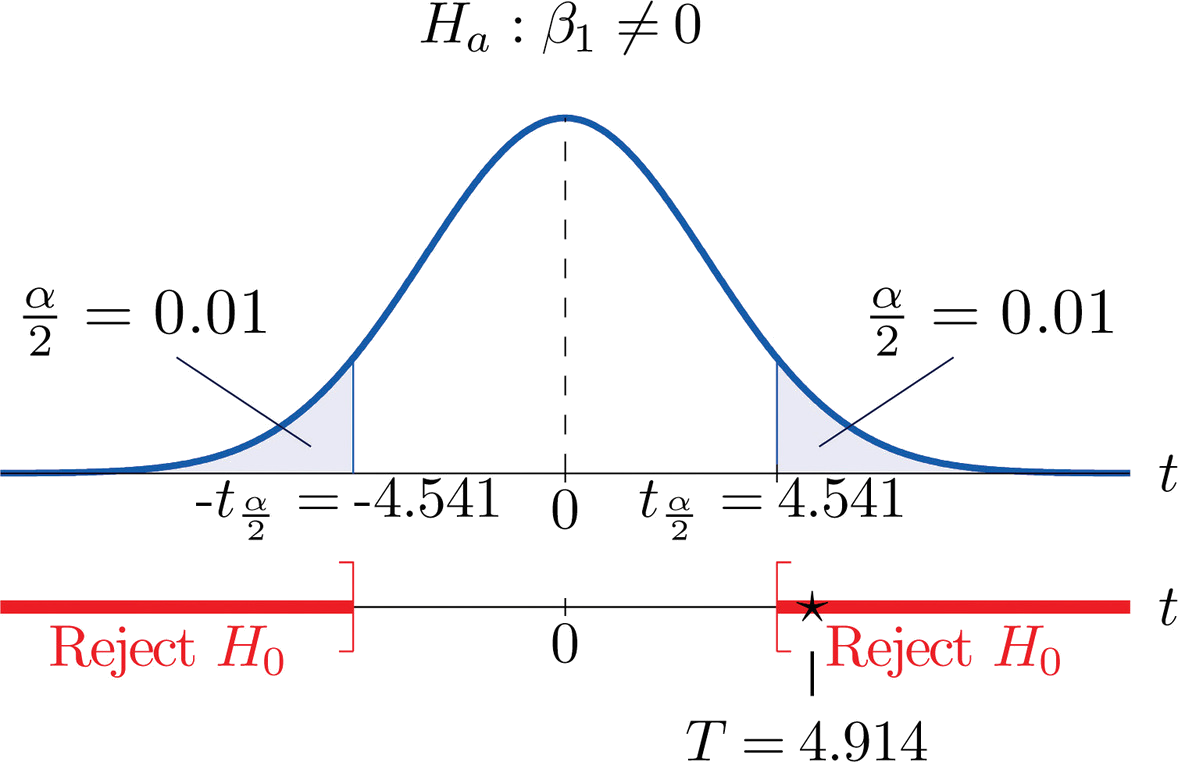
Paso 4. Dado que el símbolo en$H_a$ es “$\neq$” esta es una prueba de dos colas, por lo que hay dos valores críticos$\pm t_{\alpha /2}=\pm t_{0.01}$. Lectura de la línea en la Figura 7.1.6 etiquetada$df=3$,$t_{0.01}=4.541$. La región de rechazo es\[(-\infty ,-4.541]\cup [4.541,\infty ) \nonumber\].
Paso 5. Como se muestra en la Figura$\PageIndex{1}$ “Región de Rechazo y Estadística de Prueba para” el estadístico de prueba cae en la región de rechazo. La decisión es rechazar$H_0$. En el contexto del problema nuestra conclusión es:

Los datos proporcionan evidencia suficiente, a$2\%$ nivel de significancia, para concluir que la pendiente de la línea de regresión poblacional es distinta de cero, por lo que$x$ es útil como predictor de$y$.

alt — Figura$\PageIndex{1}$: Región de rechazo y estadística de prueba por ejemplo$\PageIndex{3}$

Ejemplo$\PageIndex{4}$

Un vendedor de autos afirma que los automóviles de entre dos y seis años de edad de la marca y modelo discutidos en el Ejemplo 10.4.2 pierden más que$\$1,100$ en valor cada año. Pruebe esta afirmación a$5\%$ nivel de significancia.

Solución:

Realizaremos la prueba utilizando el enfoque de valor crítico.

Paso 1. En cuanto a las variables$x$ y$y$, el reclamo del vendedor es que si$x$ se incrementa por$1$ unidad (un año adicional en edad), entonces$y$ disminuye en más de$1.1$ unidades (más de$\$1,100$). Así su aseveración es que la pendiente de la línea de regresión poblacional es negativa, y que es más negativa que$-1.1$. En símbolos,$β_1<-1.1$. Al contener una desigualdad, ésta tiene que ser la hipótesis alternativa. La hipótesis nula tiene que ser una igualdad y tener el mismo número en el lado derecho, por lo que la prueba relevante es\[H_0: \beta _1=-1.1\\ \text{vs.}\\ H_a: \beta _1<-1.1\; \; @\; \; \alpha =0.05 \nonumber\]
Paso 2. El estadístico de prueba es\[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}\] y tiene la$t$ distribución de Student con$8$ grados de libertad.
Paso 3. Del Ejemplo 10.4.2,$β_1=-2.05$ y$SS_{xx}=14$. De “Ejemplo$\PageIndex{2}$ “,$S_\varepsilon =1.902169814$. Por lo tanto, el valor del estadístico de prueba es\[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}=\frac{-2.05-(-1.1)}{1.902169814/\sqrt{14}}=-1.869 \nonumber\]
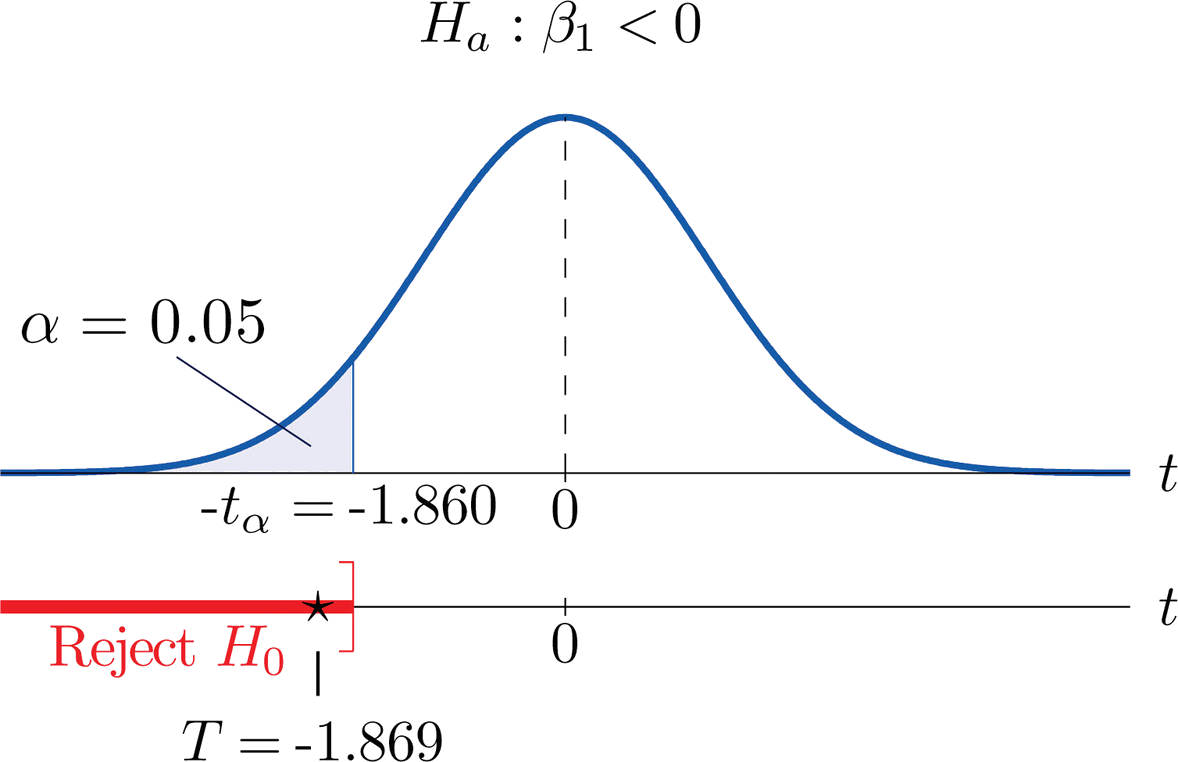
Paso 4. Dado que el símbolo en$H_a$ es “$<$” esta es una prueba de cola izquierda, por lo que hay un solo valor crítico$-t_{\alpha /2}=-t_{0.05}$. Lectura de la línea en la Figura 7.1.6 etiquetada$df=8$,$t_{0.05}=1.860$. La región de rechazo es\[(-\infty ,-1.860] \nonumber\].
Paso 5. Como se muestra en la Figura$\PageIndex{2}$ “Región de Rechazo y Estadística de Prueba para" el estadístico de prueba cae en la región de rechazo. La decisión es rechazar$H_0$. En el contexto del problema nuestra conclusión es:

Los datos proporcionan evidencia suficiente, a$5\%$ nivel de significancia, para concluir que los vehículos de esta marca y modelo y en este rango de edad pierden más de$\$1,100$ por año en valor, en promedio.

alt — Figura$\PageIndex{2}$: Región de rechazo y estadística de prueba para “Ejemplo$\PageIndex{4}$”

Llave para llevar

El parámetro$β_1$, la pendiente de la línea de regresión poblacional, es de interés primario porque describe el cambio promedio$y$ con respecto al incremento unitario en$x$.
El estadístico$\hat{β}_1$, la pendiente de la línea de regresión de mínimos cuadrados, es una estimación puntual de$β_1$. Los intervalos de confianza para se$β_1$ pueden calcular usando una fórmula.
Las hipótesis relativas$β_1$ se prueban utilizando los mismos procedimientos de cinco pasos introducidos en el Capítulo 8.

Intervalos de confianza para\(β_1\)

Hipótesis de prueba Acerca de β1

Llave para llevar