10.6: El coeficiente de determinación
- Page ID
- 151189
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Aprender cuál es el coeficiente de determinación, cómo calcularlo, y qué nos dice sobre la relación entre dos variables\(x\) y\(y\).
Si el diagrama de dispersión de un conjunto de\((x,y)\) pares no muestra ni una tendencia ascendente ni descendente, entonces la línea horizontal le\(\hat{y} =\overline{y}\) ajusta bien, como se ilustra en la Figura\(\PageIndex{1}\). La falta de cualquier tendencia ascendente o descendente significa que cuando un elemento de la población se selecciona al azar, conocer el valor de la medición\(x\) para ese elemento no es útil para predecir el valor de la medición\(y\).
Si el diagrama de dispersión muestra una tendencia lineal hacia arriba o hacia abajo, entonces es útil calcular la línea de regresión de mínimos cuadrados
\[\hat{y} =\hat{β}_1x+\hat{β}_0\]
y utilizarlo en la predicción\(y\). La figura\(\PageIndex{2}\) ilustra esto. En cada panel hemos trazado los datos de altura y peso de la Sección 10.1. Esta es la misma gráfica de dispersión que Figura\(\PageIndex{2}\), con la línea de valor promedio\(\hat{y} =\overline{y}\) superpuesta sobre ella en el panel izquierdo y la línea de regresión de mínimos cuadrados impuesta sobre ella en el panel derecho. Los errores se indican gráficamente por los segmentos de línea vertical.
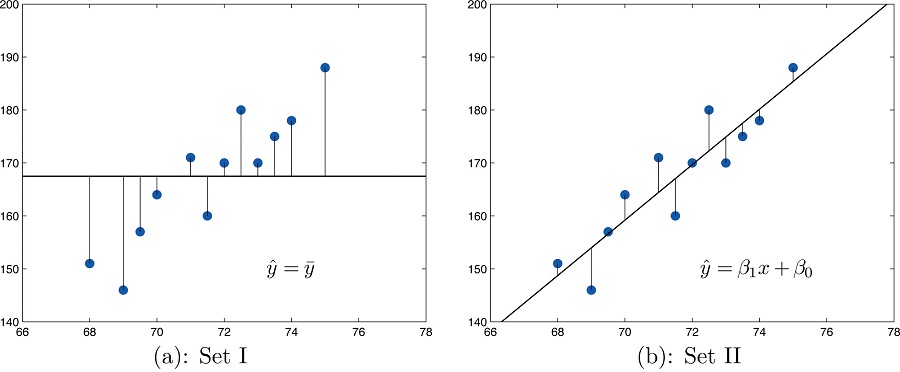
La suma de los errores cuadrados calculados para la línea de regresión,\(SSE\), es menor que la suma de los errores al cuadrado calculados para cualquier otra línea. En particular es menor que la suma de los errores cuadrados calculados usando la línea\(\hat{y}=\overline{y}\), cuya suma es en realidad el número\(SS_{yy}\) que ya hemos visto varias veces. Una medida de lo útil que es usar la ecuación de regresión para la predicción de\(y\) es cuánto menor\(SSE\) es que\(SS_{yy}\). En particular, la proporción de la suma de los errores cuadrados para la línea\(\hat{y} =\overline{y}\) que se elimina al pasar a la línea de regresión de mínimos cuadrados es
Podemos pensar en\(SSE/SS_{yy}\) como la proporción de la variabilidad en\(y\) que no puede ser contabilizada por la relación lineal entre\(x\) y\(y\), ya que sigue ahí incluso cuando\(x\) se toma en cuenta de la mejor manera posible (utilizando la línea de regresión de mínimos cuadrados; recuerde que\(SSE\) es lo más pequeño que puede ser la suma de los errores cuadrados para cualquier línea). Visto en esta luz, el coeficiente de determinación, la proporción complementaria de la variabilidad en\(y\), es la proporción de la variabilidad en todas las\(y\) mediciones que se explica por la relación lineal entre\(x\) y\(y\).
En el contexto de la regresión lineal el coeficiente de determinación es siempre el cuadrado del coeficiente de correlación\(r\) discutido en la Sección 10.2. Así se denota el coeficiente de determinación\(r^2\), y tenemos dos fórmulas adicionales para calcularlo.
Definición: coeficiente de determinación
El coeficiente de determinación de una colección de\((x,y)\) pares es el número\(r^2\) calculado por cualquiera de las siguientes tres expresiones:
Mide la proporción de la variabilidad en\(y\) que se explica por la relación lineal entre\(x\) y\(y\).
Si ya\(r\) se conoce el coeficiente de correlación entonces el coeficiente de determinación puede calcularse simplemente por cuadratura\(r\), como indica la notación,\(r^2=(r)^2\).
Ejemplo\(\PageIndex{1}\)
El valor de los vehículos usados de la marca y modelo discutidos en “Ejemplo 10.4.2" en la Sección 10.4 varía ampliamente. El automóvil más caro de la muestra en el Cuadro 10.4.3 tiene valor\(\$30,500\), que vuelve a ser casi la mitad que el menos costoso, que vale\(\$20,400\). Encontrar la proporción de la variabilidad en el valor que se explica por la relación lineal entre edad y valor.
Solución:
La proporción de la variabilidad en el valor\(y\) que se explica por la relación lineal entre ésta y la edad\(x\) viene dada por el coeficiente de determinación,\(r^2\). Dado que el coeficiente de correlación ya\(r\) se computó en “Ejemplo 10.4.2" en la Sección 10.4 como
\[r=-0.819\\ r^2=(-0.819)2=0.671\]
Acerca\(67\%\) de la variabilidad en el valor de este vehículo puede explicarse por su antigüedad.
Ejemplo\(\PageIndex{2}\)
Utilizar cada una de las tres fórmulas para el coeficiente de determinación para calcular su valor para el ejemplo de edades y valores de vehículos.
Solución:
En “Ejemplo 10.4.2" en la Sección 10.4 calculamos los valores exactos
\[SS_{xx}=14\\ SS_{xy}=-28.7\\ SS_{yy}=87.781\\ \hat{\beta _1}=-2.05\]
En “Ejemplo 10.4.4" en la Sección 10.4 calculamos el valor exacto
\[SSE=28.946\]Insertar estos valores en las fórmulas de la definición, uno tras otro, da
\[r^2=\dfrac{SS_{yy}−SSE}{SS_{yy}}=\dfrac{87.781−28.946}{87.781}=0.6702475479\]
\[r^2= \dfrac{SS^2_{xy}}{SS_{xx}SS_{yy}}=\dfrac{(−28.7)^2}{(14)(87.781)}=0.6702475479\]
\[r^2=\hat{β}_1 \dfrac{SS_{xy}}{SS_{yy}}=−2.05\dfrac{−28.7}{87.781}=0.6702475479\]que redondea a\(0.670\). La discrepancia entre el valor aquí y en el ejemplo anterior se debe a que allí se utilizó un valor redondeado\(r\) de “Ejemplo 10.4.2". El valor real de\(r\) antes del redondeo es\(0.8186864772\), que al cuadrado da el valor para\(r^2\) obtenido aquí.
El coeficiente de determinación siempre se\(r^2\) puede calcular al cuadrado del coeficiente de correlación\(r\) si se conoce. También se puede utilizar cualquiera de las fórmulas definitorias. Normalmente se tomaría la elección en función de qué cantidades ya se han calculado. Lo que se debe evitar es tratar de calcular\(r\) tomando la raíz cuadrada de\(r^2\), si ya se sabe, ya que es fácil hacer un error de señal de esta manera. Para ver qué puede salir mal, supongamos\(r^2=0.64\). Tomar la raíz cuadrada de un número positivo con cualquier dispositivo calculador siempre devolverá un resultado positivo. La raíz cuadrada de\(0.64\) es\(0.8\). Sin embargo, el valor real de\(r\) podría ser el número negativo\(-0.8\).
Llave para llevar
- El coeficiente de determinación\(r^2\) estima la proporción de la variabilidad en la variable\(y\) que se explica por la relación lineal entre\(y\) y la variable\(x\).
- Existen varias fórmulas para la computación\(r^2\). La elección de cuál usar puede basarse en qué cantidades ya se han calculado hasta el momento.

