11.2: Pruebas de bondad de ajuste de una muestra de Chi-Cuadrado
- Page ID
- 151156
Objetivos de aprendizaje
- Comprender cómo usar una prueba de chi-cuadrado para juzgar si una muestra se ajusta bien a una población en particular.
Supongamos que deseamos determinar si un dado de seis lados de aspecto ordinario es justo, o equilibrado, lo que significa que cada cara tiene probabilidad\(1/6\) de aterrizar en la parte superior cuando se arroja el dado. Podríamos arrojar el dado decenas, tal vez cientos, de veces y comparar el número real de veces que cada cara aterrizó encima con el número esperado, que sería\(1/6\) del número total de lanzamientos. No esperaríamos que cada número fuera exactamente\(1/6\) del total, pero debería estar cerca. Para ser específicos, supongamos que el dado es\(n=60\) tiempos de lanzamiento con los resultados resumidos en la Tabla\(\PageIndex{1}\). Para facilidad de referencia añadimos una columna de frecuencias esperadas, que en este sencillo ejemplo es simplemente una columna de\(10s\). El resultado se muestra como Tabla\(\PageIndex{2}\). En analogía con el apartado anterior llamamos a esto una tabla “actualizada”. Una medida de cuánto se desvían los datos de lo que esperaríamos ver si el dado realmente fuera justo es la suma de los cuadrados de las diferencias entre la frecuencia observada\(O\) y la frecuencia esperada\(E\) en cada fila, o, estandarizando dividiendo cada cuadrado por el número esperado, la suma
\[\dfrac{Σ(O−E)^2}{E}\]
Si formulamos la investigación como prueba de hipótesis, la prueba es
\[H_0: \text{The die is fair}\\ vs.\\ H_a: \text{The die is not fair}\]
| Valor de la matriz | Distribución Sumida | Frecuencia Observada |
|---|---|---|
| \(1\) | \(1/6\) | \(9\) |
| \(2\) | \(1/6\) | \(15\) |
| \(3\) | \(1/6\) | \(9\) |
| \(4\) | \(1/6\) | \(8\) |
| \(5\) | \(1/6\) | \(6\) |
| \(6\) | \(1/6\) | \(13\) |
| Valor de la matriz | Distribución Sumida | Freq observado. | Se espera Freq. |
|---|---|---|---|
| \(1\) | \(1/6\) | \(9\) | \(10\) |
| \(2\) | \(1/6\) | \(15\) | \(10\) |
| \(3\) | \(1/6\) | \(9\) | \(10\) |
| \(4\) | \(1/6\) | \(8\) | \(10\) |
| \(5\) | \(1/6\) | \(6\) | \(10\) |
| \(6\) | \(1/6\) | \(13\) | \(10\) |
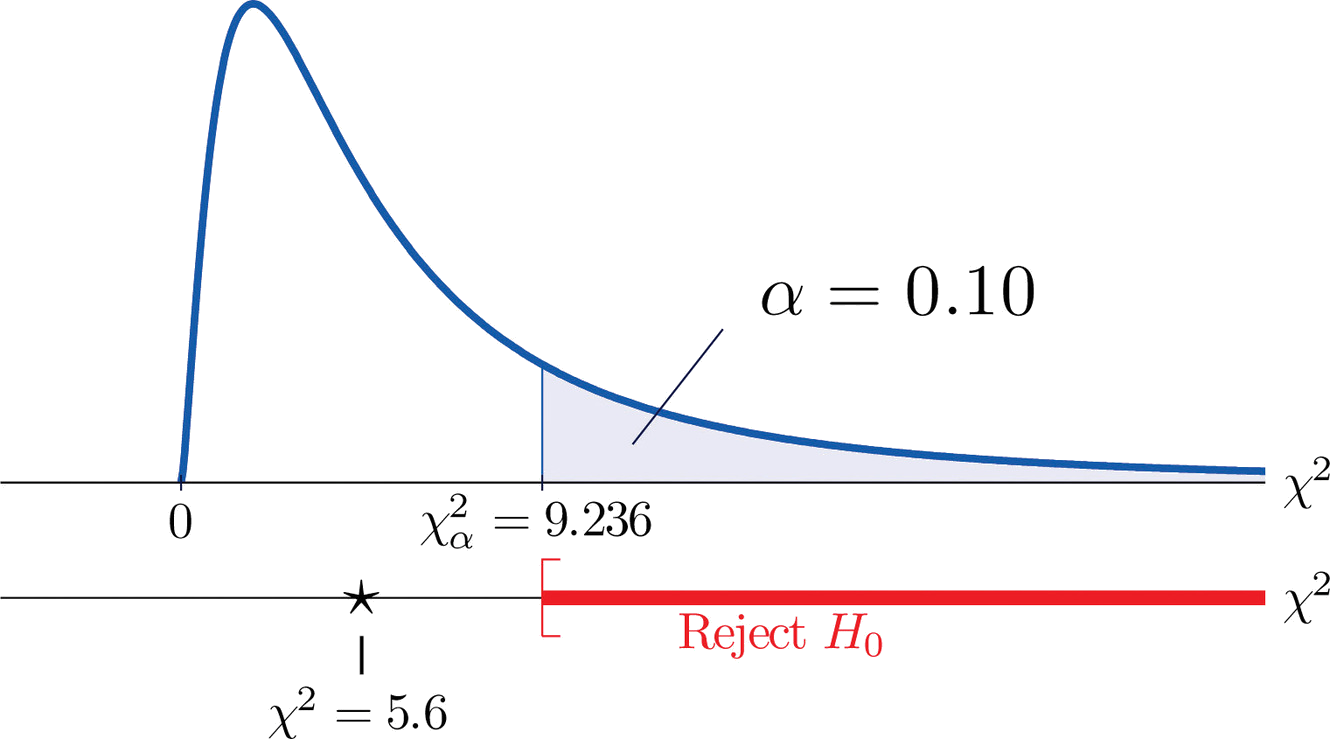
Rechazaríamos la hipótesis nula de que el dado es justo solo si el número\(\dfrac{Σ(O−E)^2}{E}\) es grande, por lo que la prueba es de cola derecha. En este ejemplo la variable aleatoria\(\dfrac{Σ(O−E)^2}{E}\) tiene la distribución chi-cuadrada con cinco grados de libertad. Si hubiéramos decidido desde el principio probar en el\(10\%\) nivel de significancia, el valor crítico que define la región de rechazo sería, leyendo de la Figura 7.1.6,\(\chi _{\alpha }^{2}=\chi _{0.10}^{2}=9.236\), de manera que la región de rechazo sería el intervalo\[[9.236,\infty )\]. Cuando calculamos el valor del estadístico de prueba estandarizado usando los números en las dos últimas columnas de Table\(\PageIndex{2}\), obtenemos
\[\begin{align*} \sum \frac{(O-E)^2}{E} &= \frac{(-1)^2}{10}+\frac{(5)^2}{10}+\frac{(-1)^2}{10}+\frac{(-2)^2}{10}+\frac{(-4)^2}{10}+\frac{(3)^2}{10}\\ &= 0.1+2.5+0.1+0.4+1.6+0.9\\ &= 5.6 \end{align*}\]
Ya que\(5.6<9.236\) la decisión no es rechazar\(H_0\). Ver Figura\(\PageIndex{1}\). Los datos no aportan evidencia suficiente, a\(10\%\) nivel de significancia, para concluir que el dado está cargado.
En la situación general consideramos una variable aleatoria discreta que puede tomar\(I\) diferentes valores,\(x_1,\: x_2,\cdots ,x_I\), para lo cual la suposición predeterminada es que la distribución de probabilidad es
\[\begin{array}{c|c c c c} x & x_1 & x_2 & \cdots & x_I \\ \hline P(x) &p_1 &p_2 &\cdots &p_I\\ \end{array}\]
Deseamos probar las hipótesis:
\[H_0: \text{The assumed probability distribution for X is valid}\\ vs.\\ H_a: \text{The assumed probability distribution for X is not valid}\]
Tomamos una muestra de tamaño\(n\) y obtenemos una lista de frecuencias observadas. Esto se muestra en la Tabla\(\PageIndex{3}\). Con base en la distribución de probabilidad supuesta también tenemos una lista de frecuencias supuestas, cada una de las cuales se define y calcula mediante la fórmula
\[Ei=n×pi\]
| Niveles de factores | Distribución Sumida | Frecuencia Observada |
|---|---|---|
| \(1\) | \(p_1\) | \(O_1\) |
| \(2\) | \(p_2\) | \(O_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O_I\) |
Tabla\(\PageIndex{3}\) se actualiza a Tabla\(\PageIndex{4}\) sumando la frecuencia esperada para cada valor de\(X\). Para simplificar la notación bajamos índices para las frecuencias observadas y esperadas y representamos Tabla\(\PageIndex{4}\) por Tabla\(\PageIndex{5}\).
| Niveles de factores | Distribución Sumida | Freq observado. | Se espera Freq. |
|---|---|---|---|
| \(1\) | \(p_1\) | \(O_1\) | \(E_1\) |
| \(2\) | \(p_2\) | \(O_2\) | \(E_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O_I\) | \(E_I\) |
| Niveles de factores | Distribución Sumida | Freq observado. | Se espera Freq. |
|---|---|---|---|
| \(1\) | \(p_1\) | \(O\) | \(E\) |
| \(2\) | \(p_2\) | \(O\) | \(E\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O\) | \(E\) |
Aquí está el estadístico de prueba para la hipótesis general basada en Tabla\(\PageIndex{5}\), junto con las condiciones de que sigue una distribución chi-cuadrada.
Estadística de prueba para probar la bondad de ajuste a una distribución de probabilidad discreta
\[\chi ^2 =\sum \frac{(O-E)^2}{E}\]
donde la suma está sobre todas las filas de la tabla (una por cada valor de\(X\)).
Si
- la verdadera distribución de probabilidad de\(X\) es como se supone, y
- el recuento observado\(O\) de cada celda en la Tabla\(\PageIndex{5}\) es al menos\(5\),
luego\(\chi ^2\) aproximadamente sigue una distribución chi-cuadrada con\(df=I-1\) grados de libertad.
La prueba se conoce como prueba de bondad de ajuste ya que\(\chi ^2\) prueba la hipótesis nula de que la muestra se ajusta bien a la distribución de probabilidad asumida. Siempre es de cola derecha, ya que la desviación de la distribución de probabilidad supuesta corresponde a grandes valores de\(\chi ^2\).
Las pruebas se realizan utilizando cualquiera de los procedimientos habituales de cinco pasos.
Ejemplo\(\PageIndex{1}\)
En la tabla se\(\PageIndex{6}\) muestra la distribución de diversos grupos étnicos en la población de un estado en particular con base en un censo decenal de Estados Unidos. Cinco años después se tomó una muestra aleatoria de\(2,500\) residentes del estado, con los resultados dados en la Tabla\(\PageIndex{7}\) (junto con la distribución de probabilidad del año censal). Pruebe, a\(1\%\) nivel de significancia, si existe evidencia suficiente en la muestra para concluir que la distribución de los grupos étnicos en este estado cinco años después del censo había cambiado con respecto a la del año censal.
| Etnicidad | Blanco | Negro | Amer. -Indio | Hispano | Asiático | Otros |
|---|---|---|---|---|---|---|
| Proporción | \(0.743\) | \(0.216\) | \(0.012\) | \(0.012\) | \(0.008\) | \(0.009\) |
| Etnicidad | Distribución Sumida | Frecuencia Observada |
|---|---|---|
| Blanco | \(0.743\) | \(1732\) |
| Negro | \(0.216\) | \(538\) |
| Americano-indio | \(0.012\) | \(32\) |
| Hispano | \(0.012\) | \(42\) |
| Asiático | \(0.008\) | \(133\) |
| Otros | \(0.009\) | \(23\) |
Solución:
Probamos usando el enfoque de valor crítico.
- Paso 1. Las hipótesis de interés en este caso pueden expresarse como\[H_0: \text{The distribution of ethnic groups has not changed}\\ vs.\\ H_a: \text{The distribution of ethnic groups has changed}\]
- Paso 2. La distribución es chi-cuadrada.
- Paso 3. Para calcular el valor del estadístico de prueba primero debemos calcular el número esperado para cada fila de Table\(\PageIndex{7}\). Dado que\(n=2500\), usando la fórmula\(E_i=n\times p_i\) y los valores\(p_i\) de cualquiera de Tabla\(\PageIndex{6}\) o Tabla\(\PageIndex{7}\),\[E_1=2500×0.743=1857.5\\ E_2=2500×0.216=540\\ E_3=2500×0.012=30\\ E_4=2500×0.012=30\\ E_5=2500×0.008=20\\ E_6=2500×0.009=22.5\]
La tabla\(\PageIndex{7}\) se actualiza a Tabla\(\PageIndex{8}\).
| Etnicidad | Supuesto Dist. | Freq observado. | Se espera Freq. |
|---|---|---|---|
| Blanco | \(0.743\) | \(1732\) | \(1857.5\) |
| Negro | \(0.216\) | \(538\) | \(540\) |
| Americano-indio | \(0.012\) | \(32\) | \(30\) |
| Hispano | \(0.012\) | \(42\) | \(30\) |
| Asiático | \(0.008\) | \(133\) | \(20\) |
| Otros | \(0.009\) | \(23\) | \(22.5\) |
El valor del estadístico de prueba es
\[\begin{align*} \chi ^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(1732-1857.5)^2}{1857.5}+\frac{(538-540)^2}{540}+\frac{(32-30)^2}{30}+\frac{(42-30)^2}{30}+\frac{(133-20)^2}{20}+\frac{(23-22.5)^2}{22.5}\\ &= 651.881 \end{align*}\]
Dado que la variable aleatoria toma seis valores,\(I=6\). Así, el estadístico de prueba sigue la distribución de chi-cuadrado con\(df=6-1=5\) grados de libertad.
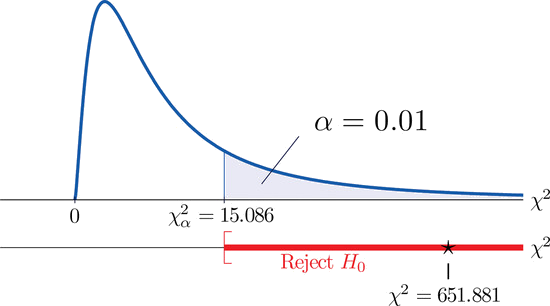
Dado que la prueba es de cola derecha, el valor crítico es\(\chi _{0.01}^{2}\). Al leer de la Figura 7.1.6,\(\chi _{0.01}^{2}=15.086\), así lo es la región de rechazo\([15.086,\infty )\).
Ya que\(651.881>15.086\) la decisión es rechazar la hipótesis nula. Ver Figura\(\PageIndex{2}\). Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que la distribución étnica en este estado ha cambiado en los cinco años transcurridos desde el censo de Estados Unidos.
Llave para llevar
- La prueba de bondad de ajuste de chi-cuadrado se puede utilizar para evaluar la hipótesis de que una muestra se toma de una población con una distribución de probabilidad específica asumida.

