6.1: Análisis de Correlación

Para comenzar con las relaciones, primero se necesita encontrar una correlación, por ejemplo, medir la extensión y el signo de la relación, y probar si esto es estadísticamente confiable.

Obsérvese que la correlación no refleja la naturaleza de la relación (Figura\(\PageIndex{1}\)). Si encontramos una correlación significativa entre variables, esto podría significar que A depende de B, B depende de A, A y B dependen entre sí, o A y B dependen de una tercera variable C pero no tienen relación entre sí. Un ejemplo famoso es la correlación entre la venta de helados y los incendios en el hogar. Sería extraño sugerir que comer helado hace que la gente inicie incendios, o que experimentar incendios haga que la gente compre helado. De hecho, ambos parámetros dependen de la temperatura del aire\(^{[1]}\).

Figura\(\PageIndex{1}\) Correlación y causalidad (tomada de XKCD, http://xkcd.com/552/).

Los números por sí solos podrían ser engañosos, así que hay una regla simple: trazarlo primero.

Trazarlo primero

El ejemplo más llamativo de relaciones donde los números por sí solos hacen para proporcionar una respuesta confiable, es el cuarteto de Anscombe, cuatro conjuntos de dos variables que tienen medias y desviaciones estándar casi idénticas:

Código\(\PageIndex{1}\) (R):

classic.desc <- function(.x) {c(mean=mean(.x, na.rm=TRUE),var=var(.x, na.rm=TRUE))}
sapply(anscombe, classic.desc)

(Data anscombe está incrustado en R. Para compactar entrada y salida, se utilizaron varios trucos. Por favor encuéntralos tú mismo.)

Los coeficientes del modelo lineal (ver abajo) también son bastante similares pero si trazamos estos datos, la imagen (Figura\(\PageIndex{2}\)) es radicalmente diferente de lo que se refleja en números:

Código\(\PageIndex{2}\) (R):

a.vars <- data.frame(i=c(1, 5), ii=c(2, 6), iii=c(3, 7), iv=c(4, 8))
oldpar <- par(mfrow=c(2, 2), mar=c(4, 4, 1, 1))
for (i in 1:4) { plot(anscombe[a.vars[, i]], pch=19, cex=1.2); abline(lm(anscombe[rev(a.vars[, i])]), lty=2) }

(Para fines estéticos, ponemos las cuatro parcelas en una misma figura. Tenga en cuenta el operador for que produce ciclo repitiendo una secuencia de comandos cuatro veces. Para saber más, ¿revisa?” para”.)

Al crédito de los métodos numéricos no paramétricos y/o robustos, no son tan fáciles de engañar:

Código\(\PageIndex{3}\) (R):

robust.desc <- function(.x) {c(median=median(.x, na.rm=TRUE),IQR=IQR(.x, na.rm=TRUE), mad=mad(.x, na.rm=TRUE))}
sapply(anscombe, robust.desc)

Figura Cuarteto de\(\PageIndex{2}\) Anscombe, trazado junto con líneas de modelos lineales.

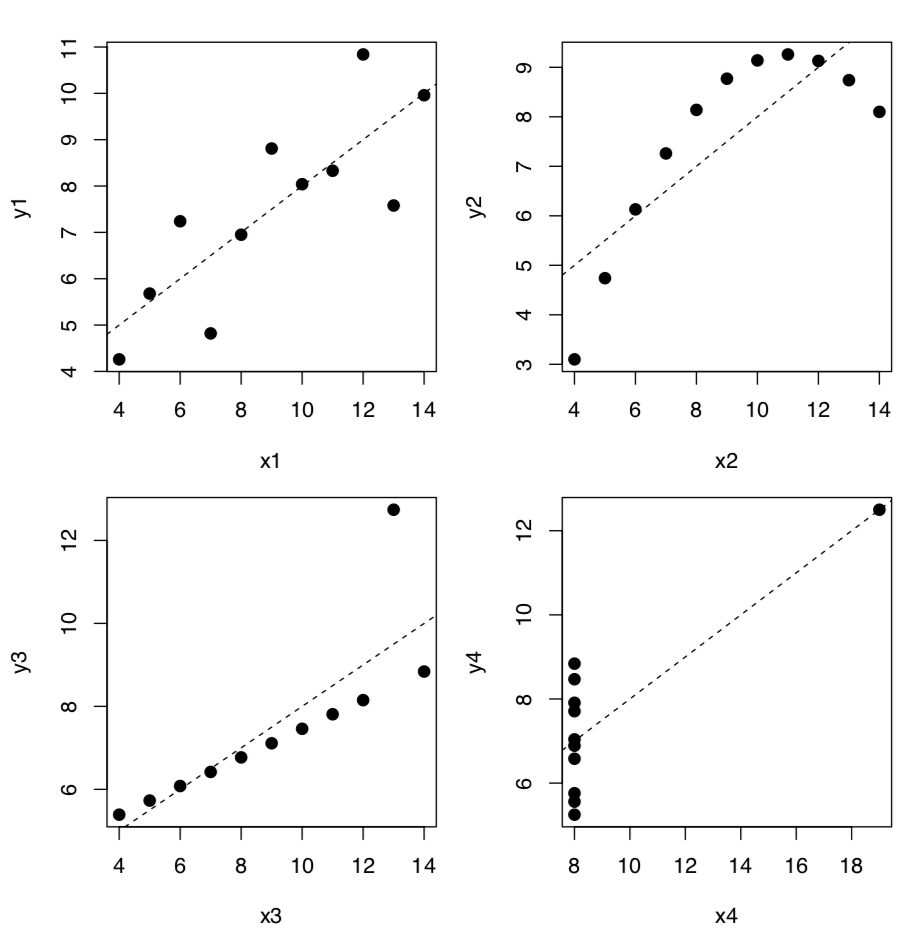
Esto es correcto para adivinar que las gráficas de caja también deben mostrar la diferencia. Por favor, trata de tramarlos tú mismo.

Correlación

Para medir la extensión y el signo de la relación lineal, necesitamos calcular el coeficiente de correlación. El valor absoluto del coeficiente de correlación varía de 0 a 1. Cero significa que los valores de una variable no están conectados con los valores de la otra variable. Un coeficiente de correlación de\(1\) o\(-1\) es una evidencia de una relación lineal entre dos variables. Un valor positivo de medias la correlación es positiva (cuanto mayor sea el valor de una variable, mayor será el valor de la otra), mientras que los valores negativos significan que la correlación es negativa (cuanto mayor sea el valor de una, menor de la otra).

Es fácil calcular el coeficiente de correlación en R:

Código\(\PageIndex{4}\) (R):

cor(5:15, 7:17)
cor(5:15, c(7:16, 23))

(Por defecto, R calcula el coeficiente de correlación paramétrico de Pearson\(r\).)

En el caso más simple, se le dan dos argumentos (vectores de igual longitud). También se puede llamar con un argumento si se usa una matriz o un marco de datos. En este caso, la función cor () calcula una matriz de correlación, compuesta por coeficientes de correlación entre todos los pares de columnas de datos.

Código\(\PageIndex{5}\) (R):

cor(trees)

Como correlación es de hecho el tamaño del efecto de la covarianza, variación conjunta de dos variables, para calcularla manualmente, se necesita conocer varianzas individuales y varianza de la diferencia entre variables:

Código\(\PageIndex{6}\) (R):

with(trees, cor(Girth, Height))
(v1 <- var(trees$Girth))
(v2 <- var(trees$Height))
(v12 <- var(trees$Girth - trees$Height))
(pearson.r <- (v1 + v2 - v12)/(2*sqrt(v1)*sqrt(v2)))

Otra forma es usar la función cov () que calcula la covarianza directamente:

Código\(\PageIndex{7}\) (R):

with(trees, cov(Girth, Height)/(sd(Girth)*sd(Height)))

Para interpretar los valores del coeficiente de correlación, podemos usar las funciones symnum () o Topm () (ver abajo), o Mag () junto con apply ():

Código\(\PageIndex{8}\) (R):

noquote(apply(cor(trees), 1:2, function(.x) Mag(.x, squared=FALSE)))  # asmisc.r

Si los números de observaciones en las columnas son desiguales (algunas columnas tienen datos faltantes), el uso del parámetro se vuelve importante. Por defecto es todo lo que devuelve NA siempre que falten valores en un conjunto de datos. Si el uso del parámetro se establece en completo.obs, las observaciones con datos faltantes se excluyen automáticamente. En ocasiones, los valores de datos faltantes están tan dispersos que completo.obs no dejará mucho de ellos. En ese último caso, use parwise.complete.obs que elimina los valores faltantes par por par.

Los coeficientes de correlación paramétrica de Pearson fallan característicamente con los datos de Anscombe:

Código\(\PageIndex{9}\) (R):

diag(cor(anscombe[, 1:4], anscombe[, 5:8]))

Para superar el problema, se puede usar el coeficiente de correlación no paramétrico de Spearman\(\rho\) (“rho” o coeficiente de correlación de rango) que se usa con mayor frecuencia:

Código\(\PageIndex{10}\) (R):

with(trees, cor(Girth, Height, method="spearman"))
diag(cor(anscombe[, 1:4], anscombe[, 5:8], method="s"))

(¡La correlación de Spearman es definitivamente más robusta!)

El tercer tipo de coeficiente de correlación en R es no paramétrico de Kendall\(\tau\) (“tau”):

Código\(\PageIndex{11}\) (R):

with(trees, cor(Girth, Height, method="k"))
diag(cor(anscombe[, 1:4], anscombe[, 5:8], method="k"))

A menudo se utiliza para medir la asociación entre dos variables clasificadas o binarias, es decir, como alternativa a los tamaños de efecto de la asociación en tablas de contingencia.

¿Cómo verificar si la correlación es estadísticamente significativa? Como hipótesis nula, podríamos aceptar que el coeficiente de correlación es igual a cero (sin correlación). Si se rechaza el nulo, entonces la correlación es significativa:

Código\(\PageIndex{12}\) (R):

with(trees, cor.test(Girth, Height))

La lógica de cor.test () es la misma que en las pruebas anteriores (Cuadro 5.1.1, Figura 5.1.1). En términos de valor p:

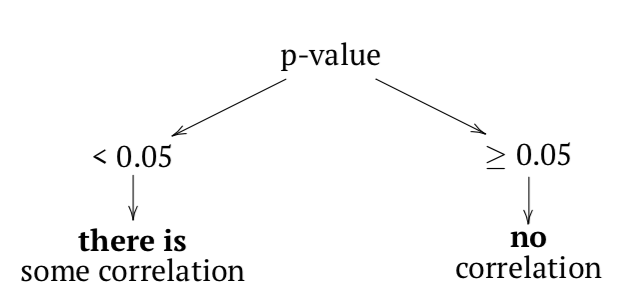
La probabilidad de obtener el estadístico de prueba (coeficiente de correlación), dado el supuesto inicial de correlación cero entre los datos es muy baja, aproximadamente 0.3%. Rechazaríamos H\(_0\) y por lo tanto aceptaríamos una hipótesis alternativa de que la correlación entre variables está presente. Tenga en cuenta el intervalo de confianza, indica aquí que el valor verdadero del coeficiente se encuentra entre 0.2 y 0.7. con 95% de probabilidad.

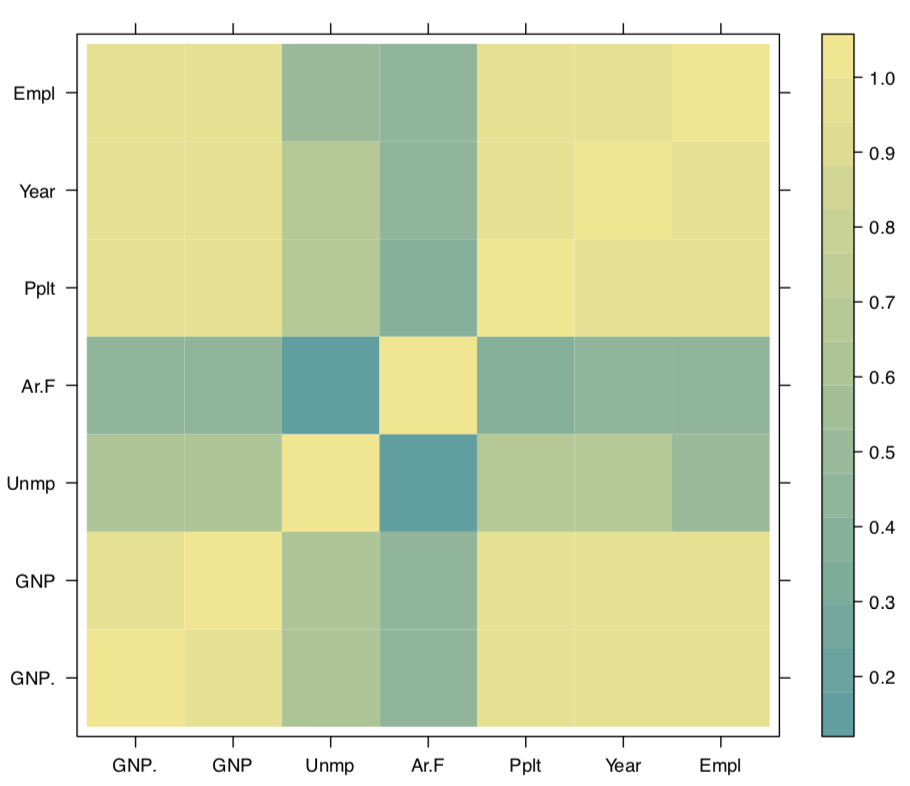
No siempre es fácil leer la tabla de correlación grande, como en el siguiente ejemplo de datos macroeconómicos longley. Afortunadamente, hay varias soluciones alternativas, por ejemplo, la función symnum () que reemplaza los números con letras o símbolos de acuerdo a su valor:

Código\(\PageIndex{13}\) (R):

symnum(cor(longley))

La segunda forma es representar la matriz de correlación con una gráfica. Por ejemplo, podemos usar el mapa de calor: dividir todo de\(-1\) a\(+1\) en intervalos iguales, asignar el color para cada intervalo y mostrar estos colores (Figura\(\PageIndex{3}\)):

Código\(\PageIndex{14}\) (R):

cor.l <- cor(longley)
dimnames(cor.l) <- lapply(dimnames(cor.l), abbreviate)
rgb.palette <- colorRampPalette(c("cadetblue", "khaki"))
palette.l <- rgb.palette(length(unique(abs(cor.l))))
library(lattice)
levelplot(abs(cor.l), col.regions=palette.l, xlab="", ylab="")

(Acortamos aquí los nombres largos con el comando abbreviate ().)

La otra forma interesante de representar correlaciones son elipses de correlación (a partir del paquete de elipse). En ese caso, los coeficientes de correlación se muestran como elipses comprimidas de diversas maneras; cuando el coeficiente está cerca\(-1\) o\(+1\), la elipse es más estrecha (Figura\(\PageIndex{4}\)). La pendiente de la elipse representa el signo de correlación (negativa o positiva):

Código\(\PageIndex{15}\) (R):

library(ellipse)
colors <- cm.colors(7)
plotcorr(cor.l, type="lower", col=colors[5*cor.l + 2])

Varias formas útiles de visualizar y analizar las correlaciones presentes en el archivo asmisc.r suministrado con este libro:

Código\(\PageIndex{16}\) (R):

tox <- read.table("data/poisoning.txt", h=TRUE)
tox.cor <- cor(tox, method="k")
Pleiad(tox.cor, corr=TRUE, lcol="black") # asmisc.r

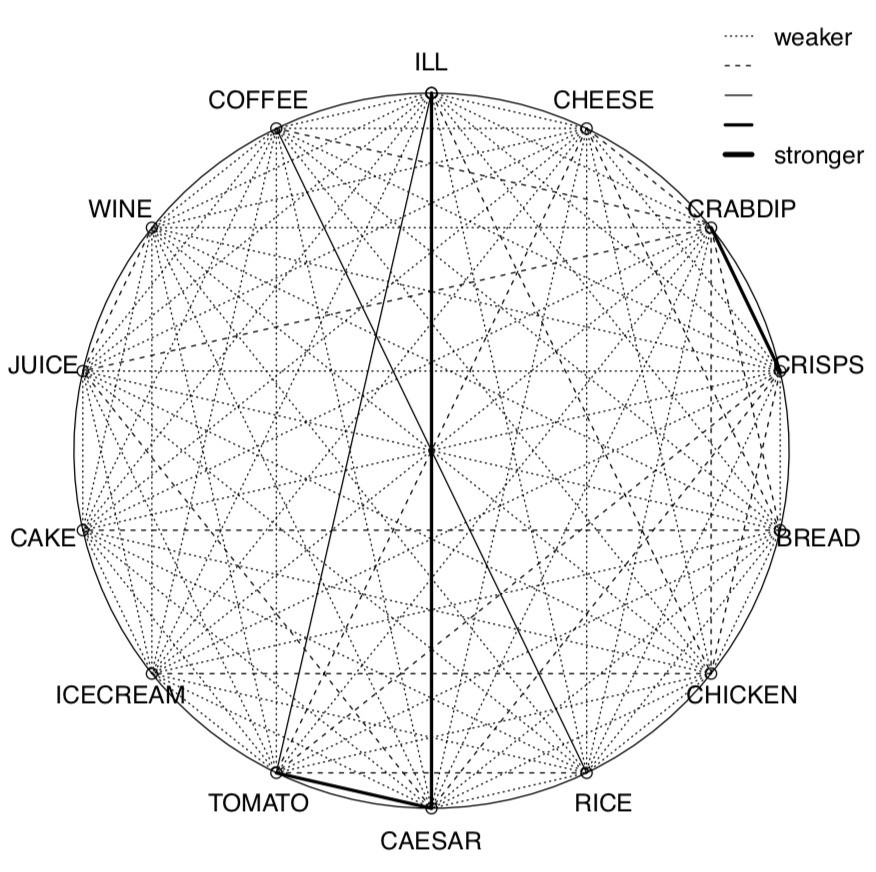
Calculamos aquí el coeficiente de correlación de Kendall para los datos binarios de toxicidad para hacer la imagen utilizada en la página de título. La pleíada () no solo mostró (Figura\(\PageIndex{5}\)) que la enfermedad se asocia con tomate y ensalada César, sino que también encontró otras dos pleíadas de correlación: café/arroz y cangrejo dip/papas fritas. (Por cierto, las pléyadas muestran una aplicación más de R: análisis de redes.)

Figura\(\PageIndex{3}\) Mapa de calor: representación gráfica de la matriz de correlación.

La función Cor () genera matriz de correlación junto con asteriscos para las pruebas de correlación significativas:

Código\(\PageIndex{17}\) (R):

tox <- read.table("data/poisoning.txt", h=TRUE)
Cor(tox, method="kendall", dec=2) # asmisc.r

Figura Coeficientes de\(\PageIndex{4}\) correlación como elipses.

Finalmente, la función Topm () muestra las correlaciones más grandes por filas:

Código\(\PageIndex{18}\) (R):

tox <- read.table("data/poisoning.txt", h=TRUE)
tox.cor <- cor(tox, method="k")
Topm(tox.cor, level=0.4) # asmisc.r

El archivo de datos traits.txt contiene los resultados de la encuesta donde se registraron la mayoría de los caracteres de fenotipo humano genéticamente aparentes de muchos individuos. La explicación de estos caracteres se encuentran en el archivo trait_c.txt. Analice estos datos con métodos de correlación.

Figura Pleiads de\(\PageIndex{5}\) correlación para los datos de toxicidad.

Referencias

1. Existen, sin embargo, técnicas avanzadas con el objetivo de entender la diferencia entre causalidad y correlación: por ejemplo, las implementadas en el paquete bnlearn.