6.2: Análisis de regresión

Una sola línea

El análisis de correlación permite determinar si las variables son dependientes y calcular la fuerza y el signo de la dependencia. Sin embargo, si el objetivo es comprender las otras características de la dependencia (como dirección), y, aún más importante, predecir (extrapolar) resultados (Figura\(\PageIndex{1}\)) necesitamos otro tipo de análisis, el análisis de regresión.

\(\PageIndex{1}\)Extrapolación de Figura (tomada de XKCD, http://xkcd.com/605/).

Da mucha más información sobre la relación, pero nos obliga a asignar variables de antemano a una de dos categorías: influencia (predictor) o respuesta. Este enfoque se basa en la naturaleza de los datos: por ejemplo, podemos usar la temperatura del aire para predecir las ventas de helados, pero difícilmente al revés.

El ejemplo más conocido es una regresión lineal simple:

\(\mbox{response} = \mbox{intercept} + \mbox{slope}\times\mbox{influence}\)

o, en lenguaje de fórmula R, aún más simple:

respuesta ~ influencia

Ese modelo estima el valor promedio de respuesta si se conoce el valor de influencia (nótese que tanto el efecto como la influencia son variables de medición). Las diferencias entre los valores observados y los predichos son errores del modelo (o, mejor, residuales). El objetivo es minimizar los residuos (Figura\(\PageIndex{3}\)); dado que los residuos pueden ser tanto positivos como negativos, normalmente se realiza a través de valores al cuadrado, este método se denomina mínimos cuadrados.

Idealmente, los residuos deben tener la distribución normal con media cero y varianza constante que no depende del efecto y la influencia. En ese caso, los residuos son homogéneos. En otros casos, los residuos podrían mostrar heterogeneidad. Y si existe la dependencia entre los residuos y la influencia, entonces lo más probable es que el modelo general sea no lineal y por lo tanto requiera el otro tipo de análisis.

El modelo de regresión lineal se basa en los diversos supuestos:

• Linealidad de la relación. Significa que para un cambio de unidad en la influencia, siempre debe haber un cambio correspondiente en efecto. Las unidades de cambio en la variable de respuesta deben conservar el mismo tamaño y signo en todo el rango de influencia.
• Normalidad de los residuos. ¡Tenga en cuenta que la normalidad de los datos no es una suposición! Sin embargo, si quieres deshacerte de la mayoría de las otras suposiciones, es posible que quieras usar otros métodos de regresión como LOESS.
• Homocedasticidad de residuos. La variabilidad dentro de los residuos debe permanecer constante en todo el rango de influencia, o de lo contrario no podríamos predecir el efecto de manera confiable.

La hipótesis nula establece que nada en la variabilidad de respuesta se explica por el modelo. Numéricamente, el coeficiente R-cuadrado es el grado en que la variabilidad de respuesta es explicada por el modelo, por lo tanto, la hipótesis nula es que R-cuadrado es igual a cero, este enfoque utiliza estadísticas F (estadísticas de Fisher), como en ANOVA. También hay comprobaciones de hipótesis nulas adicionales de que tanto la intercepción como la pendiente son ceros. Si los tres valores p son menores que el nivel de significancia (0.05), todo el modelo es estadísticamente significativo.

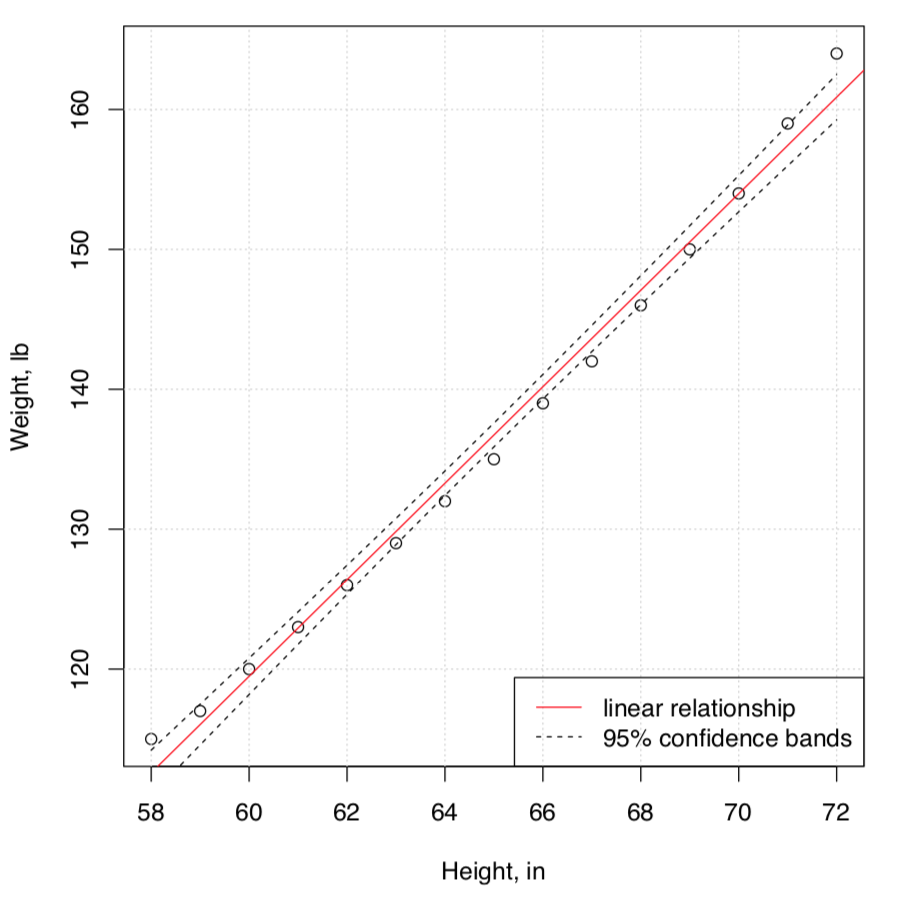
Aquí hay un ejemplo. Los datos incrustados de mujeres contienen observaciones sobre la estatura y el peso de 15 mujeres. Intentaremos entender la dependencia entre peso y estatura, gráficamente al principio (Figura\(\PageIndex{2}\)):

Código\(\PageIndex{1}\) (R):

women.lm <- lm(weight ~ height, data=women)
plot(weight ~ height, data=women, xlab="Height, in", ylab="Weight, lb")
grid()
abline(women.lm, col="red")
Cladd(women.lm, data=women) # asmisc.r
legend("bottomright", col=2:1, lty=1:2,
legend=c("linear relationship", "95% confidence bands"))

(Aquí usamos la función Cladd () que agrega bandas de confianza a la trama\(^{[1]}\).)

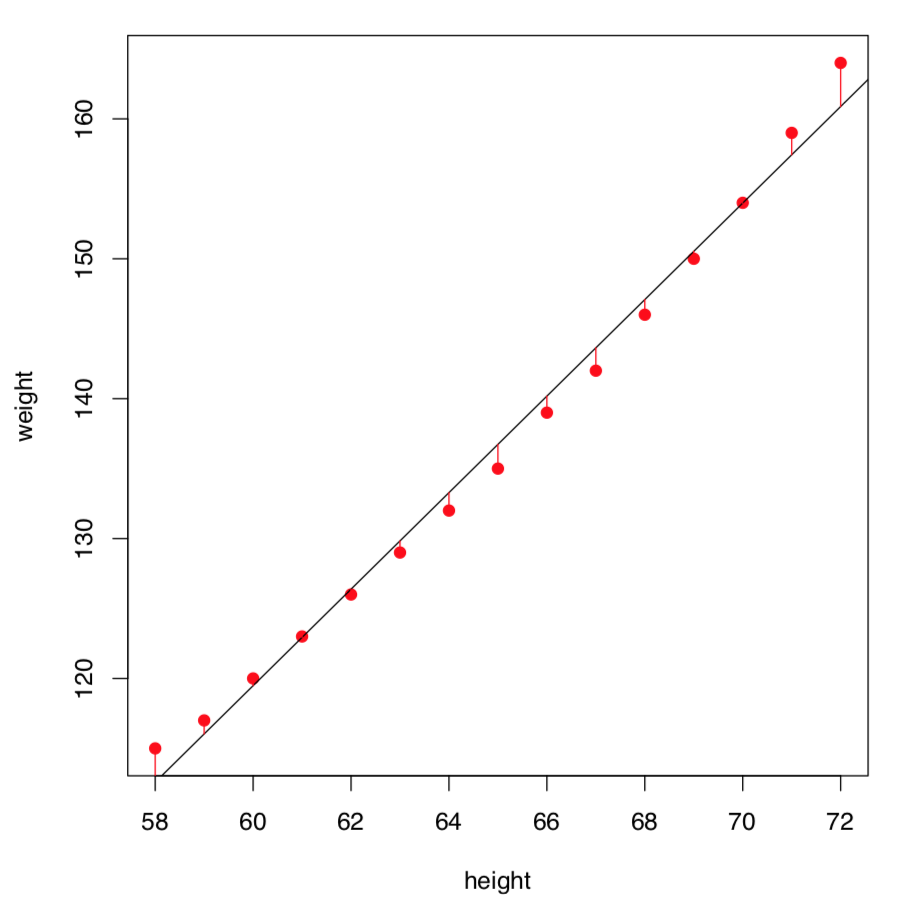
Visualicemos mejor los residuos (Figura\(\PageIndex{3}\)):

Código\(\PageIndex{2}\) (R):

women.lm <- lm(weight ~ height, data=women)
plot(weight ~ height, data=women, pch=19, col="red")
abline(women.lm)
with(women, segments(height, fitted(women.lm), height, weight, col="red"))

Para ver los resultados del análisis del modelo, podemos emplear summary ():

Figura\(\PageIndex{2}\) La relación entre altura y peso.

Código\(\PageIndex{3}\) (R):

women.lm <- lm(weight ~ height, data=women)
summary(women.lm)

Figura\(\PageIndex{3}\) Residuales del modelo lineal peso vs altura de las mujeres.

Esta salida larga es mejor para leer de abajo hacia arriba. Podemos decir que:

• La significancia de la relación (reflejada con R-cuadrado) es alta desde el punto de vista estadístico: F-estadística es\(1433\) con valor p global: 1.091e-14.
• El R-cuadrado (use Ajustado R-cuadrado porque esto es más adecuado para el modelo) es realmente grande,\(R^2 = 0.9903\). Esto significa que casi toda la variación en la variable de respuesta (peso) se explica por predictor (altura).

  R-cuadrado se relaciona con el coeficiente de correlación y podría ser utilizado como la medida del tamaño del efecto. Dado que es cuadrado, los valores altos comienzan desde 0.25:

Código\(\PageIndex{4}\) (R):

Mag(0.9903) # asmisc.r

• Ambos coeficientes son estadísticamente diferentes de cero, esto podría verse a través de “estrellas” (como ***), y también a través de los valores p reales Pr (>|t|): 1.71e-09 para la intercepción, y 1.09e-14 para la altura, que representa la pendiente.

  Para calcular la pendiente en grados, se podría ejecutar:

Código\(\PageIndex{5}\) (R):

women.lm <- lm(weight ~ height, data=women)
(atan(women.lm$coefficients[[2]]) * 180)/pi

• En general, nuestro modelo es:

Peso (estimado) = -87.51667 + 3.45 * Altura,

así que si la altura crece 4 pulgadas, el peso crecerá en aproximadamente 14 libras.

• El residuo positivo máximo es\(3.1167\) lb, el máximo negativo es\(-1.7333\) lb.
• La mitad de los residuos están bastante cerca de la mediana (dentro de aproximadamente\(\pm1\) el intervalo).

A primera vista, el resumen del modelo se ve bien. No obstante, antes de sacar conclusiones, también debemos verificar los supuestos del modelo. La trama de comando (women.lm) devuelve cuatro parcelas consecutivas:

• La primera gráfica, residuales vs. valores ajustados, es lo más importante. Idealmente, no debe mostrar estructura (variación uniforme y ninguna tendencia); esto satisface tanto los supuestos de linealidad como de homocedascicidad.
• Desafortunadamente, el modelo women.lm tiene una tendencia obvia que indica no linealidad. Los residuos son positivos cuando los valores ajustados son pequeños, negativos para los valores ajustados en el rango medio y positivos nuevamente para valores ajustados grandes. Claramente, se viola el primer supuesto del análisis de regresión lineal.

Código\(\PageIndex{6}\) (R):

oldpar <- par(mfrow=c(3, 3)) 
## Uniform variation and no trend:
for (i in 1:9) plot(1:50, rnorm(50), xlab="Fitted", ylab="Residuals")
title("'Good' Residuals vs. Fitted", outer=TRUE, line=-2) 
## Non-uniform variation plus trend:
for (i in 1:9) plot(1:50, ((1:50)*rnorm(50) + 50:1), xlab="Fitted",ylab="Residuals") 
title("'Bad' Residuals vs. Fitted", outer=TRUE, line=-2) 
par(oldpar) 

• Para entender mejor los residuos vs. parcelas ajustadas, por favor, ejecute el siguiente código usted mismo y busque en las parcelas resultantes:
• En la siguiente parcela, los residuos estandarizados no siguen perfectamente la línea normal (ver la explicación de la trama QQ en el capítulo anterior), pero son “lo suficientemente buenos”. Para revisar diferentes variantes de estas parcelas, ejecute usted mismo el siguiente código:

Código\(\PageIndex{7}\) (R):

oldpar <- par(mfrow=c(3, 3))
for (i in 1:9) { aa <- rnorm(50); qqnorm(aa, main=""); qqline(aa) }
title("'Good' normality QQ plots", outer=TRUE, line=-2) 
for (i in 1:9) { aa <- rnorm(50)^2; qqnorm(aa, main=""); qqline(aa) }
title("'Bad' normality QQ plots", outer=TRUE, line=-2) 
par(oldpar)

• Prueba para la normalidad también debería funcionar:

Código\(\PageIndex{8}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(women.lm$residuals) # asmisc.r

• La tercera, la gráfica Escala-Ubicación, es similar a los residuales vs. ajustados, pero en lugar de residuos “brutos” utiliza las raíces cuadradas de sus valores estandarizados. También se utiliza para revelar tendencias en las magnitudes de los residuos. En un buen modelo, estos valores deberían distribuirse más o menos aleatoriamente.
• Finalmente, la última gráfica demuestra qué valores ejercen mayor influencia sobre la forma final del modelo. Aquí los dos valores con más apalancamiento son la primera y la última mediciones, aquellas, de hecho, que se mantienen más alejadas de la linealidad.

(Si necesitas saber más sobre resumen y trazado de modelos lineales, consulta las páginas de ayuda con comandos? resumen.lm y? plot.lm. Por cierto, como ANOVA tiene muchas similitudes con el análisis del modelo lineal, en R se pueden ejecutar las mismas gráficas diagnósticas para cualquier modelo ANOVA.)

Ahora bien está claro que nuestro primer modelo lineal no funciona bien para nuestros datos que probablemente no sean lineales. Si bien existen muchos métodos de regresión no lineal, modificémoslo primero de una manera más sencilla para introducir la no linealidad. Una de las formas simples es agregar el término en cubos, porque el peso se relaciona con el volumen, y el volumen es un cubo de tamaños lineales:

Código\(\PageIndex{9}\) (R):

women.lm3 <- lm(weight ~ height + I(height^3), data=women)
summary(women.lm3)
plot(women.lm3, which=1) # just residuals vs. fitted

(La función I () se utilizó para decirle a R que la altura^3 es una operación aritmética y no la parte de la fórmula del modelo).

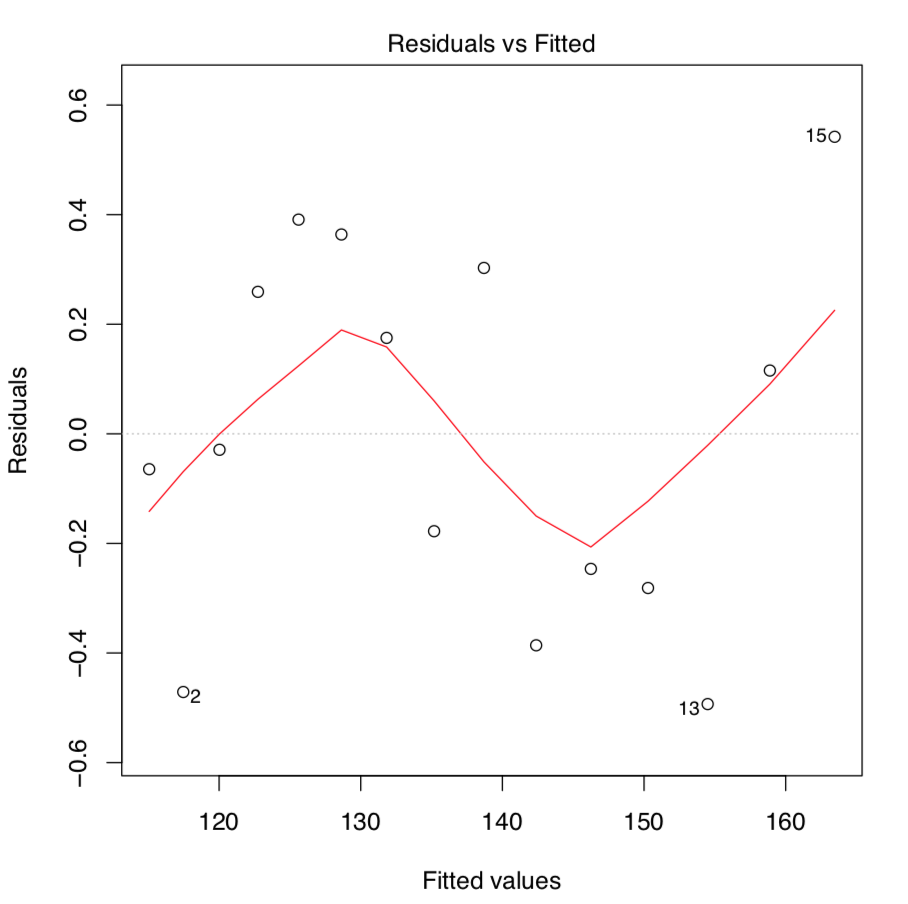
El rápido vistazo a los residuos vs. parcela ajustada (Figura\(\PageIndex{4}\)) muestra que este segundo modelo encaja mucho mejor! Las bandas de confianza y la línea predicha también se ven más apropiadas:

Figura\(\PageIndex{4}\) Residuales vs. parcela ajustada para el modelo de altura/peso femenino con el término cúbico.

Es posible que también desee ver los intervalos de confianza para los parámetros del modelo lineal. Para ello, use confint (mujeres.lm).

Otro ejemplo es de los datos de huevo estudiados gráficamente en el segundo capítulo (Figura 2.9.1). ¿La longitud del huevo se relaciona linealmente con con del huevo?

Código\(\PageIndex{10}\) (R):

eggs <- read.table("data/eggs.txt")
eggs.lm <- lm(V2 ~ V1, data=eggs)

Podemos analizar primero los supuestos:

Código\(\PageIndex{11}\) (R):

eggs <- read.table("data/eggs.txt")
eggs.lm <- lm(V2 ~ V1, data=eggs)
plot(eggs.lm)

Lo más importante, los residuos vs. ajustados no es perfecto pero podría considerarse como “lo suficientemente bueno” (por favor compruébalo tú mismo): no hay tendencia obvia, y los residuos parecen estar más o menos igualmente dispersos (se cumple la homocedasticidad). La distribución de los residuos es cercana a lo normal. Ahora podemos interpretar el resumen del modelo:

Código\(\PageIndex{12}\) (R):

eggs <- read.table("data/eggs.txt")
eggs.lm <- lm(V2 ~ V1, data=eggs)
summary(eggs.lm)

La significación de la pendiente significa que la línea está definitivamente inclinada (esto es en realidad lo que se llama “relación” en lenguaje común). Sin embargo, la intercepción no es significativamente diferente de cero:

Código\(\PageIndex{13}\) (R):

eggs <- read.table("data/eggs.txt")
eggs.lm <- lm(V2 ~ V1, data=eggs)
confint(eggs.lm)

(El intervalo de confianza para la intercepción incluye cero.)

Para verificar la magnitud del tamaño del efecto, se puede usar:

Código\(\PageIndex{14}\) (R):

eggs <- read.table("data/eggs.txt")
eggs.lm <- lm(V2 ~ V1, data=eggs)
Mag(summary(eggs.lm)$adj.r.squared)

Este es un efecto realmente grande.

El tercer ejemplo se basa en una idea sencilla para comprobar si el éxito en la prueba de opción múltiple depende del tiempo que se pase con ella. Los datos se presentan en el archivo exams.txt que contiene los resultados de dos pruebas de opción múltiple en una clase grande:

Código\(\PageIndex{15}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
str(ee)

La primera variable es el número de prueba, otras dos son orden de finalización del trabajo, y resultado número de puntos (de 50). Asumimos aquí que el pedido refleja el tiempo dedicado a la prueba. Seleccione uno de dos exámenes:

Código\(\PageIndex{16}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
ee3 <- ee[ee$EXAM.N == 3,]

... y trazar primero (por favor revise esta parcela usted mismo):

Código\(\PageIndex{17}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
ee3 <- ee[ee$EXAM.N == 3,]
plot(POINTS.50 ~ ORDER, data=ee3)

Bueno, no se produce ninguna relación visible. Ahora lo abordamos inferencialmente:

Código\(\PageIndex{18}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
ee3 <- ee[ee$EXAM.N == 3,]
ee3.lm <- lm(POINTS.50 ~ ORDER, data=ee3)
summary(ee3.lm)

Como es habitual, esta salida se lee de abajo hacia arriba. Primero, la significancia estadística de la relación está ausente, y la relación (R al cuadrado ajustado) en sí misma es casi cero. Incluso si la intercepción es significativa, la pendiente no lo es y por lo tanto fácilmente podría ser cero. No existe relación entre el tiempo empleado y el resultado de la prueba.

Para verificar dos veces si el enfoque del modelo lineal era aplicable en este caso, ejecute usted mismo las parcelas de diagnóstico:

Código\(\PageIndex{19}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
ee3 <- ee[ee$EXAM.N == 3,]
plot(ee3.lm)

Y como toque final, prueba la línea de regresión y las bandas de confianza:

Código\(\PageIndex{20}\) (R):

ee <- read.table("http://ashipunov.info/data/exams.txt", h=T)
ee3 <- ee[ee$EXAM.N == 3,]
abline(ee3.lm)
Cladd(ee3.lm, data=ee3)

Casi horizontal, sin relación. También es interesante comprobar si el otro examen fue de la misma manera. Por favor descúbrelo tú mismo.

). Por favor, encuentre qué caracteres de medición morfológicos están más correlacionados y verifique el modelo lineal de sus relaciones.

) planta. Por favor, encuentre qué par de caracteres morfológicos está más correlacionado y analice el modelo lineal que incluye estos caracteres. Además, verifique si la longitud de la hoja es diferente entre las tres mayores poblaciones de rocío solar.

Como los modelos lineales y ANOVA tienen muchos en común, no hay problema en el análisis de múltiples grupos con los métodos de regresión lineal predeterminados. Considere nuestros datos ANOVA:

Código\(\PageIndex{21}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
newcolor <- relevel(hwc$COLOR, "brown")
summary(lm(cbind(WEIGHT, HEIGHT) ~ newcolor, data=hwc))

Este ejemplo muestra pocos “trucos” adicionales. Primero, así es como analizar varias variables de respuesta a la vez. Esto es aplicable también a aov () — pruébalo tú mismo.

A continuación, muestra cómo re-nivelar factor poniendo primero uno de los niveles proximales. Eso ayuda a comparar coeficientes. En nuestro caso, demuestra que las rubias no difieren de los marrones en peso. Tenga en cuenta que las “intercepciones” aquí no tienen una relación clara con el trazado de relaciones lineales.

También es fácil calcular el tamaño del efecto porque R cuadrado es el tamaño del efecto.

Por último, pero no menos importante, por favor revise los supuestos del modelo lineal con parcela (lm (...)) . Por el momento en R, esto funciona sólo para respuesta singular.

¿Existe la relación lineal entre el peso y la talla en nuestros datos de ANOVA hwc?

Muchas líneas

En ocasiones, existe la necesidad de analizar no sólo las relaciones lineales entre variables, sino responder a la pregunta de segundo orden: comparar varias líneas de regresión.

En lenguaje de fórmulas, esto se describe como

respuesta ~ factor de influencia*

donde factor es una variable categórica responsable de la distinción entre líneas de regresión, y star (*) indica que estamos comprobando simultáneamente (1) respuesta de influencia (predictor), (2) respuesta de factor y (3) respuesta de interacción entre influencia y factor.

Este tipo de análisis se denomina frecuentemente ANCOVA, “ANÁLISIS DE COVARIACIÓN”. El ANCOVA verificará si existe alguna diferencia entre intercepción y pendiente de la primera línea de regresión e intercepciones y pendientes de todas las demás líneas de regresión donde cada línea corresponde con un nivel de factor.

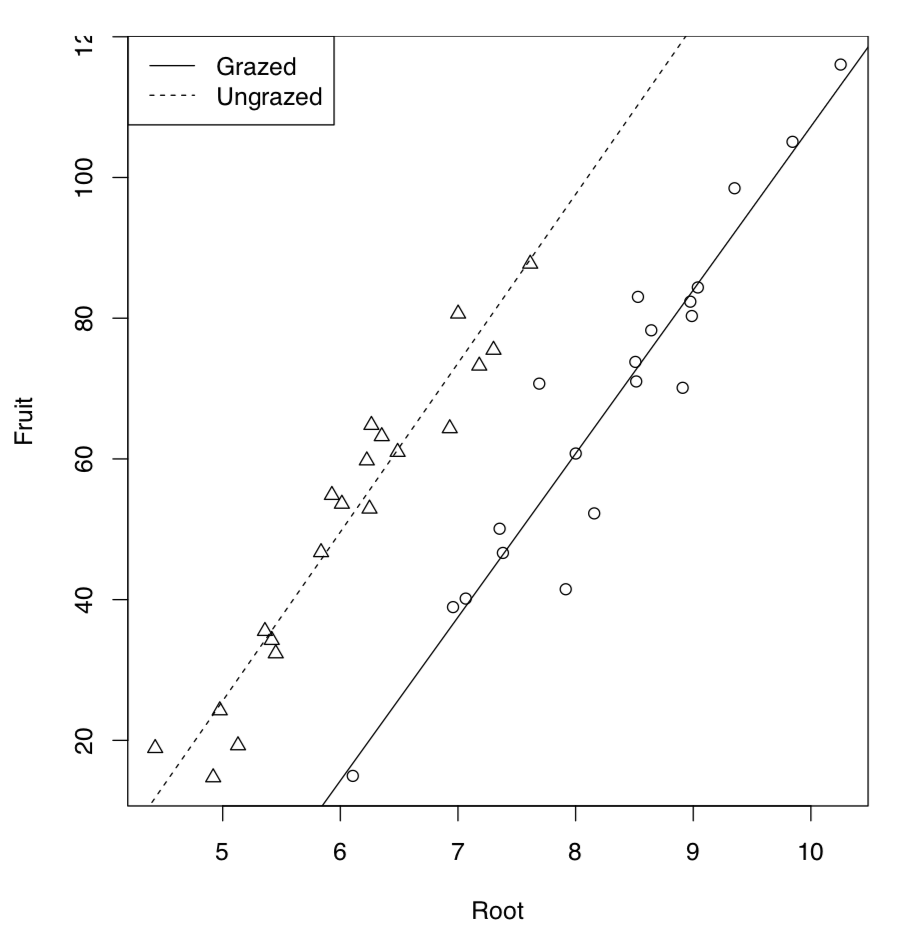
Partimos del ejemplo tomado del “R Book” de M.J. Crawley. 40 plantas fueron tratadas en dos grupos: pastoreadas (en las dos primeras semanas del cultivo) y no pastadas. También se midió el diámetro del portainjerto. Al final de la temporada se midió la producción de frutos secos de ambos grupos. Primero, analizamos los datos gráficamente:

Código\(\PageIndex{22}\) (R):

ipo <- read.table("data/ipomopsis.txt", h=TRUE)
with(ipo, plot(Root, Fruit, pch=as.numeric(Grazing)))
abline(lm(Fruit ~ Root, data=subset(ipo, Grazing=="Grazed")))
abline(lm(Fruit ~ Root, data=subset(ipo, Grazing=="Ungrazed")), lty=2)
legend("topleft", lty=1:2, legend=c("Grazed","Ungrazed"))

Como se observa en la parcela (Figura\(\PageIndex{5}\)), las líneas de regresión para plantas pastosas y no pastosas son probablemente diferentes. Ahora al modelo ANCOVA:

Figura Plantas\(\PageIndex{5}\) pastorizadas vs. no pastosas: modelos lineales.

Código\(\PageIndex{23}\) (R):

ipo <- read.table("data/ipomopsis.txt", h=TRUE)
ipo.lm <- lm(Fruit ~ Root * Grazing, data=ipo)
summary(ipo.lm)

La salida del modelo es similar al modelo lineal pero hay un término más presente. Este término indicó interacción que etiquetaba con colon. Dado que el factor de pastoreo tiene dos niveles ordenados alfabéticamente, el primer nivel (Pastado) se utiliza como predeterminado y por lo tanto (Intercept) pertenece al grupo de plantas pastadas. El intercepto del grupo no pastado se etiqueta como pastoreado. De hecho, esto ni siquiera es una intercepción sino diferencia entre intercepción de grupo no pastado e intercepción de grupo pastado. Análogamente, la pendiente para pastoreo se etiqueta como Raíz, y la diferencia entre las laderas de no pastado y pastado se etiqueta como Raíz:Pastoreado. Esta diferencia es la interacción, o cómo el pastoreo afecta la forma de relación entre el tamaño del portainjerto y el peso del fruto. Para convertir esta salida en fórmulas de regresión, se necesitarán algunos cálculos:

Fruto = -125.174 + 23.24 * Raíz (pastada) Fruto = (-125.174 + 30.806) + (23.24 + 0.756) * Raíz (no pastada)

Tenga en cuenta que la diferencia entre pendientes no es significativa. Por lo tanto, la interacción podría ser ignorada. Comprobemos si esto es cierto:

Código\(\PageIndex{24}\) (R):

ipo <- read.table("data/ipomopsis.txt", h=TRUE)
ipo.lm <- lm(Fruit ~ Root * Grazing, data=ipo)
ipo.lm2 <- update(ipo.lm, . ~ . - Root:Grazing)
summary(ipo.lm2)
AIC(ipo.lm)
AIC(ipo.lm2)

Primero, actualizamos nuestro primer modelo eliminando el término de interacción. Este es el modelo aditivo. Entonces summary () nos dijo que ahora todos los coeficientes son significativos (comprueba tú mismo su salida). Esto definitivamente es mejor. Finalmente, empleamos AIC (criterio de información de Akaike). La AIC vino de la teoría de la información y típicamente refleja la entropía, es decir, la adecuación del modelo. Cuanto más pequeño es AIC, mejor es un modelo. Entonces el segundo modelo es el inconfundible ganador.

Por cierto, podríamos especificar el mismo modelo aditivo usando signo más en lugar de estrella en la fórmula del modelo.

¿Qué dirá la AIC sobre nuestro ejemplo anterior, modelos de datos de mujeres?

Código\(\PageIndex{25}\) (R):

AIC(women.lm)
AIC(women.lm3)

Nuevamente, el segundo modelo (con el término en cubos) es mejor.

Es bien sabido que en el análisis de los resultados de las votaciones, la dependencia entre la asistencia y el número de personas votadas por el candidato en particular, juega un gran papel. Es posible, por ejemplo, dilucidar si se falsificaron las elecciones. Aquí utilizaremos el archivo de datos elections.txt que contiene los resultados de las votaciones de tres partidos rusos diferentes en más de 100 distritos:

Código\(\PageIndex{26}\) (R):

elections <- read.table("data/elections.txt", h=TRUE)
str(elections)

Para simplificar la mecanografía, adjuntaremos () el marco de datos (si haces lo mismo, no olvides separarlo () al final) y calcularemos proporciones de votantes y la asistencia general:

Código\(\PageIndex{27}\) (R):

elections <- read.table("data/elections.txt", h=TRUE)
attach(elections)
PROP <- cbind(CAND.1, CAND.2, CAND.3) / VOTER
ATTEN <- (VALID + INVALID) / VOTER

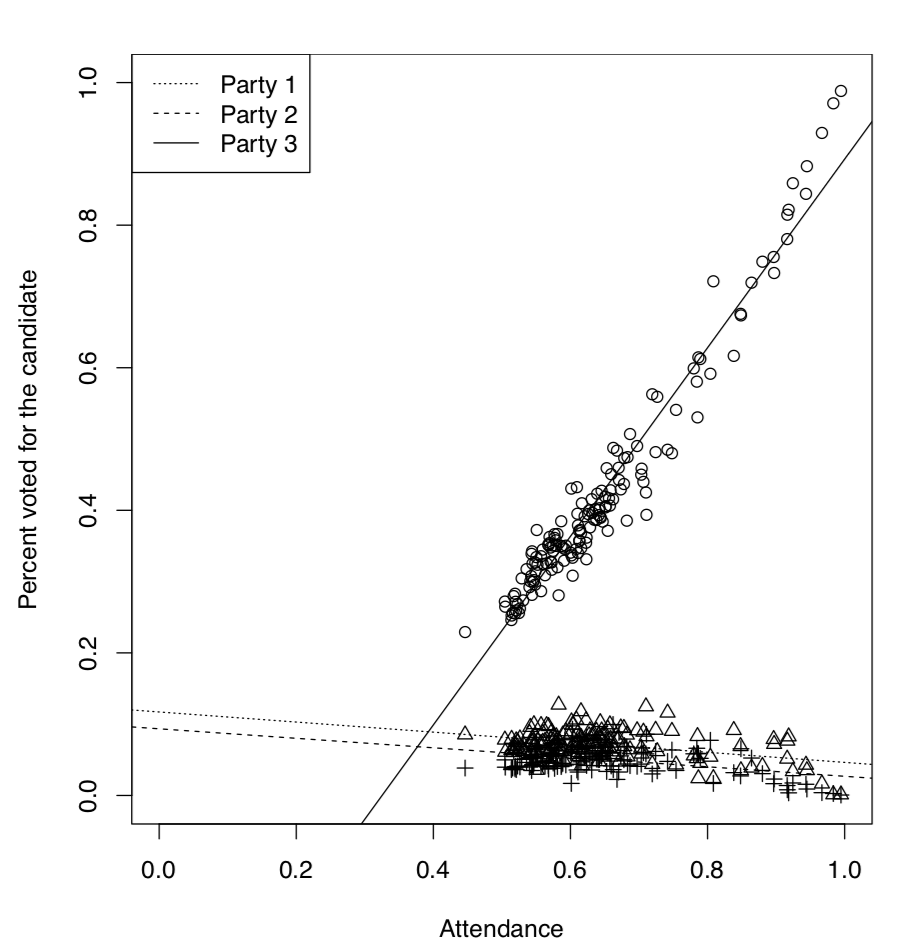
Ahora veremos gráficamente la dependencia entre asistencia y votación (Figura\(\PageIndex{6}\)):

Código\(\PageIndex{28}\) (R):

elections <- read.table("data/elections.txt", h=TRUE)
ATTEN <- (VALID + INVALID) / VOTER
lm.1 <- lm(CAND.1/VOTER ~ ATTEN)
lm.2 <- lm(CAND.2/VOTER ~ ATTEN)
lm.3 <- lm(CAND.3/VOTER ~ ATTEN)
plot(CAND.3/VOTER ~ ATTEN, xlim=c(0, 1), ylim=c(0, 1), xlab="Attendance", ylab="Percent voted for the candidate")
points(CAND.1/VOTER ~ ATTEN, pch=2)
points(CAND.2/VOTER ~ ATTEN, pch=3)
abline(lm.3)
abline(lm.2, lty=2)
abline(lm.1, lty=3)
legend("topleft", lty=c(3, 2, 1), legend=c("Party 1","Party 2","Party 3"))
detach(elections)

Por lo que el tercero tenía un proceso de votación que era sospechosamente diferente de los procesos de votación para otros dos partidos. Quedó claro incluso desde el análisis gráfico pero podríamos querer probarlo de manera inferencial, usando ANCOVA:

Código\(\PageIndex{29}\) (R):

elections <- read.table("data/elections.txt", h=TRUE)
PROP <- cbind(CAND.1, CAND.2, CAND.3) / VOTER
ATTEN <- (VALID + INVALID) / VOTER
elections2 <- cbind(ATTEN, stack(data.frame(PROP)))
names(elections2) <- c("atten","percn","cand")
str(elections2)

Figura Resultados de la\(\PageIndex{6}\) votación vs. asistencia para cada partido.

(Aquí creamos y verificamos el nuevo marco de datos. En elecciones2, todas las variables son ahora stack () 'ed en dos columnas, y la tercera columna contiene el código del partido.)

Código\(\PageIndex{30}\) (R):

elections <- read.table("data/elections.txt", h=TRUE)
PROP <- cbind(CAND.1, CAND.2, CAND.3) / VOTER
ATTEN <- (VALID + INVALID) / VOTER
elections2 <- cbind(ATTEN, stack(data.frame(PROP)))
ancova.v <- lm(percn ~ atten * cand, data=elections2)
summary(ancova.v)

Aquí (Intercept) pertenece específicamente al modelo para la primera fiesta. Su valor p indica si difiere significativamente de cero. El segundo coeficiente, atten, pertenece al predictor continuo, asistencia. No es una intercepción sino pendiente de una regresión. También se compara con cero.

Las siguientes cuatro filas representan diferencias con respecto a la primera parte, dos para intercepciones y dos para pendientes (esta es la forma tradicional de estructurar la salida en R). Los dos últimos ítems representan interacciones. Nos interesó más si existe una interacción entre la asistencia y la votación por el tercero, esta interacción es común en caso de falsificaciones y nuestros resultados apoyan esta idea.

(Figura\(\PageIndex{7}\), phenomenon when in each population there are mostly two types of plants: with flowers bearing long stamens and short style, and with flowers bearing long style and short stamens. It was proved that heterostyly helps in pollination. Please check if the linear dependencies between lengths of style and stamens are different in these two species. Find also which model is better, full (multiplicative, with interactions) or reduced (additive, without interactions).

Figura\(\PageIndex{7}\) Heterostyly en prímulas: flores de las diferentes plantas de una población.

Más de una manera, otra vez

Armados con el conocimiento sobre los modelos AIC, multiplicativos y aditivos, podemos regresar ahora a los diseños bidireccionales ANOVA, brevemente mencionados anteriormente. Considera el siguiente ejemplo:

Código\(\PageIndex{31}\) (R):

ToothGrowth.1 <- with(ToothGrowth, data.frame(len, supp, fdose=factor(dose)))
str(ToothGrowth.1)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(ToothGrowth$len)
with(ToothGrowth, fligner.test(split(len, list(dose, supp))))

(Para comenzar, convertimos la dosis en factor. De lo contrario, nuestro modelo será ANCOVA en lugar de ANOVA.)

Supuestos cumplidos, ahora el análisis central:

Código\(\PageIndex{32}\) (R):

ToothGrowth.1 <- with(ToothGrowth, data.frame(len, supp, fdose=factor(dose)))
summary(aov(len ~ supp * fdose, data=ToothGrowth.1))
summary(aov(len ~ supp + fdose, data=ToothGrowth.1))
AIC(aov(len ~ supp + fdose, data=ToothGrowth.1))

Ahora vemos lo que ya era visible en la gráfica de interacción (Figura 5.3.4: modelo con interacciones es mejor, y significativo son los tres términos: dosis, suplemento e interacción entre ellos.

El tamaño del efecto es muy alto:

Código\(\PageIndex{33}\) (R):

ToothGrowth.1 <- with(ToothGrowth, data.frame(len, supp, fdose=factor(dose)))
Eta2 <- function(aov){summary.lm(aov)$r.squared}
Eta2(aov(len ~ supp * fdose, data=ToothGrowth.1))

Las pruebas post hoc suelen ser más peligrosas en el análisis bidireccional, simplemente porque hay muchas más comparaciones. Sin embargo, es posible ejecutar TukeyHSD ():

Código\(\PageIndex{34}\) (R):

ToothGrowth.1 <- with(ToothGrowth, data.frame(len, supp, fdose=factor(dose)))
TukeyHSD(aov(len ~ supp * fdose, data=ToothGrowth.1))

Aquí se omite el resto de comparaciones, pero TukeyHSD () tiene un método de trazado que permite trazar el elemento único o último (Figura 6.3.1):

Código\(\PageIndex{35}\) (R):

ToothGrowth.1 <- with(ToothGrowth, data.frame(len, supp, fdose=factor(dose)))
TukeyHSD(aov(len ~ supp * fdose, data=ToothGrowth.1))
plot(TukeyHSD(aov(len ~ supp * fdose, data=ToothGrowth.1)), las=1)

Referencias

1. La función Cladd () es aplicable solo a modelos lineales simples. Si quieres bandas de confianza en casos más complejos, comprueba el código Cladd () para ver qué hace exactamente.