3: Examen de la evidencia mediante gráficos y estadísticas
- Page ID
- 150435
Vivimos en un mundo en el que las decisiones deben tomarse sin información completa. Sabiendo esto, buscamos intuitivamente recopilar la mayor cantidad de información posible antes de tomar la decisión real. Considera el matrimonio, que es una decisión bastante importante. Nunca podremos saber todo lo posible sobre una persona con la que nos gustaría casarnos pero sí buscamos la mayor cantidad de información posible saliendo primero. El empleo es otro ejemplo de decisión importante, tanto para el empleador como para el empleado potencial. En cada caso, la información se obtiene a través de entrevistas, currículums, referencias e investigaciones antes de dar o aceptar una oferta de trabajo.
Ante una decisión que se basará en datos, es la producción de gráficas y estadísticas que serán análogas a las citas y entrevistas. Los datos que se recojan deben ser útiles para responder a las preguntas que se formularon. El capítulo 2 se centró tanto en la planeación del experimento como en el proceso de selección aleatoria que es importante para producir buenos datos de muestra. El capítulo 3 ahora se centrará en qué hacer con los datos una vez que los tenga.
Tipos de datos
Ya hemos clasificado los datos en dos categorías. Los datos numéricos se consideran cuantitativos mientras que los datos que consisten en palabras se denominan datos categóricos o cualitativos. Los datos cuantitativos se pueden subdividir en datos discretos y continuos.
- Los datos discretos contienen un número finito de valores posibles porque a menudo se basan en recuentos. A menudo estos valores son números enteros, pero eso no es un requisito. Ejemplos de datos discretos incluyen el número de salmones que migran por un arroyo para desovar, el número de vehículos que cruzan un puente cada día o el número de personas sin hogar en una comunidad.
- Los datos continuos contienen un número infinito de valores posibles porque a menudo se basan en mediciones, que en teoría podrían medirse a muchos decimales si la tecnología existiera para hacerlo. Ejemplos de datos continuos incluyen el peso del salmón que está desovando, el tiempo que lleva cruzar el puente, o la cantidad de calorías que consume una persona sin hogar en un día.
Los datos cuantitativos discretos y los datos categóricos a menudo se confunden. Observe los datos reales que se escribirían para cada unidad de la muestra para determinar el tipo de datos. Como ejemplo, considere el escarabajo marrón, que está infectando árboles en el oeste de Estados Unidos y Canadá. Si el propósito de la investigación era determinar la proporción de árboles que están infectados, entonces los datos que se recolectarían para cada árbol son “infectados” o “no infectados”. En definitiva, el investigador contaría el número de árboles marcados infectados o no infectados, pero los datos en sí serían esas palabras. Si el propósito de la investigación fue determinar el número promedio de escarabajos pardos en cada árbol, entonces los datos que se recopilarían son “el número de escarabajos pardos en un árbol”, que es un recuento. Así, los recuentos están involucrados tanto para datos cuantitativos categóricos como discretos. Los datos categóricos se cuentan como si los datos categóricos se contaran en múltiples lugares o tiempos, luego los recuentos se convierten en datos cuantitativos discretos. Por ejemplo, en la clase de hoy, los alumnos de la lista de clase pueden marcarse como presentes o ausentes y esto sería categórico. No obstante, si consideramos el número de alumnos que han estado presentes en cada clase durante la semana pasada, entonces los datos en los que nos interesa son discretos cuantitativos.
Examinar la evidencia de los datos de la muestra
Dado que los datos de muestra son nuestra ventana hacia los datos estocásticos en la población, necesitamos formas de hacer que los datos sean significativos y comprensibles. Esto se logra mediante el uso de una combinación de gráficos y estadísticas. Hay una o más gráficas y estadísticas que son apropiadas para cada tipo de datos. En las siguientes secciones aprenderás a hacer las gráficas a mano y a encontrar las estadísticas. Hay muchas otras gráficas que existen además de esta colección, pero estas son las básicas.
Examinar la evidencia proporcionada por los datos categóricos de la muestra
Hay dos gráficas y dos estadísticas que son apropiadas para los datos categóricos. Los gráficos más utilizados son los gráficos de barras y los gráficos circulares. Las estadísticas son conteos y proporciones. Si la hipótesis que se está probando es sobre recuentos, entonces se debe usar un gráfico de barras y recuentos de muestras. Si la hipótesis que se está probando es sobre proporciones, entonces se debe usar un gráfico circular y proporciones de muestra. Para los datos categóricos, las estadísticas se encuentran primero y luego se utilizan en la producción de una gráfica.
Recuentos y gráficos de barras
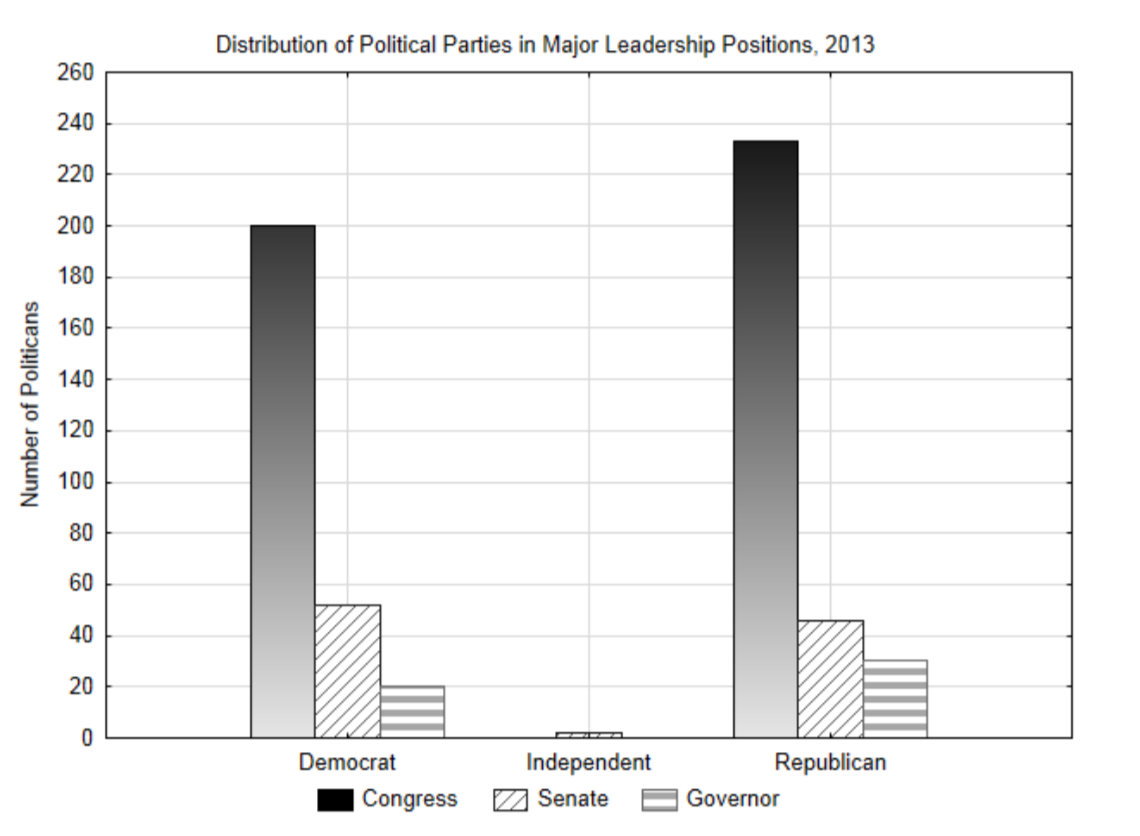
El liderazgo político en EU suele dividirse entre dos partidos políticos, los demócratas y los republicanos. Sólo unos pocos políticos han sido elegidos como independientes, lo que significa que no pertenecen a uno de estos partidos. Los cargos más altos de elección política distintos del Presidente son congresistas, senadores y gobernadores estatales. Si queremos entender la distribución de los partidos políticos en 2013, entonces el partido político de nuestros dirigentes es un dato categórico que se puede poner en una tabla de contingencia en la que cada célula representa un recuento del número de personas que encajan tanto en la categoría de posición de liderazgo como en la categoría de partido político. Se puede hacer un gráfico de barras a partir de estos recuentos.
| 2013 | Posición de liderazgo | |||
| Congreso | Senado | Gobernador | ||
| Partido Político | Demócratas | 200 | 52 | 20 |
| Independientes | 0 | 2 | 0 | |
| Republicanos | 233 | 46 | 30 | |
Proporciones y gráficos circulares
Las encuestas de opinión suelen utilizar proporciones o porcentajes para mostrar apoyo a candidatos o iniciativas. La diferencia entre proporciones y porcentajes es que los porcentajes se obtienen multiplicando la proporción por 100. Así, una proporción de 0.25 equivaldría a 25%. Las fórmulas utilizan proporciones mientras que a menudo nos comunicamos verbalmente usando porcentajes. Deberías poder moverte de uno a otro sin esfuerzo.
Casi siempre hay dos proporciones de interés para nosotros. La proporción poblacional, representada con el símbolo p, es la proporción que realmente nos gustaría saber, pero que suele ser incognoscible. Hacemos hipótesis sobre p. La proporción muestral, representada con\(\hat{p}\), es lo que podemos encontrar a partir de los datos de la muestra y se utiliza para probar la hipótesis. La fórmula para las proporciones son:
\[p = \dfrac{x}{N}\]
y
\[\hat{p} = \dfrac{x}{n}\]
donde\(x\) es un recuento del número de valores en una categoría,\(N\) es el tamaño de la población, y\(n\) es el tamaño de la muestra.
Los resultados de dos encuestas discutidas en un blog washingtonstatewire.com serán utilizados para un ejemplo. Dado que gran parte del bloqueo del transporte es causado por los autos, y que los puentes del estado de Washington necesitan mantenimiento (hubo un colapso de puente en la Interestatal 5 cerca de Mount Vernon, WA en 2013), sería natural preguntarse sobre el apoyo de los votantes para el financiamiento estatal de proyectos de transporte. Se realizaron dos encuestas aproximadamente a la misma hora del 2013. (washingtonstatewire.com/blog/... portación-impuesto-paquete-ofrece-una-medida-de-mood-votante-después-puente-colapso/ visto 7-25-13.)
La encuesta 1 utilizó entrevistadores humanos que comenzaron una entrevista con guión al observar que “por supuesto los proyectos de transporte son caros y tardan mucho en completarse”, y concluyó con, “como dije, los proyectos de transporte son caros. La otra parte del paquete será cómo pagar esas mejoras. A nadie le gusta subir impuestos, pero mientras leo algunas opciones de financiamiento, dígame si favorecería la propuesta, se inclinaría a aceptarla, se inclinaría a oponerse, o la encontraría inaceptable”.
La encuesta 2 utilizó el sondeo automático que preguntaba a los votantes si es importante que “la legislatura apruebe un paquete estatal este año para abordar los problemas de congestión y seguridad, financiar el mantenimiento y mejora de carreteras y puentes, y proporcionar fondos adicionales para el tránsito”.
Lo mejor que se puede estimar a partir del artículo, los resultados de la Encuesta 1 fueron que 160 de las 400 personas encuestadas apoyaron el aumento de impuestos para mejorar el sistema de transporte. Los resultados de la Encuesta 2 fueron que 414 de 600 piensan que es importante que la Legislatura apruebe el paquete de financiamiento.
A partir de datos como este podemos hacer un gráfico circular. Esto se demostrará con Poll 1 y luego deberías hacer un gráfico circular para Poll 2.
El primer paso para hacer un gráfico circular es calcular la proporción de valores en cada grupo. En la Encuesta 1, consideraremos que hay dos grupos. El primer grupo es para quienes apoyaron el aumento de impuestos y el segundo grupo es para los que no apoyaron el aumento de impuestos. Dado que 160 de cada 400 personas apoyaron el aumento de impuestos, entonces la proporción se encuentra dividiendo 160 por 400. Por lo tanto,\(\hat{p} = \dfrac{160}{400} = 0.40\). Como
recordatorio,\(\hat{p}\) es la proporción de la muestra que apoya el aumento de impuestos. Se trata de una estadística, que proporciona una visión de la proporción poblacional, representada con la variable p. A los legisladores les gustaría saber el valor de p, pero eso requeriría hacer un censo, por lo que deben conformarse con la proporción muestral,\(\hat{p}\). Es probable que la p no sea igual\(\hat{p}\), sino que esté cerca de ese valor. Al hacer un gráfico circular, dibuja la línea que separa las rebanadas para que el 40% del círculo esté en una rebanada, lo que significa que el 60% del círculo está en la otra.
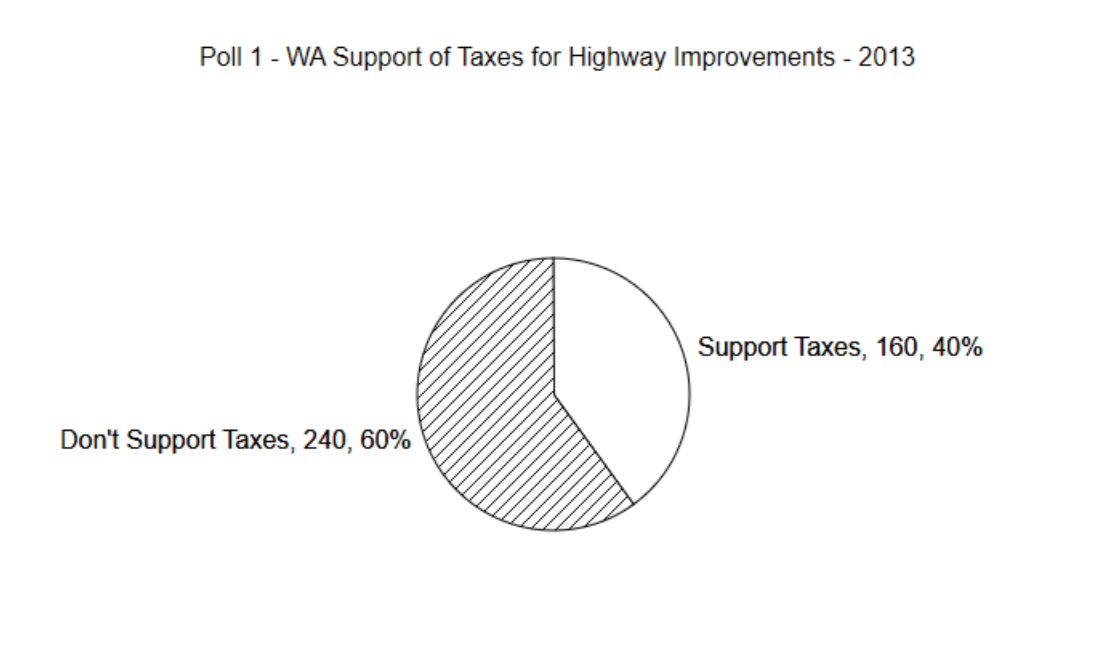
Hay algunas cosas que notar sobre el gráfico circular. Primero, contiene un título que describe el contenido de la gráfica. A continuación, cada segmento contiene una etiqueta que explica brevemente el significado del segmento, el número de valores de datos que contribuyeron al segmento y el porcentaje de todos los valores que se ponen en el segmento. ¿Por qué debería incluirse toda esta información?
Si vas a utilizar alguna gráfica para mostrar los resultados de tu investigación, es importante comunicar esos resultados con claridad. El objetivo es producir gráficas fáciles de leer. Un lector que mire una gráfica sin etiquetar no podrá obtener ninguna comprensión de ella, y así no has podido comunicar algo importante. Se incluye el porcentaje para facilitar al lector conocer el porcentaje de valores en cada rebanada. Sin los porcentajes, una persona tendría que adivinar el porcentaje y es probable que su conjetura no sea precisa. Incluir el número de personas en cada porción es importante porque le da al lector una indicación de cuán seriamente tratar los resultados. Una encuesta a 40 personas de las cuales 16 impuestos soportados tendrían un gráfico circular idéntico al anterior. De igual manera, una encuesta a 40 mil personas, de las cuales 16 mil apoyaban impuestos, también sería idéntica a la gráfica anterior. Cuanta más gente haya, más fuerte será el apoyo. Esto debería ser obvio a partir de la gráfica y por lo tanto es importante incluir el valor.
Hay que mencionar los gráficos por computadora ya que la mayoría de los gráficos circulares se producen en una computadora. Si bien las computadoras pueden hacer gráficos muy elegantes y coloridos, los colores pueden ser indistinguibles si se imprimen en una impresora en blanco y negro o foto copiada en blanco y negro. Ten esto en cuenta cuando hagas gráficas y escojas colores que serán distinguibles cuando se copien en blanco y negro.
Utilice los resultados de Sondeo 2 para producir un gráfico circular completamente etiquetado. Encuentra primero la proporción muestral.
¿Estas dos encuestas producen resultados similares u resultados opuestos? ¿Las preguntas estaban bien redactadas?
¿Por qué o por qué no?
Se necesita hacer una última palabra sobre los gráficos circulares. En algunos círculos, los gráficos circulares no se consideran gráficos útiles. Hay alguna evidencia de que la gente no hace un buen trabajo interpretándolos. Los gráficos circulares rara vez aparecen en las revistas académicas. Sin embargo, los gráficos circulares aparecen en medios impresos y pueden dar una indicación de cómo se divide el conjunto. Pueden ser de beneficio para quienes gustan de la representación visual, en lugar de solo las estadísticas.
Examinar la evidencia proporcionada por los datos cuantitativos de la muestra
Los tres tipos más comunes de gráficos utilizados para los datos cuantitativos son los histogramas, las gráficas de caja y las gráficas de dispersión. Los histogramas y diagramas de caja se utilizan para los datos univariados, mientras que los gráficos de dispersión se utilizan para los datos bivariados. Una variable es una única medida u observación de una variable aleatoria obtenida para cada sujeto o unidad en una muestra. (Sokal, Robert R. y F. James Rohlf. Introducción a la Bioestadística. Nueva York: Freeman, 1987, Imprimir.) Cuando sólo hay una variable aleatoria que se está considerando, los datos que se recogen son univariados. Cuando se están considerando simultáneamente dos variables aleatorias para la misma unidad, entonces los datos de las dos variables se consideran bivariados. Ejemplos de datos univariados incluyen el número de vehículos en un tramo de carretera, la cantidad que cuesta para que un estudiante obtenga su título o la cantidad de agua que usa un hogar cada mes. Ejemplos de datos bivariados incluyen el emparejamiento del número de autos en la carretera y el tiempo de viaje, la cantidad de matrícula y la cantidad de ayuda económica que usa un estudiante, o el número de personas en un hogar y la cantidad de agua utilizada.
Las estadísticas utilizadas para los datos univariados se ajustan a uno de los dos objetivos. El primer objetivo es definir el centro de los datos y el segundo objetivo es definir la variación que existe en los datos. Las formas más comunes de definir el centro son con la media aritmética y la mediana, aunque estas no son las únicas dos medidas de centro. En los casos en que se utiliza la media aritmética, la variación se cuantifica mediante desviación estándar. El estadístico más utilizado para los datos bivariados es la correlación, que indica la fuerza de la relación lineal entre las dos variables.
Histogramas
Los capítulos uno y dos contenían numerosos ejemplos de histogramas. Se utilizan para mostrar la distribución de los datos mostrando la frecuencia o conteo de datos en cada clase. El proceso de creación de histogramas a mano incluye los siguientes pasos.
- Identificar los valores de datos más bajos y altos.
- Cree límites fáciles de leer que se utilizarán para ordenar los datos en 4 a 10 clases. El límite más bajo debe ser un número que sea igual, o es un buen número por debajo, el valor de datos más bajo. El ancho de clase, que es la diferencia entre límites consecutivos, debe ser un factor de los valores de límite.
- Hacer una distribución de frecuencia para proporcionar una estructura organizada para contar el número de valores de datos en cada clase.
- Cree el histograma etiquetando el eje x con los límites inferiores y el eje y con las frecuencias. La altura de las barras refleja el número de valores en cada clase. Las barras adyacentes deben tocarse.
- Poner un título en la gráfica y en cada eje.
No hay una manera matemática precisa de elegir el valor inicial y el ancho de clase para un histograma. Más bien, es necesario pensar algo para usar números que sean fáciles de entender para un lector. Por ejemplo, si el número más bajo en un conjunto de datos es 9 y el número más alto es 62, entonces usar un valor inicial de 0 y un ancho de clase de 10 resultaría en la creación de 7 clases con límites fáciles de leer de 0,10,20,30,40,50,60, y 70. Por otro lado, a partir de 9 y usar un ancho de clase de 10 no se producirían límites fáciles de leer (9,19,29,...). Números como 2,4,6,8... o 5,10,15,20... o cualquier versión de estos números si se multiplican por una potencia de 10 hacen buenos límites de clase.
Una vez que se han determinado los límites de clase, se crea una distribución de frecuencia. Una distribución de frecuencia es una tabla que muestra las clases y proporciona un lugar para contar el número de valores de datos en cada clase. La distribución de frecuencias también debería ayudar a aclarar a qué clase se le darán los valores límite. Por ejemplo, ¿se pondría un valor de 20 en una clase 10 — 20 o una clase 20 — 30? Si bien no existe un acuerdo universal sobre este tema, parece un poco más lógico que se agrupen todos los valores que comienzan con un mismo número. Así, 20 se pondrían en la clase 20 — 30 que contiene todos los valores desde 20.000 hasta 29.999. Esto se puede mostrar de algunas maneras como se demuestra en la siguiente tabla.
| 0 hasta, pero sin incluir 10 | \(0 \le x < 10\) | [0, 10) |
| 10 hasta, pero sin incluir 10 | \(10 \le x < 20\) | [10, 20) |
| 20 hasta, pero sin incluir 10 | \(20 \le x < 30\) | [20, 30) |
| 30 hasta, pero sin incluir 10 | \(30 \le x < 40\) | [30, 40) |
Las tres columnas indican las mismas clases. La tercera columna utiliza notación de intervalos y debido a que es explícita y utiliza la menor cantidad de escritura, será el método utilizado en este texto. Como recordatorio sobre la notación de intervalos, el símbolo “[“indica que se incluye el número bajo mientras que el símbolo “) “indica que el número alto no está incluido.
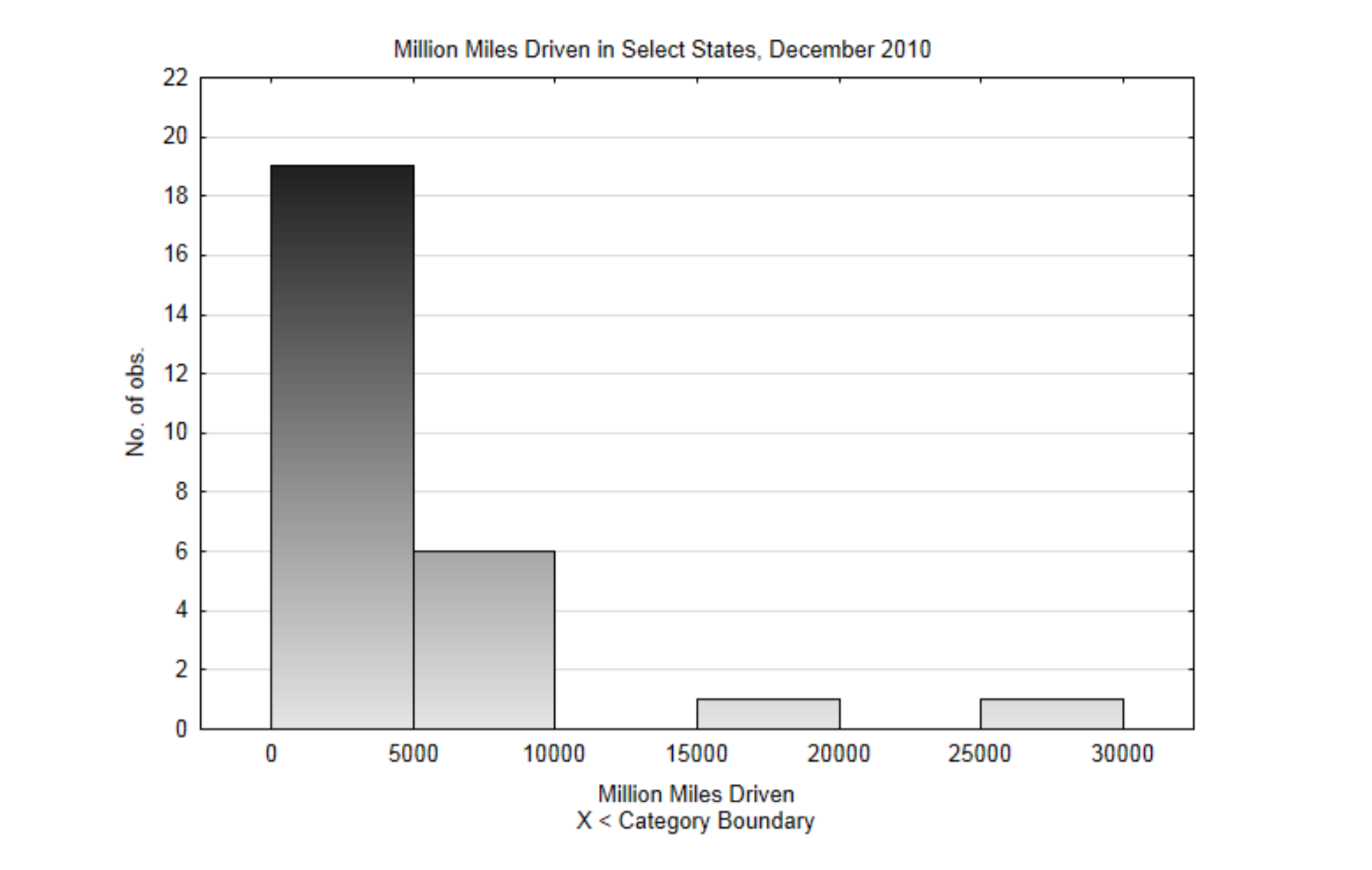
Para demostrar la construcción de un histograma, se utilizarán datos del Departamento de Transporte de Estados Unidos, Administración Federal de Carreteras. (Explore.data.gov/transportat... 3-mssz,7-28-13) El dato es el número estimado de millas recorridas en un estado en diciembre de 2010. Se utilizará una muestra estratificada ya que los datos ya están divididos en regiones del país. Los datos de la tabla tienen unidades de millones de millas.
| 4778 | 768 | 859 | 3816 |
| 6305 | 4425 | 789 | 1517 |
| 9389 | 3681 | 21264 | 8394 |
| 583 | 2958 | 2034 | 2362 |
| 712 | 5858 | 738 | 7861 |
| 5664 | 352 | 16256 | 2594 |
| 665 | 28695 | 4435 |
- El valor bajo es 352, el valor alto es 28,695.
- El límite de clase más bajo será 0, el ancho de clase será 5000. Esto producirá 6 clases.
- Esta es la distribución de frecuencias que incluye un recuento del número de valores en cada clase.
| Clases | Frecuencia |
|---|---|
| [0, 5000) | 19 |
| [5000, 10000) | 6 |
| [10000, 15000) | 0 |
| [15000, 20000) | 1 |
| [20000, 25000) | 0 |
| [25000, 30000) | 1 |
4, Este es el histograma completamente etiquetado. Observe cómo la altura de las barras corresponde con las frecuencias en la distribución de frecuencias.
Supongamos que queremos comparar la cantidad de manejo en estados con un área grande con aquellos con un área más pequeña. Esto podría hacerse usando un histograma de barras múltiples en el que un conjunto de barras será para estados más grandes y el otro para estados más pequeños.
Distribución de frecuencia e histograma de barras múltiples:
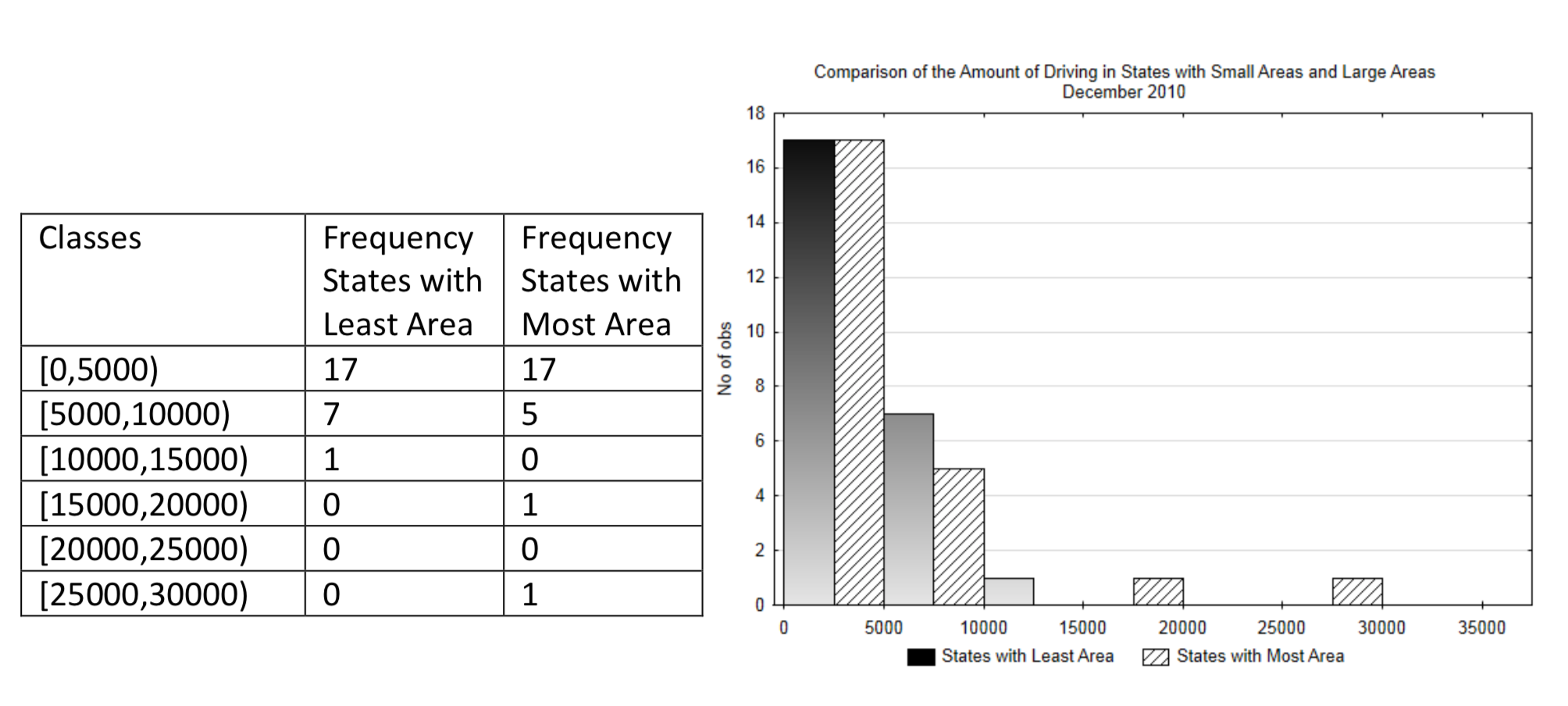
Interpretación: Si bien podría ser razonable suponer que habría más conducción en estados más grandes porque la distancia entre ciudades es mayor, es difícil discernir a partir de esta gráfica si ese es el caso. Por lo tanto, además del uso de una gráfica, estos datos se pueden comparar utilizando la media aritmética y la desviación estándar.
Media Aritmética, Varianza y Desviación Estándar
La media aritmética y la desviación estándar son estadísticas comunes utilizadas en conjunto con histogramas. La media es probablemente la forma más utilizada para identificar el centro de datos, pero no es el único método. La media se puede considerar como el punto de equilibrio para los datos, al igual que el punto de apoyo en un tambaleo. Los valores alejados de la media tienen un mayor impacto en ella que los valores más cercanos a la media de la misma manera que un niño pequeño sentado al final de un tambaleo puede equilibrarse con una persona más grande sentada cerca del fulcro.
Casi siempre hay dos medios aritméticos de interés para nosotros. La media poblacional, representada con el símbolo\(\mu\) (mu), es la media que realmente nos gustaría saber, pero que suele ser incognoscible. Hacemos hipótesis sobre\(\mu\). La media muestral, representada con\(\bar{x}\) (x-bar), es lo que podemos encontrar de una muestra y es lo que se utiliza para probar la hipótesis. La fórmula para las medias, como se muestra en el Capítulo 1, son:
\(\mu = \dfrac{\sum x_i}{N}\)y\(\bar{x} = \dfrac{\sum x_i}{n}\)
Donde\(\sum\) se usa una sigma mayúscula en notación de suma que significa sumar todo lo que sigue, x i es el conjunto de valores de datos y N es el número de valores en la población y n es el número de valores en la muestra. Estas fórmulas dicen sumar todos los valores y dividir por el número de valores.
Hay varias razones por las que la media aritmética se usa comúnmente y algunas razones por las que no se debe usar a veces. Una razón principal por la que se usa comúnmente es porque la media muestral es un estimador imparcial de la media poblacional. Esto se debe a que cerca de la mitad de los medios muestrales que podrían obtenerse de una población serán menores que la media poblacional y la mitad será mayor. Una media aritmética no es la mejor medida de centro cuando hay algunos valores extremadamente altos en los datos, ya que tendrán más impacto en la media que en los valores restantes.
Además de la media, también es útil saber cuánta variación existe en los datos. Observe en el histograma de doble barra cómo los datos en los estados con el área más grande se extienden más que los datos en los estados con el área más pequeña. Cuanto más dispersos están los datos, más difícil es obtener un resultado significativo a la hora de probar hipótesis.
La desviación estándar es la forma primaria en la que se cuantifica la dispersión de los datos. Se puede considerar como la distancia promedio aproximada entre cada valor de datos y la media. Al igual que con la media, hay dos valores de desviación estándar que nos interesan. La desviación estándar poblacional, representada con el símbolo σ (sigma minúscula), es la desviación estándar que realmente nos gustaría saber, pero que suele ser incognoscible. La desviación estándar de la muestra, representada con s, es lo que podemos encontrar de una muestra. Las fórmulas de desviación estándar son:
\[\sigma = \sqrt{\dfrac{\sum (x - \mu)^2}{N}}\]
y
\[s = \sqrt{\dfrac{\sum (x - \bar{x})^2}{n - 1}}\]
Los datos de huracanes en el Atlántico Norte se utilizarán para demostrar el proceso de búsqueda de la media y desviación estándar. (Datos de: www.wunderground.com/hurrican... asp? region=ep.)
| Año | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Número de huracanes | 15 | 5 | 6 | 8 | 3 | 12 | 7 |
Dado que se trata de una muestra, la fórmula apropiada para encontrar la media de la muestra es\(\bar{x} = \dfrac{\sum x_i}{n}\). El cálculo es\(\dfrac{15 + 5 + 6 + 8 + 3 + 12 + 7}{7} = \dfrac{56}{7} = 8\). Hubo un promedio de 8 huracanes en el Atlántico Norte por año entre 2005 y 2011. Observe que no hubo 8 huracanes cada año. Esto se debe a que hay variación natural en el número de huracanes. Podemos usar la desviación estándar como una forma de determinar la cantidad de variación. Para ello, construiremos una tabla de 3 columnas para ayudar con los cálculos.
| x | \((x - \bar{x})\) | \((x - \bar{x})^2\) |
|---|---|---|
| 15 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">15- 8 = 7 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((7)^2 = 49\) |
| 5 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">5 - 8 = -3 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((-3)^2 = 9\) |
| 6 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">6 - 8 = -2 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((-2)^2 = 4\) |
| 8 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">8 - 8 = 0 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((0)^2 = 0\) |
| 3 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">3 - 8 = -5 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((-5)^2 = 25\) |
| 12 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">12 - 8 = 4 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((4)^2 = 16\) |
| 7 | \ ((x -\ bar {x})\)” style="vertical-align:middle; ">7 - 8 = -1 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\((-1)^2 = 1\) |
| \ ((x -\ bar {x})\)” style="vertical-align:middle; ">\(\sum (x - \bar{x}) = 0\) | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">\(\sum (x - \bar{x})^2 = 0\) |
Dado que se trata de una muestra, la fórmula apropiada para encontrar la desviación estándar de la muestra es la\(s = \sqrt{\dfrac{\sum (x - \bar{x})^2}{n - 1}}\) que, después de la sustitución es\(\sqrt{\dfrac{104}{7 - 1}} = 4.16\). Este número indica que la variación promedio con respecto a la media en cada año es de 4.16 huracanes.
La varianza es otra medida de variación que está relacionada con la desviación estándar. La varianza es el cuadrado de la desviación estándar o, por el contrario, la desviación estándar es la raíz cuadrada de la varianza. Las fórmulas para varianza son:
\[\sigma ^2 = \dfrac{\sum (x - \mu)^2}{N}\]
y
\[s^2 = \dfrac{\sum (x - \bar{x})^2}{n - 1}\]
En el ejemplo sobre huracanes, la varianza es\(s^2 = \dfrac{104}{7 - 1} = 17.33\).
Medianas y parcelas de caja
Otra combinación de estadísticas y gráficas son las medianas y las gráficas de caja. Se encuentra una mediana antes de que se pueda crear una gráfica de caja. Una mediana es el valor de una variable en una matriz ordenada que tiene un número igual de ítems a cada lado de la misma. (5 Sokal, Robert R., y F. James Rohlf. Introducción a la Bioestadística. Nueva York: Freeman, 1987. Imprimir.) Para encontrar la mediana, ponga los datos en orden de pequeños a grandes. Asignar un rango a los números. El número más pequeño tiene un rango de 1, el segundo más pequeño tiene un rango de 2, etc. El rango de la mediana se encuentra usando la fórmula 4.5.
\[Rank\ of Median = \dfrac{n + 1}{2}\]
Si n es impar, es decir, si hay un número impar de valores de datos, entonces la mediana será uno de los valores de datos. Si n es un número par, entonces la mediana será el promedio de los dos valores medios.
Los mismos datos de huracanes se utilizarán en la primera de dos demostraciones para encontrar la mediana.
| Año | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Número de huracanes | 15 | 5 | 6 | 8 | 3 | 12 | 7 |
El primer paso es crear una matriz ordenada.
| Número de huracanes | 3 | 5 | 6 | 7 | 8 | 12 | 15 |
| Rango | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
El segundo paso es encontrar el rango de la mediana usando la fórmula\(Rank\ of\ Median = \dfrac{n + 1}{2}\),\(\dfrac{7 + 1}{2} = 4\).
El tercer paso es encontrar el valor de los datos que corresponde con el rango de la mediana.
Dado que el rango de la mediana es 4 y el número correspondiente es 7 huracanes entonces el número medio es 7 huracanes.
La segunda manifestación será con el número de Huracanes del Pacífico Oriental. Dado que no hay datos para 2011, sólo se utilizarán los años 2005-2010.
| Año | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Número de huracanes | 5 | 10 | 2 | 4 | 7 | 3 |
El primer paso es crear una matriz ordenada.
| Número de huracanes | 2 | 3 | 4 | 5 | 7 | 10 |
| Rango | 1 | 2 | 3 | 4 | 5 | 6 |
El segundo paso es encontrar el rango de la mediana usando la fórmula\(Rank\ of\ Median = \dfrac{n + 1}{2}\)
\(\dfrac{6 + 1}{2} = 3.5\). Esto significa que la mediana está a medio camino entre el tercer y cuarto valores.
El tercer paso es encontrar el valor de los datos que corresponde con el rango de la mediana.
El promedio de los valores tercero y cuarto es\(\dfrac{4 + 5}{2} = 4.5\). Por lo tanto, el número medio de Pacífico Oriental
huracanes entre 2005 y 2010 es 4.5. Observe que en este caso, 4.5 no es uno de los valores de datos y ni siquiera es posible tener la mitad de un huracán, pero sigue siendo la mediana.
Una gráfica de caja es una gráfica que muestra la mediana junto con los valores más altos y más bajos y otros dos valores llamados el primer cuartil y el tercer cuartil. El primer cuartil puede considerarse como la mediana de la mitad inferior de los datos y el tercer cuartil puede considerarse como la mediana de la mitad superior de los datos.
Los Datos de Huracanes del Atlántico Norte serán utilizados para producir una parcela de caja.
El primer paso es crear una matriz ordenada.
| Número de huracanes | 3 | 5 | 6 | 7 | 8 | 12 | 15 |
| Rango | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
El segundo paso es identificar el valor más bajo, la mediana y el valor más alto.
| Más bajo | Mediana | Más alto | |||||
| Número de huracanes | 3 | 5 | 6 | 7 | 8 | 12 | 15 |
| Rango | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
El tercer paso es identificar el primer cuartil y el tercer cuartil. Esto se hace encontrando la mediana de todos los valores por debajo de la mediana y por encima de la mediana.
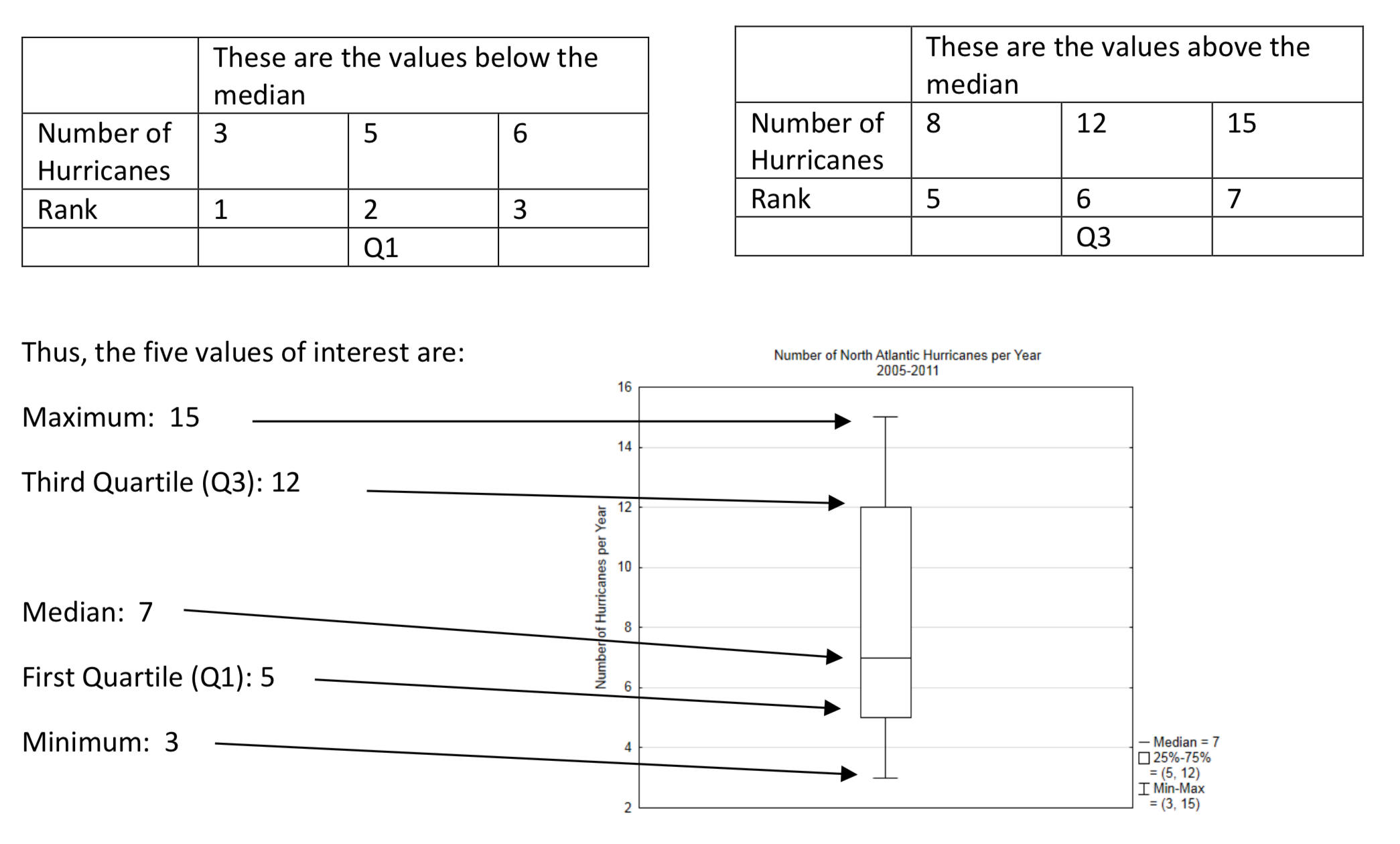
La gráfica de caja divide los datos en 4 grupos. Muestra cómo se distribuyen los datos dentro de cada grupo.
Al graficar datos cuantitativos, ¿es mejor usar un histograma o gráfica de caja? Compara las siguientes gráficas que muestran una comparación del número de huracanes en cuatro áreas, Atlántico Norte, Pacífico Este, Pacífico Oeste, Océano Índico. El dato es de los años 1970 — 2010.
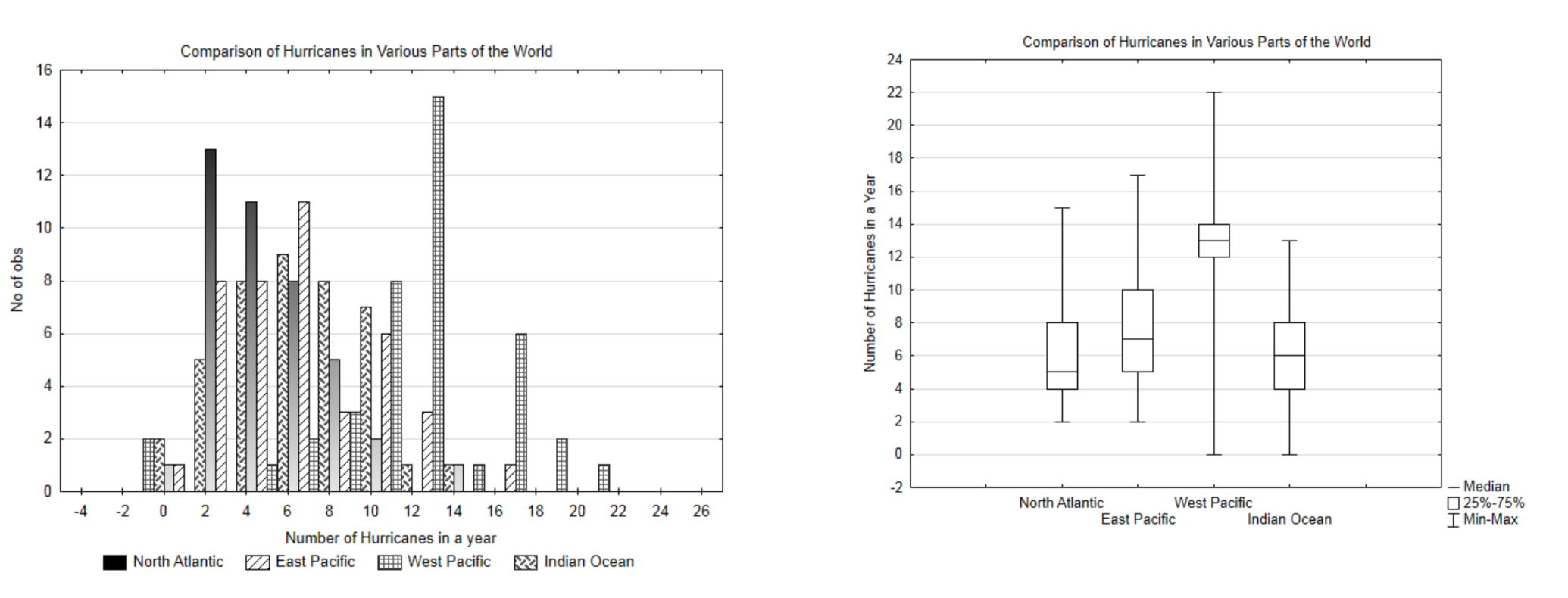
Si bien el histograma da un desglose más detallado de los datos, es muy desordenado y difícil de interpretar. Por lo tanto, a pesar de la información adicional que proporciona, el lector tiene que estudiar la gráfica con atención para entender lo que muestra. Por otro lado, la trama de caja proporciona menos información, pero es mucho más fácil hacer una comparación entre las diferentes áreas de huracanes. En general, si solo se grafica un conjunto de datos, un histograma es la mejor opción. Si hay tres o más conjuntos de datos que se están graficando, una gráfica de caja es la mejor opción. Si hay dos conjuntos de datos que se están graficando, haga tanto un histograma como una gráfica de caja y decida cuál es más efectivo para ayudar al lector a comprender los datos.
Gráficas de dispersión y correlación
Algunas preguntas de investigación resultan del deseo de encontrar una asociación entre dos variables cuantitativas. Los ejemplos incluyen brecha de riqueza (Coeficiente de Gini) /tasas de pobreza, velocidad de conducción/distancia para detenerse, capacidad de altura/salto. El objetivo es determinar la relación entre estas dos variables aleatorias y en muchos casos ver si esa relación es lineal.
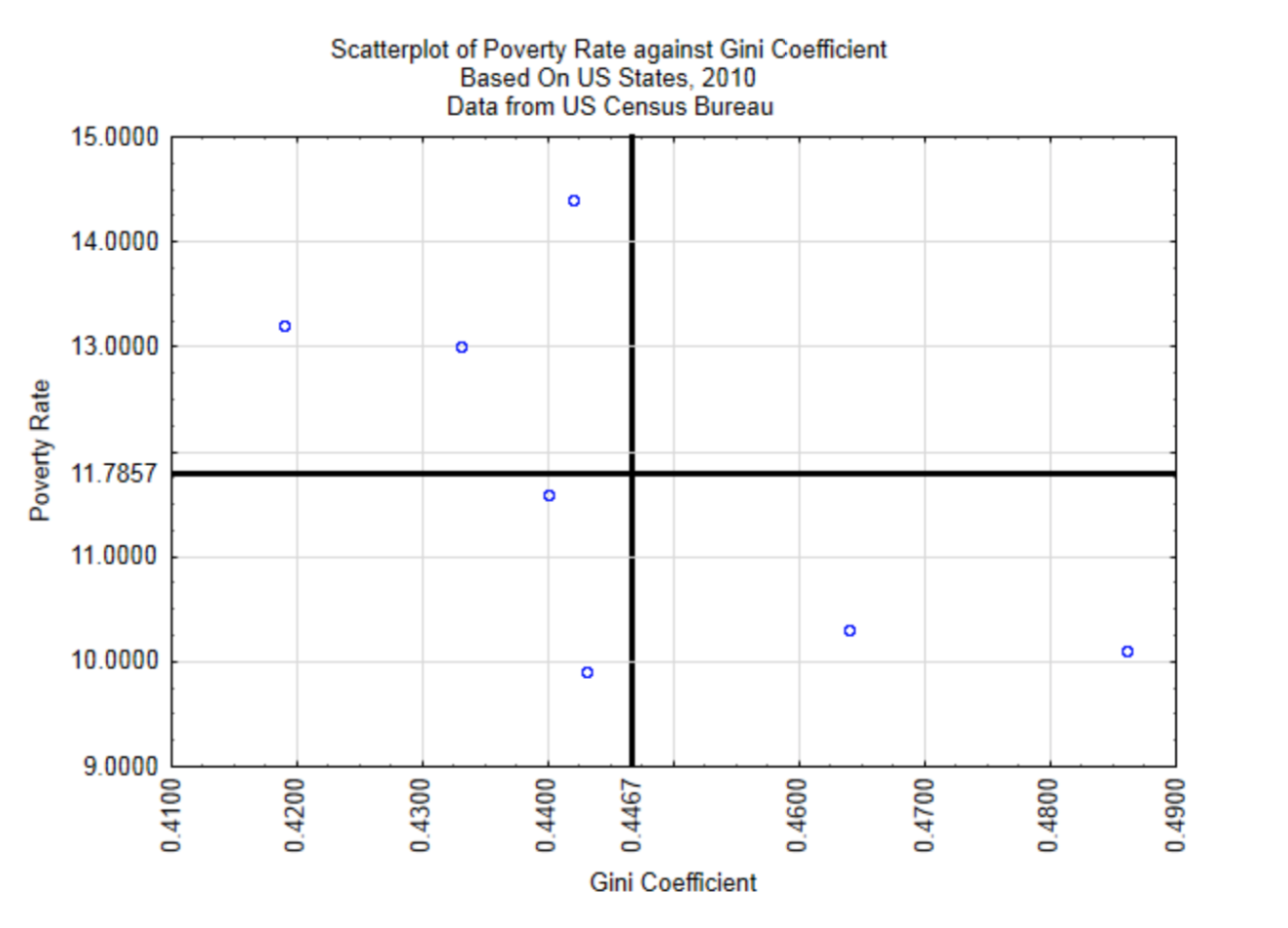
Para fines demostrativos, exploraremos la relación entre la brecha de riqueza medida por el Coeficiente de Gini y la tasa de pobreza. Las unidades serán seleccionadas aleatoriamente en Estados Unidos a partir del año 2010. Un diagrama de dispersión dará una rápida comprensión de la relación.
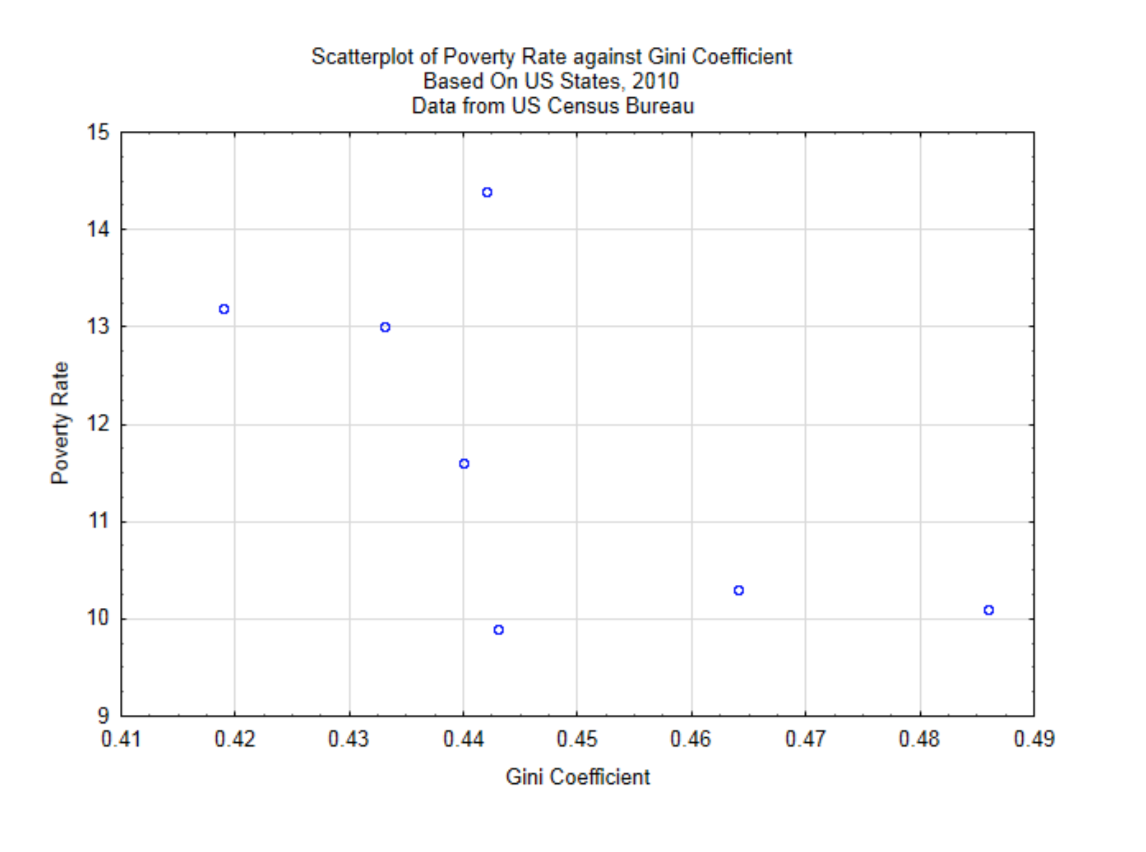
De este diagrama de dispersión se desprende que cuanto mayor es la brecha de riqueza, menor es la tasa de pobreza, aunque la relación no es fuerte ya que los puntos no parecen estar agrupados muy juntos para formar una línea recta. Para determinar la fuerza de la relación lineal entre estas variables utilizamos el Coeficiente de Correlación Producto-Momento de Pearson.
Casi siempre hay dos coeficientes de correlación de interés para nosotros. La correlación poblacional, representada con el símbolo ρ (rho), es el coeficiente de correlación que realmente nos gustaría conocer, pero que suele ser incognoscible. Hacemos hipótesis sobre ρ. La correlación muestral, representada con r, es lo que podemos encontrar a partir de una muestra y es lo que se utiliza para probar la hipótesis. La fórmula para el coeficiente de correlación muestral es:
\[r = \dfrac{\text{cov}(x, y)}{s_x s_y}\]
El numerador es la covarianza entre las dos variables, el denominador es el producto de la desviación estándar de cada variable.
La correlación siempre será un valor entre -1 y 1. Una correlación de 0 significa que no hay correlación. Una correlación de 1 significa una relación lineal directa en la que y se hace más grande a medida que x se hace más grande. Una correlación de -1 significa una relación lineal inversa en la que y se hace más pequeño a medida que x se hace más grande.
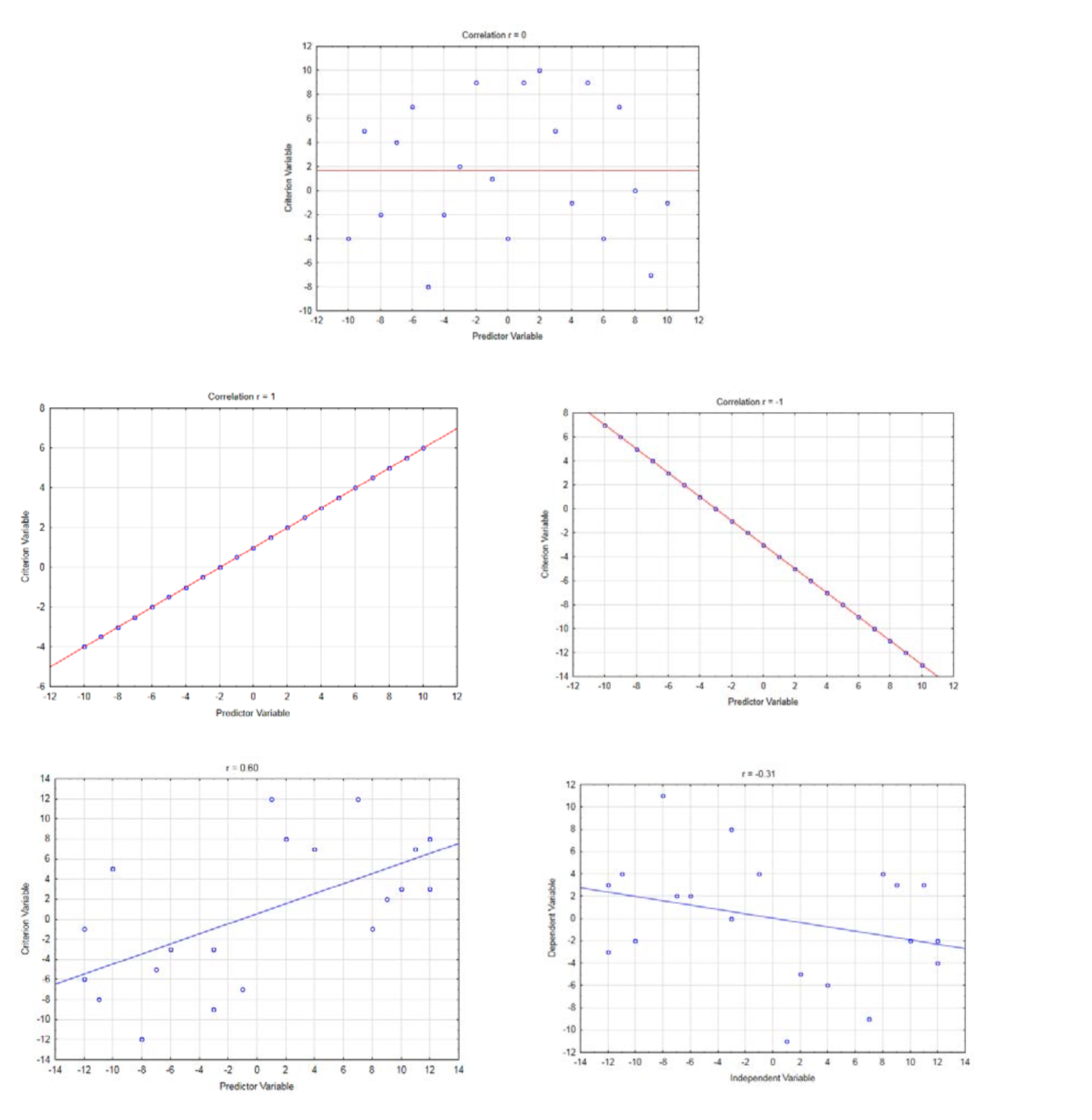
A continuación se presenta una breve explicación de la fórmula de correlación. Piense en los datos bivariados como un par ordenado (x, y). El par ordenado\((\bar{x}, \bar{y})\) es el centroide de los datos. Para estos datos, el centroide está en (0.4467, 11.7857). Esto se muestra en la gráfica a continuación.
La covarianza viene dada por la fórmula\(\text{cov}(x, y) = \dfrac{\sum (x - \bar{x})(y - \bar{y})}{n - 1}\). Muestra el producto de
la distancia que cada punto está lejos del valor promedio x y el valor promedio y. Dado que multiplicar tanto los valores x como los valores y por 10 resultaría en una covarianza 100 veces mayor de lo que producirían estos datos, sin embargo la gráfica tendría el mismo aspecto, la covarianza se estandariza dividiendo por el producto de las desviaciones estándar de x e y.
Calcular la covarianza
| (x, y) o (gini, pov) | \((x - \bar{x})\) (\(x\)- 0.4467) |
\((y - \bar{y})\) (\(y\)- 11.7857) |
\((x - \bar{x})(y - \bar{y})\) |
|---|---|---|---|
| (0.486, 10.1) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">0.0393 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">-1.6857 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.0662 |
| (0.443, 9.9) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">-0.0037 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">-1.8857 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">0.0070 |
| (0.44, 11.6) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">-0.0067 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">-0.1857 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">0.0012 |
| (0.433, 13) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">-0.0137 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">1.2143 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.0167 |
| (0.419, 13.2) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">-0.0277 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">1.4143 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.0392 |
| (0.442, 14.4) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">-0.0047 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">2.6143 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.0123 |
| (0.464, 10.3) | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">0.0173 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">-1.4857 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.0257 |
| Suma | \ ((x -\ bar {x})\) (\(x\)- 0.4467)” style="vertical-align:middle; ">0.0000 | \ ((y -\ bar {y})\) (\(y\)- 11.7857)” style="vertical-align:middle; ">0.0000 | \ ((x -\ bar {x}) (y -\ bar {y})\)” style="vertical-align:middle; ">-0.1518 |
\(\text{cov}(x, y) = \dfrac{\sum (x - \bar{x})(y - \bar{y})}{n - 1}\)
\(\text{cov}(x, y) = \dfrac{-0.1518}{7 - 1}\)
\(\text{cov}(x, y) = -0.0253\)
Calcular la desviación estándar de\(x\) y\(y\)
| (\(x\),\(y\)) o (gini, pov) | \((x - \bar{x})\) \((x - 0.4467)\) |
\((x - \bar{x})^2\) | \((y - \bar{y})\) \((y - 11.7857)\) |
\((y - \bar{y})^2\) |
|---|---|---|---|---|
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.486, 10.1) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >0.0393 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00154 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >-1.6857 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">2.84163 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.443, 9.9) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >-0.0037 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00001 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >-1.8857 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">3.55592 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.44, 11.6) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >-0.0067 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00005 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >-0.1857 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">0.03449 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.433, 13) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >-0.0137 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00019 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >1.2143 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">1.47449 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.419, 13.2) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >-0.0277 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00077 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >1.4143 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">2.00020 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.442, 14.4) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >-0.0047 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00002 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >2.6143 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">6.83449 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; "> (0.464, 10.3) | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >0.0173 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.00030 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >-1.4857 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">2.20735 |
| \ (x\),\(y\)) o (gini, pov)” style="vertical-align:middle; ">Suma | \ ((x -\ bar {x})\)\((x - 0.4467)\) "style="vertical-align:middle;" >0.0000 | \ ((x -\ bar {x}) ^2\)” style="vertical-align:middle; ">0.0029 | \ ((y -\ bar {y})\)\((y - 11.7857)\) "style="vertical-align:middle;" >0.0000 | \ ((y -\ bar {y}) ^2\)” style="vertical-align:middle; ">18.9486 |
\[ S_x = \sqrt{\dfrac{\sum (x - \bar{x})^2}{n - 1}}\]\[ S_y = \sqrt{\dfrac{\sum (y - \bar{y})^2}{n - 1}}\]\[S_x = \sqrt{\dfrac{0.0029}{7 - 1}}\]\[S_y = \sqrt{\dfrac{19.9486}{7 - 1}}\]\[S_x = 0.0219\]\[S_y = 1.777 \]
Utilice estos resultados para calcular la correlación.
\[ \begin{align*} = \dfrac{\text{cov}(x, y)}{S_x S_y} \\[4pt] &= \dfrac{-0.0253}{0.0219 \cdot 1.777} \\[4pt] &= -0.650 \end{align*}\]
Esta correlación indica que los Coeficientes de Gini más altos corresponden con menores niveles de pobreza. Si una correlación de —0.650 indica que los datos son significativos o simplemente resultados aleatorios de una población sin correlación, es cuestión para un capítulo posterior. (www.census.gov/prod/2012pubs/acsbr11-02.pdf)
Si bien es importante entender que una correlación entre variables no implica causalidad, se dibuja un diagrama de dispersión siendo una de las variables el valor x independiente, también conocido como la variable explicativa y siendo la otra el valor y dependiente, también conocido como la variable respuesta. Se utilizan los nombres explicativos y respuesta porque si existe una relación lineal entre las dos variables, la variable explicativa puede ser utilizada para predecir la variable de respuesta. Por ejemplo, uno esperaría que la velocidad de conducción influyera en la distancia de parada en lugar de la distancia de parada influyendo en la velocidad de conducción, de modo que la velocidad de conducción sería la variable explicativa y la distancia de parada sería la Sin embargo, una persona puede optar por conducir más despacio bajo ciertas condiciones debido al tiempo que podría llevarle detenerse (por ejemplo, una zona escolar) por lo que la elección de las variables explicativas y de respuesta debe ser consistente con la intención de la investigación. La precisión de la predicción se basa en la fuerza de la relación lineal. (www.census.gov/prod/2012pubs/acsbr11-01.pdf Sheskin, David J. Manual de Procedimientos Estadísticos Paramétricos y No Paramétricos. Boca Ratón: Chapman & Hall/CRC, 2000. Imprimir.)
Si se puede establecer una correlación entre la variable explicativa y la variable de respuesta, existe una de las siete posibilidades.
- Cambiar la variable x provocará un cambio en la variable y
- Cambiar la variable y provocará un cambio en la variable x
- Puede existir un bucle de retroalimentación en el que un cambio en la variable x conduzca a un cambio en la variable y que conduzca a otro cambio en la variable x, etc.
- Los cambios en ambas variables están determinados por una tercera variable
- Los cambios en ambas variables son coincidentes.
- La correlación es el resultado de valores atípicos, sin los cuales no habría correlación significativa.
- La correlación es el resultado de variables confusas.
La mejor pauta es asumir que la correlación no es causalidad, pero si crees que es en una determinada circunstancia, será necesario aportar pruebas adicionales. Una relación causal se puede establecer más fácilmente con un experimento manipulador que con un experimento observacional, ya que este último puede contener variables confusas ocultas que no se tienen en cuenta.
Calculadora TI-84
La calculadora TI-84 tiene la capacidad de encontrar rápidamente todas las estadísticas presentadas en este capítulo. Para encontrar la media aritmética, la desviación estándar y los 5 números de parcela de caja, use la tecla Stat en su calculadora. Se le presentarán tres opciones: EDITAR, CALC, PRUEBAS. Editar ya está resaltado, así que presiona la tecla enter y encontrarás tres listas etiquetadas L1, L2 y L3. También hay otras tres listas etiquetadas L4, L5, L6 que se pueden encontrar desplazándose hacia la derecha. Ingresa tus datos en una de las listas. Después de eso, presione nuevamente la tecla stat, use las flechas del cursor para desplazarse hacia la derecha hasta que Calc esté resaltado, luego presione enter. La primera opción es 1-Var Stats. Ya está resaltado, así que presiona enter, luego presiona la 2ndkey y el número correspondiente a la lista en la que se encuentran tus datos (1-6). Se le presentará la siguiente información.
\(\bar{x}\)- Media Aritmética de la Muestra
\(\sum x\)
\(\sum x^2\)
\(S_x\)- Muestra S tan dard Desviación
\(\sigma_x\)- Población S tan dard Desviación
\(n\)- tamaño de la muestra
min \(X\)- valor más bajo
\(Q\)1 - primer cuartil
Med - mediana
\(Q\)3 - tercer cuartil
max \(X\)- valor más alto
Para datos bivariados, ingrese los valores x en una lista y los valores y en otra lista diferente, cerciorándose de que estén correctamente emparejados. Utilice la tecla stat, seleccione Calc, luego seleccione 4:LinReg (ax + b). Use la segunda clave para ingresar el número de lista para la variable x seguido de una coma y luego ingrese el número de lista para la variable y. Esto proporcionará más información de la que estamos listos en este momento, pero el único valor que buscará está etiquetado como r. Si la r no es visible, deberá activar los diagnósticos de la calculadora. Esto se hace usando la\(^{\text{nd}}\) clave 2 seguida de 0 (que obtendrá el catálogo). Desplázate hacia abajo hasta DiagnostiCon y luego presiona enter dos veces.


