8.4: ¿Qué hace que un modelo sea “bueno”?

Generalmente hay dos cosas diferentes que queremos de nuestro modelo estadístico. Primero, queremos que describa bien nuestros datos; es decir, queremos que tenga el menor error posible al modelar nuestros datos. Segundo, queremos que se generalice bien a nuevos conjuntos de datos; es decir, queremos que su error sea lo más bajo posible cuando lo aplicamos a un nuevo conjunto de datos. Resulta que estas dos características a menudo pueden estar en conflicto.

Para entender esto, pensemos de dónde viene el error. Primero, puede ocurrir si nuestro modelo está equivocado; por ejemplo, si dijimos inexactamente que la altura baja con la edad en lugar de subir, entonces nuestro error será mayor de lo que sería para el modelo correcto. De igual manera, si hay un factor importante que falta en nuestro modelo, eso también aumentará nuestro error (como lo hizo cuando dejamos la edad fuera del modelo por altura). Sin embargo, el error también puede ocurrir incluso cuando el modelo es correcto, debido a la variación aleatoria en los datos, a lo que a menudo nos referimos como “error de medición” o “ruido”. A veces esto realmente se debe a un error en nuestra medición —por ejemplo, cuando las mediciones dependen de un ser humano, como usar un cronómetro para medir el tiempo transcurrido en una carrera a pie de pies. En otros casos, nuestro dispositivo de medición es altamente preciso (como una báscula digital para medir el peso corporal), pero lo que se mide se ve afectado por muchos factores diferentes que hacen que sea variable. Si conociéramos todos estos factores entonces podríamos construir un modelo más preciso, pero en realidad eso rara vez es posible.

Usemos un ejemplo para mostrar esto. En lugar de usar datos reales, generaremos algunos datos para el ejemplo usando una simulación por computadora (sobre la cual tendremos más que decir en unos pocos capítulos). Digamos que queremos entender la relación entre el contenido de alcohol en sangre (BAC) de una persona y su tiempo de reacción en un examen de manejo simulado. Podemos generar algunos datos simulados y trazar la relación (ver Panel A de la Figura 8.5).

Figura 8.5: Relación simulada entre el contenido de alcohol en sangre y el tiempo de reacción en una prueba de manejo, con el modelo lineal de mejor ajuste representado por la línea. A: relación lineal con error de medición bajo. B: relación lineal con mayor error de medición. C: Relación no lineal con error de medición bajo y modelo lineal (incorrecto)

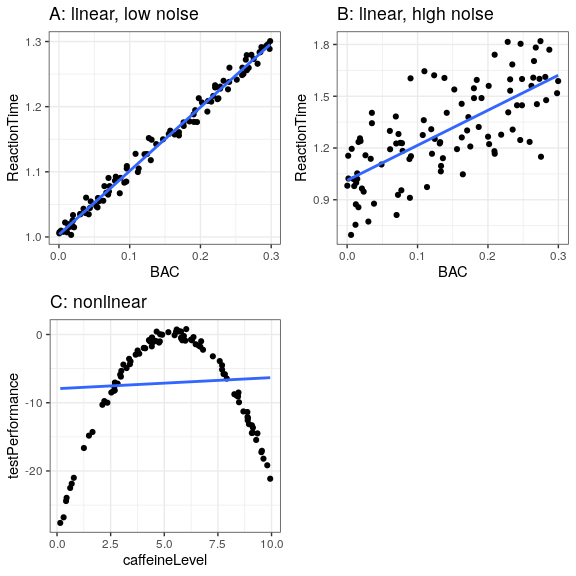
En este ejemplo, el tiempo de reacción sube sistemáticamente con el contenido de alcohol en sangre —la línea muestra el modelo que mejor se ajusta, y podemos ver que hay muy poco error, lo cual es evidente en el hecho de que todos los puntos están muy cerca de la línea.

También podríamos imaginar datos que muestran la misma relación lineal, pero tienen mucho más error, como en el Panel B de la Figura 8.5. Aquí vemos que todavía hay un aumento sistemático del tiempo de reacción con BAC, pero es mucho más variable entre los individuos.

Ambos fueron ejemplos donde el modelo lineal parece apropiado, y el error refleja el ruido en nuestra medición. El modelo lineal especifica que la relación entre dos variables sigue una línea recta. Por ejemplo, en un modelo lineal, el cambio en BAC siempre se asocia con un cambio específico en ReactionTime, independientemente del nivel de BAC.

Por otro lado, hay otras situaciones en las que el modelo lineal es incorrecto, y se incrementará el error debido a que el modelo no está debidamente especificado. Digamos que nos interesa la relación entre la ingesta de cafeína y el rendimiento en una prueba. La relación entre estimulantes como la cafeína y el rendimiento de las pruebas suele ser no lineal, es decir, no sigue una línea recta. Esto se debe a que el rendimiento aumenta con menores cantidades de cafeína (a medida que la persona se vuelve más alerta), pero luego comienza a disminuir con cantidades mayores (a medida que la persona se pone nerviosa y nerviosa). Podemos simular datos de esta forma, y luego ajustar un modelo lineal a los datos (ver Panel C de la Figura 8.5). La línea azul muestra la línea recta que mejor se ajusta a estos datos; claramente, hay un alto grado de error. Si bien existe una relación muy legal entre el rendimiento de la prueba y la ingesta de cafeína, sigue una curva más que una línea recta. El modelo lineal tiene un alto error porque es el modelo incorrecto para estos datos.