8.5: ¿Puede un modelo ser demasiado bueno?

Error suena como algo malo, y normalmente preferiremos un modelo que tenga menor error sobre uno que tenga mayor error. Sin embargo, mencionamos anteriormente que existe una tensión entre la capacidad de un modelo para ajustarse con precisión al conjunto de datos actual y su capacidad de generalizar a nuevos conjuntos de datos, ¡y resulta que el modelo con el error más bajo a menudo es mucho peor al generalizar a nuevos conjuntos de datos!

Para ver esto, volvamos a generar algunos datos para que sepamos la verdadera relación entre las variables. Vamos a crear dos conjuntos de datos simulados, que se generan exactamente de la misma manera — simplemente tienen diferente ruido aleatorio agregado a ellos.

Figura 8.6: Un ejemplo de sobreajuste. Ambos conjuntos de datos se generaron utilizando el mismo modelo, con diferentes ruidos aleatorios agregados para generar cada conjunto. El panel izquierdo muestra los datos utilizados para ajustar el modelo, con un ajuste lineal simple en azul y un ajuste complejo (polinomio de octavo orden) en rojo. En la figura se muestran los valores del error cuadrático medio (RMSE) de cada modelo; en este caso, el modelo complejo tiene un RMSE menor que el modelo simple. El panel derecho muestra el segundo conjunto de datos, con el mismo modelo superpuesto sobre él y los valores RMSE calculados utilizando el modelo obtenido del primer conjunto de datos. Aquí vemos que el modelo más simple en realidad se ajusta mejor al nuevo conjunto de datos que al modelo más complejo, que estaba sobreajustado al primer conjunto de datos.

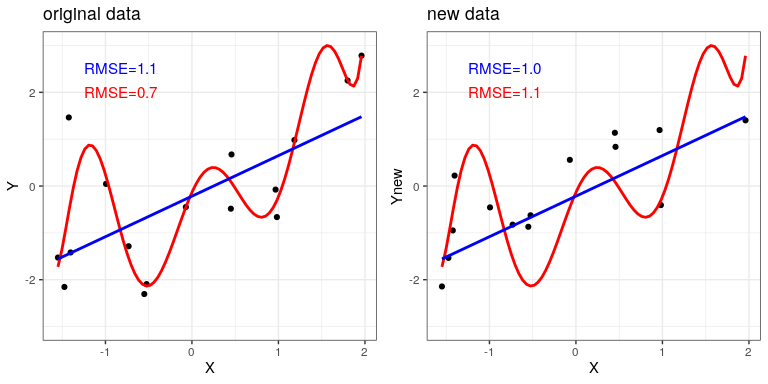
El panel izquierdo de la Figura 8.6 muestra que el modelo más complejo (en rojo) se ajusta mejor a los datos que al modelo más simple (en azul). Sin embargo, vemos lo contrario cuando se aplica el mismo modelo a un nuevo conjunto de datos generado de la misma manera —aquí vemos que el modelo más simple se ajusta mejor a los nuevos datos que al modelo más complejo. Intuitivamente, podemos ver que el modelo más complejo está fuertemente influenciado por los puntos de datos específicos en el primer conjunto de datos; dado que la posición exacta de estos puntos de datos fue impulsada por ruido aleatorio, esto lleva al modelo más complejo a encajar mal en el nuevo conjunto de datos. Este es un fenómeno al que llamamos sobreajuste. Por ahora es importante tener en cuenta que nuestro modelo fit necesita ser bueno, pero no demasiado bueno. Como dijo Albert Einstein (1933): “Apenas se puede negar que el objetivo supremo de toda teoría es hacer que los elementos básicos irreducibles sean lo más simples y pocos posibles sin tener que entregar la adecuada representación de un solo dato de experiencia”. Lo que a menudo se parafrasea como: “Todo debe ser lo más simple posible, pero no más simple”.