8.3: Modelado Estadístico- Un Ejemplo

Veamos un ejemplo de ajuste de un modelo a los datos, utilizando los datos de NHANES. En particular, intentaremos construir un modelo de la estatura de los niños en la muestra NHANES. Primero carguemos los datos y los graficemos (ver Figura 8.1).

Figura 8.1: Histograma de estatura de niños en NHANES.

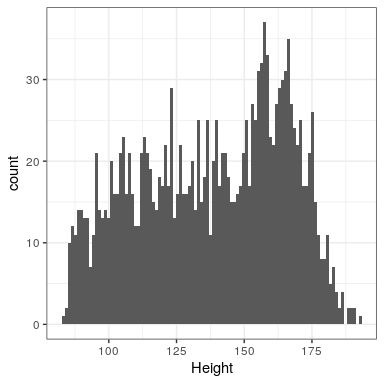
Recuerda que queremos describir los datos de la manera más simple posible sin dejar de capturar sus características importantes. ¿Cuál es el modelo más simple que podemos imaginar que aún podría capturar la esencia de los datos? ¿Qué tal el valor más común en el conjunto de datos (que llamamos el modo)?

Esto redescribe todo el conjunto de 1691 niños en términos de un solo número. Si quisiéramos predecir la altura de algún niño nuevo, entonces nuestra conjetura sería el mismo número: 166.5 centímetros.

\(\ \hat{height_i}=166.5 \)

Ponemos el símbolo hat sobre el nombre de la variable para mostrar que este es nuestro valor predicho. El error para este individuo sería entonces la diferencia entre el valor predicho (\(\ \hat{height_i}\)) y su altura real (\(\ {height_i}\)):

\(\ error_i =height_i - \hat{height_i}\)

¿Qué tan buena de modelo es esta? En general definimos la bondad de un modelo en términos del error, que representa la diferencia entre el modelo y los datos; siendo todas las cosas iguales, el modelo que produce menor error es el mejor modelo.

Lo que encontramos es que el individuo promedio tiene un error bastante grande de -28.8 centímetros. Nos gustaría tener un modelo donde el error promedio sea cero, y resulta que si usamos la media aritmética (comúnmente conocida como la media) como nuestro modelo entonces este será el caso.

La media (a menudo denotada por una barra sobre la variable, como$\ bar {X}$) es la suma de todos los valores, dividida por el número de valores. Matemáticamente, expresamos esto como:

\(\ \bar{X}=\frac{\sum_{i=1}^n x_i}{n}\)

Podemos demostrar matemáticamente que la suma de errores de la media (y por lo tanto el error promedio) es cero (ver la prueba al final del capítulo si está interesado). Dado que el error promedio es cero, este parece un mejor modelo.

Figura 8.2: Distribución de errores a partir de la media.

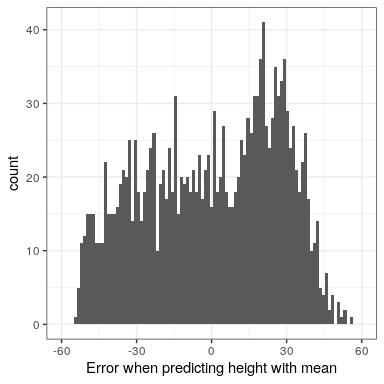
A pesar de que el promedio de errores de la media es cero, podemos ver en el histograma de la Figura 8.2 que cada individuo todavía tiene algún grado de error; algunos son positivos y otros negativos, y esos se cancelan entre sí. Por esta razón, generalmente resumimos los errores en términos de algún tipo de medida que cuenta tanto los errores positivos como los negativos como malos. Podríamos usar el valor absoluto de cada valor de error, pero es más común usar los errores al cuadrado, por razones que veremos más adelante en el curso.

Hay varias formas comunes de resumir el error cuadrado que encontrarás en varios puntos de este libro, por lo que es importante entender cómo se relacionan entre sí. Primero, podríamos simplemente sumarlos; a esto se le conoce como la suma de errores al cuadrado. La razón por la que no solemos usar esto es que su magnitud depende del número de puntos de datos, por lo que puede ser difícil de interpretar a menos que estemos viendo el mismo número de observaciones. En segundo lugar, podríamos tomar la media de los valores de error al cuadrado, que se conoce como el error medio al cuadrado (MSE). Sin embargo, debido a que los valores antes de promediar, no están en la misma escala que los datos originales; están en centímetros ². Por esta razón, también es común tomar la raíz cuadrada del MSE, a la que nos referimos como la raíz del error cuadrático medio (RMSE), de manera que el error se mide en las mismas unidades que los valores originales (en este ejemplo, centímetros).

La media tiene una cantidad bastante sustancial de error —cualquier punto de datos individual estará a unos 27 cm de la media en promedio— pero sigue siendo mucho mejor que el modo, que tiene un error promedio de unos 39 cm.

8.2.1 Mejorando nuestro modelo

¿Podemos imaginar un mejor modelo? Recuerde que estos datos son de todos los niños de la muestra NHANES, que varían de 2 a 17 años de edad. Dado este amplio rango de edad, podríamos esperar que nuestro modelo de estatura también incluya la edad. Vamos a trazar los datos para altura contra edad, para ver si esta relación realmente existe.

Figura 8.3: Altura de niños en NHANES, trazados sin modelo (A), con un modelo lineal que incluye solo edad (B) o edad y una constante (C), y con un modelo lineal que ajusta efectos separados de edad para hombres y mujeres (D).

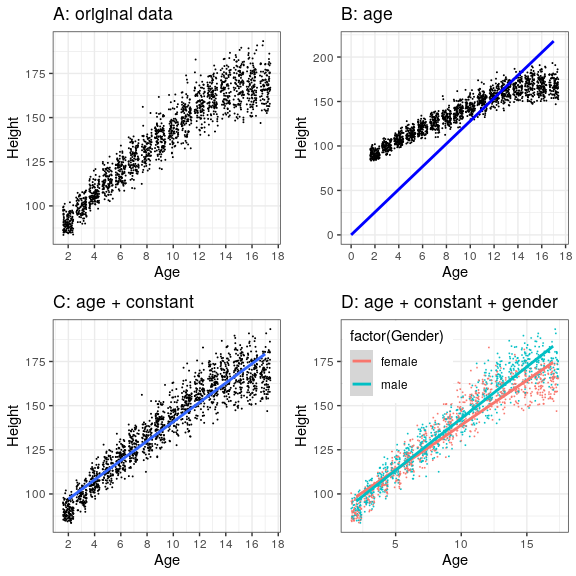
Los puntos negros en el Panel A de la Figura 8.3 muestran individuos en el conjunto de datos, y parece haber una fuerte relación entre la altura y la edad, como cabría esperar. Así, podríamos construir un modelo que relacione la estatura con la edad:

\(\ \hat{height_i}=\beta * age_i\)

donde β\ beta es un parámetro que multiplicamos por edad para obtener el menor error.

Usted puede recordar de álgebra que una línea se define de la siguiente manera:

y = pendiente ∗ x + intercepción

Si la edad es la variable X, entonces eso significa que nuestra predicción de la altura a partir de la edad será una línea con una pendiente de β y una intercepción de cero; para ver esto, trazemos la línea de mejor ajuste en azul encima de los datos (Panel B en la Figura 8.3). Algo está claramente mal con este modelo, ya que la línea no parece seguir muy bien los datos. De hecho, el RMSE para este modelo (39.16) es en realidad más alto que el modelo que solo incluye la media! El problema viene del hecho de que nuestro modelo sólo incluye la edad, lo que significa que el valor predicho de altura a partir del modelo debe tomar un valor de cero cuando la edad es cero. A pesar de que los datos no incluyen a ningún niño con una edad de cero, se requiere matemáticamente que la línea tenga un valor y de cero cuando x es cero, lo que explica por qué la línea se tira hacia abajo por debajo de los puntos de datos más jóvenes. Podemos arreglar esto incluyendo un valor constante en nuestro modelo, que básicamente representa el valor estimado de la altura cuando la edad es igual a cero; aunque una edad de cero no es plausible en este conjunto de datos, este es un truco matemático que permitirá al modelo dar cuenta de la magnitud general de los datos. El modelo es:

\(\ \hat{height_i}=constant + \beta * age_i\)

donde constante es un valor constante agregado a la predicción para cada individuo; también llamamos a la intercepción, ya que se mapea sobre la intercepción en la ecuación para una línea. Más adelante aprenderemos cómo es que realmente calculamos estos valores para un conjunto de datos en particular; por ahora, usaremos la función lm () en R para calcular los valores de la constante y β que nos dan el menor error para estos datos particulares. El Panel C en la Figura 8.3 muestra este modelo aplicado a los datos de NHANES, donde vemos que la línea coincide con los datos mucho mejor que el que no tiene una constante.

Nuestro error es mucho menor usando este modelo — sólo 8.36 centímetros en promedio. ¿Se te ocurren otras variables que también podrían estar relacionadas con la altura? ¿Qué pasa con el género? En el Panel D de la Figura 8.3 se trazan los datos con líneas ajustadas por separado para machos y hembras. De la trama, parece que hay una diferencia entre machos y hembras, pero es relativamente pequeña y solo emerge después de la edad de la pubertad. Estimemos este modelo y veamos cómo se ven los errores. En la Figura 8.4 trazamos los valores de error cuadrático medio de raíz en los diferentes modelos. De esto vemos que la modelo se puso un poco mejor yendo de modo en media, mucho mejor yendo de media a media+edad, y solo muy ligeramente mejor al incluir también el género.

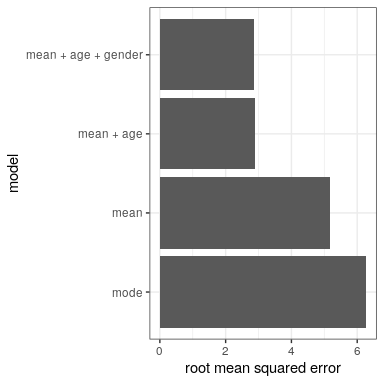Figura 8.4: Error cuadrático medio trazado para cada uno de los modelos probados anteriormente.