8.6: El modelo más simple- La media

Última actualización
Guardar como PDF

Page ID: 150840

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ya nos hemos encontrado con la media (o promedio), y de hecho la mayoría de la gente conoce el promedio aunque nunca hayan tomado una clase de estadística. Se usa comúnmente para describir lo que llamamos la “tendencia central” de un conjunto de datos, es decir, ¿en qué valor se centran los datos? La mayoría de la gente no piensa en computar una media como ajustar un modelo a los datos. Sin embargo, eso es exactamente lo que estamos haciendo cuando calculamos la media.

Ya hemos visto la fórmula para computar la media de una muestra de datos:

\(\ \bar{X}=\frac{{\sum_{i=1}^n}x_i}{n}\)

Obsérvese que dije que esta fórmula fue específicamente para una muestra de datos, que es un conjunto de puntos de datos seleccionados de una población mayor. Utilizando una muestra, deseamos caracterizar a una población mayor, el conjunto completo de individuos que nos interesan. Por ejemplo, si somos encuestadores políticos, nuestra población de interés podría ser todos votantes registrados, mientras que nuestra muestra podría incluir solo unos pocos miles de personas muestreadas de esta población. Más adelante en el curso hablaremos con más detalle sobre el muestreo, pero por ahora el punto importante es que a los estadísticos generalmente les gusta usar diferentes símbolos para diferenciar estadísticas que describen valores para una muestra de parámetros que describen el verdadero valores para una población; en este caso, la fórmula para la media poblacional (denotada como μ) es:

\(\ \mu=\frac{\sum_{i=1}^Nx_i}{N}\)

donde N es el tamaño de toda la población.

Ya hemos visto que la media es la estadística sumaria que está garantizada para darnos un error medio de cero. La media también tiene otra característica: Es la estadística resumida que tiene el menor valor posible para la suma de errores al cuadrado (SSE). En estadística, nos referimos a esto como ser el “mejor” estimador. Podríamos probarlo matemáticamente, pero en cambio lo demostraremos gráficamente en la Figura 8.7.

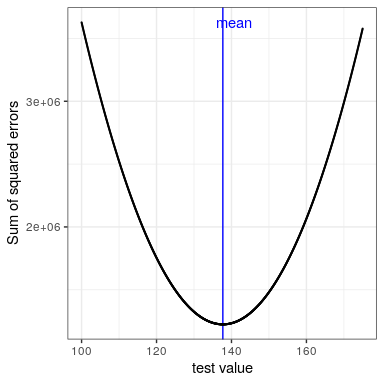
Demostración de la media como el estadístico que minimiza la suma de errores cuadrados. Usando los datos de altura del niño NHANES, calculamos la media (denotada por la barra azul). Luego, probamos un rango de otros valores, y para cada uno calculamos la suma de errores cuadrados para cada punto de datos a partir de ese valor, los cuales son denotados por la curva negra. Vemos que la media cae al mínimo de la parcela de error cuadrado. — Figura 8.7: Demostración de la media como estadística que minimiza la suma de errores cuadrados. Usando los datos de altura del niño NHANES, calculamos la media (denotada por la barra azul). Luego, probamos un rango de otros valores, y para cada uno calculamos la suma de errores cuadrados para cada punto de datos a partir de ese valor, los cuales son denotados por la curva negra. Vemos que la media cae al mínimo de la parcela de error cuadrado.

Esta minimización de SSE es una buena característica, y es por eso que la media es la estadística más utilizada para resumir datos. Sin embargo, la media también tiene un lado oscuro. Digamos que cinco personas están en un bar, y examinamos los ingresos de cada persona:

Cuadro 8.1: Ingresos para nuestros cinco clientes de bar
ingresos	persona
48000	Joe
64000	Karen
58000	Mark
72000	Andrea
66000	Pat

La media (61600.00) parece ser un resumen bastante bueno de los ingresos de esas cinco personas. Ahora veamos qué pasa si Beyoncé Knowles entra al bar:

Cuadro 8.2: Ingresos para nuestros cinco clientes de bar más Beyoncé Knowles.
ingresos	persona
4.8e+04	Joe
6.4e+04	Karen
5.8e+04	Mark
7.2e+04	Andrea
6.6e+04	Pat
5.4e+07	Beyonce

La media es ahora de casi 10 millones de dólares, lo que no es realmente representativo de ninguna de las personas en el bar —en particular, está fuertemente impulsada por el valor periférico de Beyoncé. En general, la media es altamente sensible a valores extremos, razón por la cual siempre es importante asegurarse de que no haya valores extremos al usar la media para resumir datos.

8.5.1 La mediana

Si queremos resumir los datos de una manera que sea menos sensible a los valores atípicos, podemos usar otro estadístico llamado la mediana. Si tuviéramos que ordenar todos los valores en orden de su magnitud, entonces la mediana es el valor en el medio. Si hay un número par de valores entonces habrá dos valores empatados para el lugar medio, en cuyo caso tomamos la media (es decir, el punto medio) de esos dos números.

Veamos un ejemplo. Digamos que queremos resumir los siguientes valores:

8  6  3 14 12  7  6  4  9

Si ordenamos esos valores:

3  4  6  6  7  8  9 12 14

Entonces la mediana es el valor medio —en este caso, el quinto de los 9 valores.

Mientras que la media minimiza la suma de errores cuadrados, la mediana minimiza una cantidad ligeramente diferente: La suma de errores absolutos. Esto explica por qué es menos sensible a los valores atípicos —la cuadratura va a exacerbar el efecto de grandes errores en comparación con tomar el valor absoluto. Esto lo podemos ver en el caso del ejemplo de ingresos: La mediana es mucho más representativa del grupo en su conjunto, y menos sensible al único valor atípico grande.

Cuadro 8.3: Resumen de estadísticas de ingresos tras la llegada de Beyoncé Knowles.
Estadística	Valor
Media	9051333
Mediana	65000

Ante esto, ¿por qué usaríamos alguna vez la media? Como veremos en un capítulo posterior, la media es el “mejor” estimador en el sentido de que variará menos de una muestra a otra en comparación con otros estimadores. Depende de nosotros decidir si eso vale la pena la sensibilidad a posibles valores atípicos: las estadísticas tienen que ver con las compensaciones.