10.5: ¿Cómo determinamos las probabilidades?
- Page ID
- 150537
Ahora que sabemos lo que es una probabilidad, ¿cómo averiguamos realmente cuál es la probabilidad para cualquier evento en particular?
Digamos que te pregunté cuál era la probabilidad de que los Beatles hubieran tenido igual éxito si no hubieran reemplazado a su baterista original Pete Best por Ringo Starr en 1962. Definiremos “éxito” en términos del número de éxitos número uno en el Billboard Hot 100 (al que nos referimos como N hits); los Beatles tuvieron 20 de esos éxitos número uno, por lo que el espacio de muestra es {N hits <20, N hits ≥20}. En realidad no podemos hacer el experimento para encontrar el resultado. No obstante, la mayoría de las personas con conocimiento de los Beatles estarían dispuestas a al menos ofrecer una conjetura sobre la probabilidad de este evento. En muchos casos el conocimiento y/o opinión personal es la única guía que tenemos para determinar la probabilidad de un evento, pero esto no es muy satisfactorio científicamente.
10.2.2 Frecuencia empírica
Otra forma de determinar la probabilidad de un evento es hacer el experimento muchas veces y contar con qué frecuencia ocurre cada evento. A partir de la frecuencia relativa de los diferentes resultados, podemos calcular la probabilidad de cada uno. Por ejemplo, digamos que nos interesa conocer la probabilidad de lluvia en San Francisco. Primero tenemos que definir el experimento —digamos que veremos los datos del Servicio Meteorológico Nacional de cada día en 2017 y determinaremos si hubo alguna lluvia en la estación meteorológica del centro de San Francisco.
| Número de días lluviosos | Número de días medidos | P (lluvia) |
|---|---|---|
| 73 | 365 | 0.2 |
| Según estos datos | , en 2017 hubo lluvia | y días. Para calcular la probabilidad de lluvia en San Francisco, simplemente dividimos el número de días lluviosos por el número de días contados (365), dando P (lluvia en SF en 2017) =. |
¿Cómo sabemos que la probabilidad empírica nos da el número correcto? La respuesta a esta pregunta proviene de la ley de los números grandes, lo que demuestra que la probabilidad empírica se acercará a la probabilidad verdadera a medida que aumente el tamaño de la muestra. Esto lo podemos ver simulando un gran número de volteos de monedas, y observando nuestra estimación de la probabilidad de cabezas después de cada volteo. Pasaremos más tiempo discutiendo la simulación en un capítulo posterior; por ahora, solo supongamos que tenemos una forma computacional de generar un resultado aleatorio para cada volteo de moneda.
El panel izquierdo de la Figura 10.1 muestra que a medida que aumenta el número de muestras (es decir, ensayos de volteo de monedas), la probabilidad estimada de cabezas converge en el valor verdadero de 0.5. Sin embargo, tenga en cuenta que las estimaciones pueden estar muy alejadas del valor verdadero cuando los tamaños de muestra son pequeños. Un ejemplo real de esto se vio en las elecciones especiales de 2017 para el Senado de Estados Unidos en Georgia, que enfrentaron al republicano Roy Moore contra el demócrata Doug Jones. El panel derecho de la Figura 10.1 muestra el monto relativo de la votación reportada para cada uno de los candidatos en el transcurso de la noche, ya que se contabilizaron un número creciente de boletas electorales. Temprano en la noche los recuentos de votos fueron especialmente volátiles, pasando de una gran ventaja inicial para Jones a un largo periodo en el que Moore tenía la ventaja, hasta que finalmente Jones tomó la delantera para ganar la carrera.
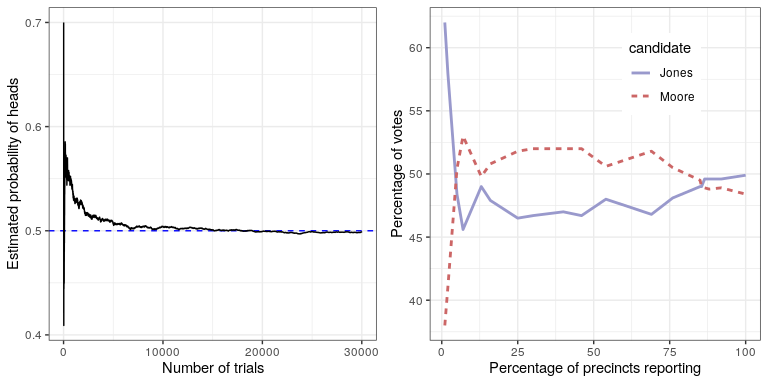
Estos dos ejemplos muestran que si bien las muestras grandes convergerán en última instancia sobre la probabilidad verdadera, los resultados con muestras pequeñas pueden estar muy lejos. Desafortunadamente, muchas personas olvidan esto y sobreinterpretan los resultados de muestras pequeñas. Esto fue referido como la ley de los números pequeños por los psicólogos Danny Kahneman y Amos Tversky, quienes demostraron que las personas (incluso investigadores capacitados) a menudo se comportan como si la ley de los grandes números se aplicara incluso a muestras pequeñas, dando demasiada crédito a los resultados de pequeños conjuntos de datos. Veremos ejemplos a lo largo del transcurso de lo inestables que pueden ser los resultados estadísticos cuando se generan a partir de muestras pequeñas.
10.2.3 Probabilidad clásica
Es poco probable que alguno de nosotros haya volteado alguna vez una moneda decenas de miles de veces, pero no obstante estamos dispuestos a creer que la probabilidad de voltear cabezas es de 0.5. Esto refleja el uso de otro enfoque más para calcular las probabilidades, a la que nos referimos como probabilidad clásica. En este enfoque, calculamos la probabilidad directamente con base en nuestro conocimiento de la situación.
La probabilidad clásica surgió del estudio de juegos de azar como dados y cartas. Un ejemplo famoso surgió de un problema que encontró un jugador francés que se llamaba Chevalier de Méré. de Méré jugó dos juegos de dados diferentes: En el primero apostó por la posibilidad de al menos un seis en cuatro tiradas de un dado de seis caras, mientras que en el segundo apostó a la oportunidad de al menos un doble-seis en 24 rollos de dos dados. Esperaba ganar dinero en ambas apuestas, pero descubrió que si bien en promedio ganó dinero en la primera apuesta, en realidad perdió dinero en promedio cuando jugó la segunda apuesta muchas veces. Para entender esto recurrió a su amigo, el matemático Blaise Pascal, quien ahora es reconocido como uno de los fundadores de la teoría de la probabilidad.
¿Cómo podemos entender esta pregunta usando la teoría de la probabilidad? En la probabilidad clásica, comenzamos con la suposición de que todos los eventos elementales en el espacio muestral son igualmente probables; es decir, cuando se rueda un dado, es igualmente probable que ocurra cada uno de los posibles resultados ({1,2,3,4,5,6}). (¡No se permiten dados cargados!) Ante esto, podemos calcular la probabilidad de cualquier resultado individual como uno dividido por el número de resultados posibles:
\(\ P(outcome_i)=\frac{1}{number\ of\ possible\ outcomes}\)
Para el dado de seis lados, la probabilidad de cada resultado individual es 1/6.
Esto es agradable, pero de Méré estaba interesado en eventos más complejos, como lo que sucede en múltiples tiradas de dados. ¿Cómo calculamos la probabilidad de un evento complejo (que es una unión de eventos individuales), como rodar uno en el primer o el segundo lanzamiento?
Representamos la unión de eventos matemáticamente usando el símbolo: por ejemplo, si la probabilidad de rodar un uno en el primer lanzamiento se conoce como P (Rol1 throw1) y la probabilidad de rodar uno en el segundo lanzamiento es P (Rol1 throw2), entonces la unión es referido como P (Rollo1 throw1 Rollo1 throw2).
de Méré pensó (incorrectamente, como veremos a continuación) que simplemente podría sumar las probabilidades de los eventos individuales para calcular la probabilidad del evento combinado, lo que significa que la probabilidad de rodar uno en la primera o segunda tirada se calcularía de la siguiente manera:
\(P\left(\text {Roll} 1_{\text {throw1}}\right)=1 / 6\)
\(P\left(\text {Roll} 1_{\text {throw2}}\right)=1 / 6\)
\(\ deMéré ^{\prime}s\ error: \)
\(P\left(\text {Roll } 1_{\text {throw1}} \cup \text {Roll }_{t \text {throw2}}\right)=P\left(\text {Roll } 1_{\text {throw1}}\right)+P\left(\text {Roll } 1_{\text {throw2}}\right)=1 / 6+1 / 6=1 / 3\)
de Méré razonó con base en esto que la probabilidad de al menos un seis en cuatro rollos era la suma de las probabilidades en cada uno de los lanzamientos individuales:\(\ 4 * \frac{1}{6}=\frac{2}{3}\). De igual manera, razonó que dado que la probabilidad de un doble-seis en tiradas de dados es 1/36, entonces la probabilidad de al menos un doble-seis en 24 tiradas de dos dados sería\(\ 24 * \frac{1}{36}=\frac{2}{3}\). Sin embargo, si bien consistentemente ganó dinero en la primera apuesta, perdió dinero en la segunda apuesta. ¿Qué da?
Para entender el error de Méré, necesitamos introducir algunas de las reglas de la teoría de la probabilidad. El primero es la regla de la resta, que dice que la probabilidad de que algún evento A no ocurra es uno menos la probabilidad de que ocurra el evento:
P (¬A) =1−P (A)
donde ¬A significa “no A”. Esta regla deriva directamente de los axiomas que discutimos anteriormente; debido a que A y ¬A son los únicos resultados posibles, entonces su probabilidad total debe sumar a 1. Por ejemplo, si la probabilidad de rodar un uno en un solo tiro es\(\ \frac{1}{6}\), entonces la probabilidad de rodar cualquier cosa que no sea uno es\(\ \frac{5}{6}\).
Una segunda regla nos dice cómo calcular la probabilidad de un evento conjunto —es decir, la probabilidad de que ocurran ambos eventos. Nos referimos a esto como una intersección, que se significa por el símbolo; así, P (AB) significa la probabilidad de que se produzcan tanto A como B.
Esta versión de la regla nos dice cómo calcular esta cantidad en el caso especial cuando los dos eventos son independientes el uno del otro; luego aprenderemos exactamente lo que significa el concepto de independencia, pero por ahora solo podemos dar por sentado que los dos lanzamientos de troqueles son eventos independientes. Calculamos la probabilidad de la unión de dos eventos independientes simplemente multiplicando las probabilidades de los eventos individuales:
P (AB) =P (A) *P (B) si y solo si A y B son independientes
Así, la probabilidad de lanzar un seis en ambos rollos es\(\ \frac{1}{6} * \frac{1}{6} = \frac{1}{36}\)
La tercera regla nos dice cómo sumar probabilidades -y es aquí donde vemos la fuente del error de Méré-. La regla de suma nos dice que para obtener la probabilidad de que ocurra cualquiera de dos eventos, sumamos las probabilidades individuales, pero luego restamos la probabilidad de que ambos ocurran juntos:
P (AB) =P (A) +P (B) −P (AB)
En cierto sentido, esto nos impide contar esas instancias dos veces, y eso es lo que distingue a la regla del cálculo incorrecto de Méré. Digamos que queremos encontrar la probabilidad de rodar 6 en cualquiera de los dos lanzamientos. De acuerdo con nuestras reglas:
\(P\left(\text {Roll } 1_{\text {throw1 }} \cup \text { Roll } 1_{\text {throw } 2}\right)=P\left(\text {Roll } 1_{\text {throw1 }}\right)+P\left(\text {Roll } 1_{\text {throw } 2}\right)-P\left(\text {Roll }_{\text {throw } 1} \cap \text {Roll }_{\text {throw } 2}\right)\)
\ (\ =\ frac {1} {6} +\ frac {1} {6} -\ frac {1} {36} =\ frac {11} {36}
\)
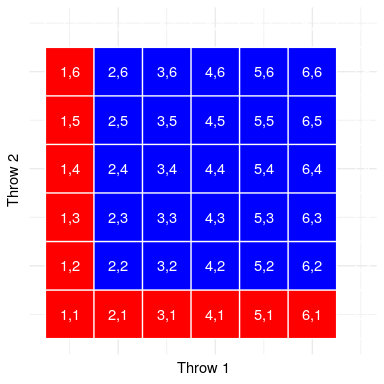
Usemos una representación gráfica para obtener una visión diferente de esta regla. La Figura 10.2 muestra una matriz que representa todas las combinaciones posibles de resultados a través de dos lanzamientos, y resalta las celdas que involucran uno en el primer o segundo lanzamiento. Si cuentas las celdas en azul claro verás que hay 11 celdas de este tipo. Esto demuestra por qué la regla de la suma da una respuesta diferente a la de de Méré; si simplemente fuéramos a sumar las probabilidades para los dos tiros como lo hizo él, entonces contaríamos (1,1) hacia ambos, cuando en realidad solo debería contarse una vez.
10.2.4 Resolviendo el problema de Méré
Blaise Pascal utilizó las reglas de probabilidad para llegar a una solución al problema de Méré. Primero, se dio cuenta de que calcular la probabilidad de al menos un evento a partir de una combinación era complicado, mientras que calcular la probabilidad de que algo no ocurra a través de varios eventos es relativamente fácil, es solo el producto de las probabilidades de los eventos individuales. Por lo tanto, en lugar de calcular la probabilidad de al menos un seis en cuatro rollos, en su lugar computó la probabilidad de no seis en todos los rollos:
\(P(\text { no sixes in four rolls })=\frac{5}{6} * \frac{5}{6} * \frac{5}{6} * \frac{5}{6}=\left(\frac{5}{6}\right)^{4}=0.482\)
Luego utilizó el hecho de que la probabilidad de no seis en cuatro rollos es el complemento de al menos un seis en cuatro rollos (así deben sumar a uno), y utilizó la regla de resta para calcular la probabilidad de interés:
\(P(\text { at least one six in four rolls })=1-\left(\frac{5}{6}\right)^{4}=0.517\)
La apuesta de Méré de que lanzaría al menos un seis en cuatro tiradas tiene una probabilidad mayor a 0.5, explicando por qué de Méré ganó dinero en esta apuesta en promedio.
Pero ¿qué pasa con la segunda apuesta de Méré? Pascal utilizó el mismo truco:
\(P(\text { no double six in } 24 \text { rolls })=\left(\frac{35}{36}\right)^{24}=0.509\)
\(P(\text { at least one double } \operatorname{six} \text { in } 24 \text { rolls })=1-\left(\frac{35}{36}\right)^{24}=0.491\)
La probabilidad de este resultado estuvo ligeramente por debajo de 0.5, mostrando por qué de Méré perdió dinero en promedio en esta apuesta.


