12.4: El Teorema del Límite Central

Última actualización
Guardar como PDF

Page ID: 150490

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El Teorema del Límite Central nos dice que a medida que los tamaños de muestra se hacen más grandes, la distribución muestral de la media se distribuirá normalmente, aunque los datos dentro de cada muestra no se distribuyan normalmente.

Esto lo podemos ver en datos reales. Trabajemos con la variable AlcoholYear en la distribución NHANES, que está muy sesgada, como se muestra en el panel izquierdo de la Figura?? . Esta distribución es, a falta de una palabra mejor, funky —y definitivamente no se distribuye normalmente. Ahora veamos la distribución muestral de la media para esta variable. La Figura 12.2 muestra la distribución de muestreo para esta variable, la cual se obtiene al extraer repetidamente muestras de tamaño 50 del conjunto de datos NHANES y tomar la media. A pesar de la clara no normalidad de los datos originales, la distribución muestral es notablemente cercana a la normal.

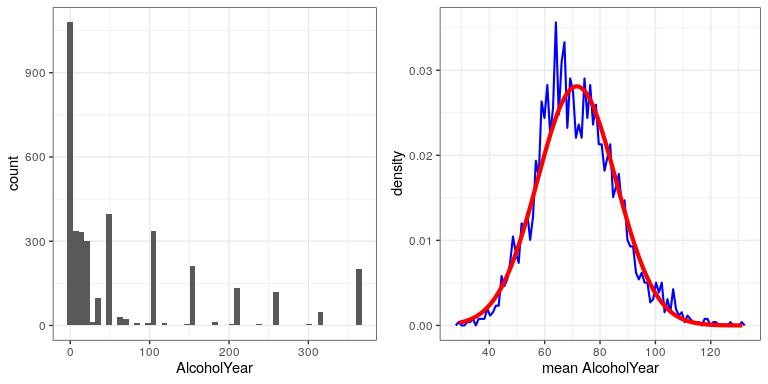
Figura 12.2: Izquierda: Distribución de la variable alcoholAño en el conjunto de datos NHANES, que refleja el número de días que el individuo bebió en un año. Derecha: La distribución muestral de la media para AlcoholYear en el conjunto de datos NHANES, obtenida dibujando muestras repetidas de tamaño 50, en azul. La distribución normal con la misma media y desviación estándar se muestra en rojo.

El Teorema del Límite Central es importante para la estadística porque nos permite asumir con seguridad que la distribución muestral de la media será normal en la mayoría de los casos. Esto significa que podemos aprovechar técnicas estadísticas que asumen una distribución normal, como veremos en la siguiente sección.