14.5: Usando Simulación para Estadísticas- El Bootstrap

Última actualización
Guardar como PDF

Page ID: 150566

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hasta ahora hemos utilizado la simulación para demostrar principios estadísticos, pero también podemos usar la simulación para responder preguntas estadísticas reales. En esta sección presentaremos un concepto conocido como bootstrap que nos permite utilizar la simulación para cuantificar nuestra incertidumbre sobre estimaciones estadísticas. Más adelante en el curso, veremos otros ejemplos de cómo la simulación a menudo se puede utilizar para responder preguntas estadísticas, especialmente cuando no se dispone de métodos estadísticos teóricos o cuando sus supuestos son demasiado difíciles de cumplir.

14.5.1 Computar el bootstrap

En la sección anterior, utilizamos nuestro conocimiento de la distribución muestral de la media para calcular el error estándar de la media y los intervalos de confianza. Pero, ¿y si no podemos suponer que las estimaciones se distribuyen normalmente, o no conocemos su distribución? La idea del bootstrap es utilizar los propios datos para estimar una respuesta. El nombre proviene de la idea de tirar de uno mismo por los propios bootstraps, expresando la idea de que no tenemos ninguna fuente externa de apalancamiento por lo que tenemos que confiar en los propios datos. El método bootstrap fue concebido por Bradley Efron, del Departamento de Estadística de Stanford, quien es uno de los estadísticos más influyentes del mundo.

La idea detrás del bootstrap es que muestremos repetidamente del conjunto de datos real; lo que es más importante, muestreamos con reemplazo, de tal manera que el mismo punto de datos a menudo terminará siendo representado varias veces dentro de una de las muestras. Luego calculamos nuestra estadística de interés en cada una de las muestras de bootstrap y usamos la distribución de esas estimaciones.

Empecemos por usar el bootstrap para estimar la distribución muestral de la media, de manera que podamos comparar el resultado con el error estándar de la media (SEM) que discutimos anteriormente.

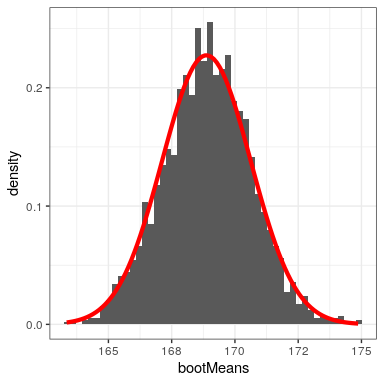
Figura 14.4: Un ejemplo de bootstrapping para calcular el error estándar de la media. El histograma muestra la distribución de medias entre las muestras bootstrap, mientras que la línea roja muestra la distribución normal basada en la media de la muestra y la desviación estándar.

La Figura 14.4 muestra que la distribución de medias a través de muestras bootstrap es bastante cercana a la estimación teórica basada en el supuesto de normalidad. También podemos usar las muestras bootstrap para calcular un intervalo de confianza para la media, simplemente calculando los cuantiles de interés a partir de la distribución de muestras bootstrap.

Tabla 14.1: Límites de confianza para distribución normal y métodos bootstrap
tipo	2.5%	97.5%
Normal	165	172
Bootstrap	165	172

Normalmente no emplearíamos el bootstrap para calcular los intervalos de confianza para la media (ya que generalmente podemos suponer que la distribución normal es apropiada para la distribución muestral de la media, siempre y cuando nuestra muestra sea lo suficientemente grande), pero este ejemplo muestra cómo el método nos da aproximadamente lo mismo resultado como el método estándar basado en la distribución normal. El bootstrap se usaría con mayor frecuencia para generar errores estándar para estimaciones de otras estadísticas donde sepamos o sospechemos que la distribución normal no es apropiada.